RBSE Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.1 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 9 Quadrilaterals Exercise 9.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 9 |
| Chapter Name | Quadrilaterals |
| Exercise | Ex 9.1 |
| Number of Questions Solved | 14 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 9 Quadrilaterals Ex 9.1
Question 1.
The angles of a quadrilateral are in (RBSESolutions.com) the ratio 3:5:9:13. Find all the angles of the quadrilateral.
Solution.
Suppose the four angles of the quadrilateral are 3x, 5x, 9x and 13x.
∴ 3x + 5x + 9x + 13x = 360°
(by angle sum property of a quadrilateral)
⇒ 30x = 360°
⇒ x = 12°
Therefore, angles of the quadrilateral are 3 x 12°, 5 x 12°, 9 x 12° and 13 x 12° i.e., 36°, 60°, 108° and 156°.
Question 2.
In a parallelogram ABCD, diagonals AC and BD intersect at O. If OA = 3 cm and OD = 2 cm, then find (RBSESolutions.com) the length of AC and BD.
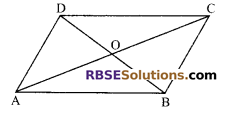
Solution.
Since, we know that diagonals of a parallelogram bisect each other
∴ AC = 2OA = 2 x 3 cm = 6 cm
and BD = 2OD = 2 x 2 cm = 4 cm.
![]()
Question 3.
Diagonals of a parallelogram are (RBSESolutions.com) mutually perpendicular. Is this statement true? Give reason for your answer.
Solution.
No, diagonals of a parallelogram bisect each other.
Question 4.
Can the angles 110°, 80°, 70° and 95° be the angles of a quadrilateral? Why or why not?
Solution.
We know that, sum of the angles of a quadrilateral is 360°.
Here 110° + 80° +70° + 95° = 355°.
∵ Sum of all the angles is not equal to 360°. So it would not be a quadrilateral.
Question 5.
Can all the four angles a quadrilateral (RBSESolutions.com) are obtuse? Give reason for your answer.
Solution.
No, if all the angles will be obtuse then sum of angles of a quadrilateral will exceed to 360°.
Question 6.
One angle of a quadrilateral is 108° and the other three angles are equal. Find the value of each of the equal angle.
Solution.
Let each of the three equal angle be x.
∴ 108° + x + x + x = 360°
(by angle sum property of a quadrilateral)
⇒ 3x + 108° = 360°
⇒ 3x = 252°
\(x=\frac { 252 }{ 3 }84\)
∴ Each equal angle is 84°.
Question 7.
ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45°, then find (RBSESolutions.com) the values of the angles C and D.
Solution.
∵ AB || DC
∴ ∠A + ∠D = 180°
(sum of the interior angle on the same side of a transversal is always 180°)
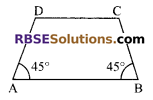
45 + ∠D = 180°
⇒ ∠D = 135°
Similarly ∠C = 135°.
Question 8.
The angle between two altitudes of a parallelogram through (RBSESolutions.com) the vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
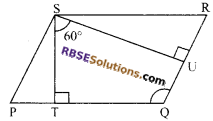
Solution.
Suppose PQRS is a parallelogram in which ∠S is obtuse.
Through the vertex S altitudes, ST and SU are drawn.
Also we have ∠TSU = 60°
Now in quadrilateral QTSU,
∠TSU + ∠STQ + ∠TQU + ∠SUQ = 360°
(sum of the angles of a quadrilateral)
or 60° + 90° + ∠TQU + 90° = 360°
⇒∠TQU = 360° – 240°
⇒∠TQU = 120°
⇒∠PQR = 120°
Now ∠PSR = ∠PQR= 120°
(opposite angles of a parallelogram)
Again ∠QPS + ∠PQR = 180°
(adjacent angles of a parallelogram are supplementary)
⇒∠QPS + 120° = 180°
⇒∠QPS = 60°
⇒∠QPS = ∠QRS = 60°
(opposite angles of a parallelogram)
Hence, angles of the parallelogram are 120°, 60°, 120° and 60°.
![]()
Question 9.
In a parallelogram ABCD, E and F are the points (RBSESolutions.com) on the diagonals AC in such a way that AE = CF then show that BFDE is a parallelogram.
Solution.
∵ ABCD is a parallelogram and E and F are the points on AC, such that AE = CF
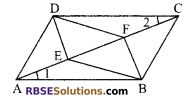
Proof: In ∆ABE and ∆CDF
AB = DC
(opposite sides of a parallelogram)
AE = CF (given)
and ∠1 = ∠2 (alt. angles)
∴ ∆ABE ≅ ∆CDF
(by SAS property)
⇒ BE = BF (by c.p.c.t)
Similarly, ∆AED ≅ ∆BFC
(by SAS property)
DE = BF (by c.p.c.t)
⇒ BFDE is a parallelogram
Question 10.
In figure, ABCD is a parallelogram and lines AQ and CP are (RBSESolutions.com) the bisector of ∠A – ∠C respectively. Prove the APCQ is a parallelogram.
Solution.
Given: ABCD is a parallelogram in which AQ and CP are the bisectors of ∠A and ∠C.
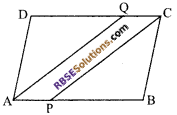
To prove: APCQ is a parallelogram.
Proof: In a parallelogram ABCD
∠A = ∠C
(opposite angles of a parallelogram)
\(\frac { 1 }{ 2 }\)∠A = \(\frac { 1 }{ 2 }\)∠C
∠PAQ = ∠PCQ
(as AQ bisect ∠A and PC bisect ∠C)
AB || CD
⇒ AP || CQ
APCQ is a parallelogram.
Hence proved.
Question 11.
In figure, ABCD and ABEF are parallelograms. Prove that CDFE is (RBSESolutions.com) also a parallelogram.
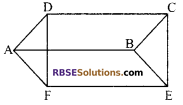
Solution.
∵ ABCD is a parallelogram
∴ AB = DC
and AB || DC …(i)
Reason: Opposite sides of a parallelogram (RBSESolutions.com) are equal and parallel. Again ABEF is a parallelogram
⇒ AB = FE
and AB || FE …(ii)
From (i) and (ii)
DC = FE and DC || FE
Therefore, CDFE is a parallelogram.
Hence proved.
Question 12.
ABCD is a parallelogram and AP and CQ are the perpendiculars from A and C on its diagonal BD, respectively. Prove that AP = CQ.
Solution.
Given: ABCD is a parallelogram in which BD is (RBSESolutions.com) diagonal and AP and CQ are drawn perpendiculars to BD from A and C respectively.
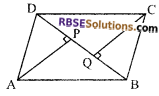
To prove: AP = CQ
Proof: Since diagonal of a parallelogram y divides its into two triangles equal in area.
∴ ar (∆ABD) = ar (∆BDC)
⇒ \(\frac { 1 }{ 2 }\) x BD x AP = \(\frac { 1 }{ 2 }\) x BD x QC
⇒ AP = QC
Hence proved.
![]()
Question 13.
In figure, ABCD is a quadrilateral in (RBSESolutions.com) which AB || CD and AD = BC, then prove that ∠A = ∠B.
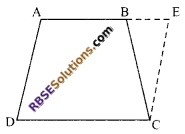
Solution.
Given: ABCD is a quadrilateral in which AB || CD and AD = BC.
Construction: Produce AB and draw a line CE parallel to AD.
To prove: ∠A = ∠B
Proof: Since AD || CE and AE cuts (RBSESolutions.com) them at A and E respectively.
∴ ∠A + ∠E=180° …(i)
Since AB || CD and AD || CE
Therefore, AECD is a parallelogram
⇒ AD = CE
⇒ BC = CE (∵ AD = BC)
Thus, in ∆BCE, we have
BC = CE (proved above)
⇒ ∠CBE = ∠CEB
(angles opposite to equal sides)
⇒ 180°-∠B = ∠E
⇒ ∠B + ∠E=180° …(ii)
From (i) and (ii), we get
∠A = ∠B
Hence proved.
Question 14.
In figure. ABCD is a parallelogram. P and Q are the mid-points (RBSESolutions.com) of opposite sides AB and DC of a parallelogram ABCD. Prove that PRQS is a parallelogram.
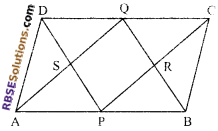
Solution.
Given: ABCD is a parallelogram. P and Q are respectively (RBSESolutions.com) the mid-points of opposite sides AB and DC of a parallelogram ABCD. AQ and DP are joined intersecting in S and CP and BQ are joined intersecting in R.
To prove: Quadrilateral PQRS is a parallelogram.
Proof: ∵ ABCD is a parallelogram.
∴ AB = DC and AB || DC
⇒ \(\frac { 1 }{ 2 }\)AB = \(\frac { 1 }{ 2 }\)DC
⇒ AP = QC and AP || QC
⇒ APCQ is a parallelogram.
Similarly. PBQD is also a parallelogram. Since in parallelogram APCQ.
AQ || PC
(opposite sides of a parallelogram)
∴ SQ || PR
Now in parallelogram PBQD
PD || BQ
∴ SP || QR
Now in quadrilateral PRQS, SQ || PR and SP || QR.
Therefore, PRQS is (RBSESolutions.com) a parallelogram.
Hence proved.
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Solutions Chapter 9 Quadrilaterals Exercise 9.1, drop a comment below and we will get back to you at the earliest.