RBSE Solutions for Class 9 Science Chapter 9 Force and Motion

RBSE Solutions for Class 9 Science Chapter 9 Force and Motion are part of RBSE Solutions for Class 9 Science. Here we have given Rajasthan Board RBSE Class 9 Science Chapter 9 Force and Motion.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 9
Subject	Science
Chapter	Chapter 9
Chapter Name	Force and Motion
Number of Questions Solved	115
Category	RBSE Solutions

Rajasthan Board RBSE Class 9 Science Chapter 9 Force and Motion

Force and Motion Textbook Questions Solved

Question 1.
Which of the following is a vector quantity?
(A) Work
(B) Time
(C) Mass
(D) Gravitational force
Answer: D

Question 2.
Two forces of 4 N and 3 N are acting on an object in opposite directions, the resultant force that will act on the object is:
(A) 5 N
(B) 7 N
(C) 1 N
(D) In between 1 N and 7 N
Answer: C

Question 3.
The rate of change of velocity is:
(A) Force
(B) Momentum
(C) Acceleration
(D) Displacement
Answer: C

Question 4.
Unit of momentum is:
(A) Newton metre
(B) Newton kg/ metre
(C) Newton metre/sec
(D) Newton metre
Answer: D

Question 5.
The velocity-time graph of a moving object with uniform velocity is:
Answer: C

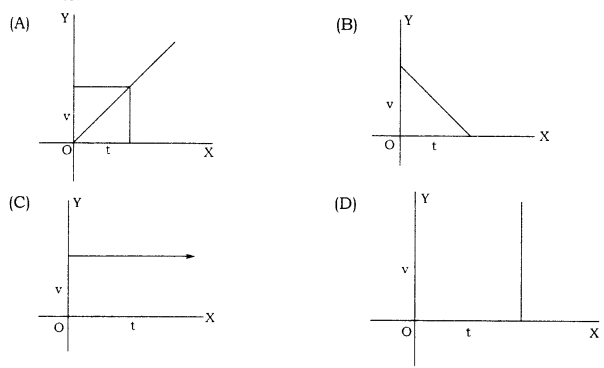
Question 6.
The momentum of a body depends on:
(A) mass of body
(B) displacement of a body
(C) time is taken in displacement
(D) all above
Answer: A

Question 7.
The relation between force (F), mass (m) and acceleration (a) is:
(A) F = ma
(B) m = aF
(C) a = mF
(D) ma = \(\cfrac { 1 }{ F } \)
Answer: A

Question 8.
Unit of Force is:
(A) kg-m-sec
(B) kg-m-sec²
(C) kg-m/sec²
(D) kg-m/sec
Answer: C

Question 9.
On accelerating a moving body:
(A) there is always an increase in its speed
(B) there is always a decrease in its speed
(C) the body will fall towards the earth
(D) there is a force acting on it always
Answer: B

Question 10.
if a body is in motion in straight line with constant momentum and if no external force act on a body then:
(A) velocity will increase
(B) velocity remain constant
(C) after some time the body will come to rest
(D) speed will increase.
Answer: B

Question 11.
The Inertia, of a body, depends on:
(A) the centre of gravity of a body
(B) mass of an object
(C) acceleration due to gravity
(D) size of an object.
Answer: B

Question 12.
A body of mass 5 kg is moving in a straight line with an acceleration of 10m/sec2. The resultant force act on a body is:
(A) 50 N
(B) 0.5 N
(C) 0
(D) 2 N
Answer: A

Question 13.
The force exerted on anybody can:
(A) change the motion of the body
(B) change the direction of motion
(C) change the size of the body
(D) all above
Answer: D

Question 14.
The weight of an object of mass 1 kg is equal to:
(A) 1 N
(B) 9.08 N
(C) 9.8 N
(D) 8.9 N
Answer: C

Question 15.
If the mass of an object is m, velocity v and acceleration a, then momentum p will be equal to:
(A) p = ma
(B) p = mv
(C) P = \(\cfrac { m }{ v } \)
(D) P= \(\cfrac { v }{ m } \)
Answer: B

Question 16.
An object cannot change the state of rest or motion, due to:
(A) it’s mass
(B) it’s weight
(C) it’s acceleration
(D) it’s inertia
Answer: D

Question 17.
On the given surface if force is made double on that surface then pressure:
(A) will become half
(B) unchanged
(C) will become doubled
(D) will become four times
Answer: C

Force and Motion Very Short Answer Type Questions

Question 18.
What will be the acceleration of an object after 10 sec which is moving with constant velocity of 40 m/s?
Answer
When an object is moving with constant velocity then change in acceleration would be zero,
i.e., u = v = 40 m/s
\(a=\cfrac { \upsilon -u }{ t } =\cfrac { 40-40 }{ 10 } =\cfrac { 0 }{ 10 } =0m/{ s }^{ 2 } \)

Question 19.
What wilt be the change in momentum of moving object of mass‘m’ and velocity u after hitting with the wall it returns back with velocity u?
Answer
Change in momentum = mu-(-mu) = 2 mu

Question 20.
A train is moving with a velocity of 120 km/h. How much distance it will cover in 30 minutes?
Answer
Velocity of train
\(= 120 km/h= \cfrac { 120km }{ 60\quad minutes } =2km/minutes \)

Question 21.
What quantity is equal to the area under the velocity-time graph and the time axis of a moving object?
Answer
The area under the velocity-time graph and the time axis of a moving object are equal to the distance travelled in the given time interval.

Question 22.
On which law the principle of the rocket is based?
Answer
The principle of the rocket is based on Newton’s third law of motion, the law of action and reaction.

Question 23.
What is the direction of the frictional force acting on a moving bicycle?
Answer
A frictional force acts in the direction opposite to the direction in which the cycle is moving, at the point of contact of wheels with the road.

Question 24.
Why does a fielder pull his arms back while trying to stop or catch a cricket ball?
Answer
In the game of cricket, a fielder stops/catches a ball by gradually pulling his hands back along with the ball. This is done to decrease the rate of change of its momentum by increasing the time.

Question 25.
Why an athlete always runs some distance before taking a long jump?
Answer
Athlete acquired the inertia of motion by running and then continues in this state so that he can jump to a longer distance.

Question 26.
Why a standing passenger was thrown in the forward direction when a running bus stops suddenly?
Answer
Passengers standing or sitting in running bus share the motion of the bus. This means the passengers in a running bus are also moving with the same speed in the same direction. When the running bus stops suddenly the lower part of the passenger’s body comes to rest, while the upper part continues to remain in motion. As a result, the passengers are thrown in the forward direction.

Question 27.
An object is moving with a constant velocity then what will be the resultant force on it?
Answer
Since the object is moving with a constant velocity, it means an acceleration of the body will be zero. So, the resultant/ net force on the object will be zero.

Question 28.
A person is standing on ice at the centre of a frozen lake. What should he do to reach the shore?
Answer
He should exert a push on the ice, (taking help if possible, of a stick or pole) backwards. As a reaction he will be pushed forward and thus slipping on the surface of the ice, he will reach the shore.

Question 29.
What is one Newton force?
Answer
One Newton is that amount of force which when act on a body of mass 1 kg produces an acceleration of 1/s².

Question 30.
What is inertia?
Answer
The property by virtue of which a body tends to oppose any change in its position of rest or of uniform motion is called inertia.

Question 31.
After applying brakes, moving car stops. In this process where is the momentum goes?
Answer
A major part of momentum goes to earth, and remaining part is transferred to molecules.

Question 32.
Before firing the bullet, find the momentum of the gun and bullet.
Answer
Zero.

Question 33.
What is thrust?
Answer
The recoil (force) due to the reaction of an action is called thrust.

Question 34.
What is the unit of relative density?
Answer
\(Relative\quad density=\cfrac { Density\quad of\quad any\quad object }{ Density\quad of\quad water } \)

Force and Motion Short Answer type Questions

Question 35.
Define the following:
(1) Displacement
(2) Velocity
(3) Acceleration.
Answer
(1) Displacement: When a body moves from one position to another, the shortest distance (straight distance) measured between initial and the final position of the moving body, in a particular direction is called displacement. It is a vector quantity,

(2) Velocity: Velocity of a body is the displacement of a body per unit time.
\(Velocity\quad =\cfrac { Displacement }{ Density\quad of\quad water } \)

(3) Acceleration: The rate of change of velocity of a body with respect to time is called its acceleration. It is denoted by ‘a’, i.e.
\(a=\cfrac { \upsilon -u }{ t } \quad =\cfrac { Final\quad Velocity-Initial\quad Velocity }{ Time\quad Taken\quad to\quad Change } \)
Its unit is m/s² in S.I system and cm/s² in C.G.S system.

Question 36.
What do you mean by uniform motion? Give one example.
Answer
A body is said to be in uniform motion, if it travels an equal distance in equal interval of time, no matter how small these time interval may be.
Example: The movement of the earth around the sun.

Question 37.
If action is always equal to the reaction, explain how a horse can pull a cart.
Answer
When a horse pulls a cart with a certain force, the cart also pulls the horse with the same force. But, in an effort to pull the cart, the horse pushes the ground backwards with his feet. To this action of the horse, the ground offers reaction. A part of this reaction from the ground balances the weight of the cart, while the other part makes the cart move in the forward direction.

Question 38.
Explain why some of the fruits may get detatched from a tree if we vigorously shake its branch.
Answer
This is due to the inertia of rest. When the branch is shaken swiftly, the branch suddenly moves a little distance, but the fruits attached to it by a slender stalk (petiole) tend to remain where they are (due to inertia). So, the stalk feels a jerk and breaks away and the fruit falls down.

Question 39.
In water/oil tankers some space is left empty at the top while filling them. Explain, why?
Answer
When a tanker full of any liquid is moved, due to the force pulling it (the action), an equal and opposite reaction acts on the liquid. So, the liquid rolls and rises up and down, for which some space is left in the tanker. Otherwise, the liquid would split out.

Question 40.
If someone jumps to the shore from a boat, the boat moves away in opposite direction. Explain why?
Answer
When a man jumps from a boat to the shore, he pushes the boat behind with his leg (action) and the boat pushes (reaction) the man in the opposite direction. Because of this, the man moves towards the shore and the boat moves away in the opposite direction. Therefore the boats are tied to the bank with a rope.

Question 41.
Two forces acting on a body always act in a pair. There is no possibility of a single force. Comment on this statement.
Answer
Forces in nature always occur between a pair of bodies. Force exerted on body A by body B is equal and opposite to the force exerted on the body B by A. i.e., Force exerted on A by
B = – Force exerted on B by A.

Question 42.
What is the difference between rolling friction and sliding friction?
Ans:

Rolling Friction	Sliding Friction
1 When the surface of one body is rolling against the surface of another body, rolling friction comes into play. 2. Rolling friction occurs due to deformation of surfaces.	1. When the surface of one body is sliding against the surface of another body, sliding friction comes into play. 2. Sliding friction occurs due to interlocking between microscopic bumps on surfaces.

Question 43.
What is the law of conservation of momentum? Explain by giving examples.
Answer
It states that the total momentum of any system of objects remains constant in the absence of any external force. According to the law of conservation of momentum, for a collision between two bodies
Total momentum before collision = Total momentum after the collision.
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
Example: When a shot is fired from a gun, the gun recoils. When the shot is fired, it leaves the barrel with a certain force. The outgoing shot causes a reaction on the gun. Thus an equal and opposite force acts on the gun and it recoils.

Question 44.
State some methods to reduce friction.
Answer
Some of the methods to reduce friction are:
(a) By polishing
(b) By using ball bearings
(c) By lubrication
(d) By streamlining

Question 45.
A car and a truck have the same linear momentum. Which one will have more speed and why?
Answer
The truck and a car have the same momentum.
i.e.,   p₁ = MV where M is mass of truck and V velocity of the truck
Similarly, p₂= mv where m is mass of the car, v is the velocity of the car Obviously mass of truck is greater than the mass of the car, so the speed of car will be more than truck in order to make p₁ = p₂

Question 46.
What are the advantages and disadvantages of friction?
Answer
Advantages of friction:

• Friction helps us in walking on the floor.
• We can not fix a nail in the wood or wall if there is no friction. It is friction which holds the nail.
• A horse cannot pull a cart unless friction furnishes him a secure foothold.
• Friction helps in applying brakes to stop a vehicle.
• Without friction, we cannot write on a paper or on a board.

Disadvantages of friction:

• It opposes the motion.
• Due to friction, noise is produced in machines.
• Due to friction, there is a loss of energy, which decreases the efficiency of an engine.
• Due to friction, engines of automobiles consumes approximately 20% excess fuel which is a money loser.
• Due to friction, we have to exert more power in machines.

Question 47.
What happens when you shake a wet piece of cloth? Explain.
Answer
When we shake a wet cloth, water droplets come off from it, because of inertia of rest. Water drops in the wet cloth were in a position of rest. When shaken, the cloth moves suddenly, but the droplets have a tendency to remain at rest owing to the property of inertia and they are detached from the cloth.

Question 48.
Why a man pulling a bucket of water from a well, suddenly fell down on breaking down of rope?
Answer
Initially, the man was pulling the rope in upwards direction. After breaking of rope, the force acting on man by the rope disappears. So, due to the disappearance of this force, he fells down. Heavier the buckets, heavier the thrust the man will feel.

Question 49.
Why do passengers jumping out of a rapidly moving vehicle, fall forward? Give reason.
Answer
A passenger travelling in a bus/train share the motion of the bus/train. Thus the passenger’s body is moving in the direction of the bus with the same speed. When the passenger jumps out of a fast-moving bus/train, his feet will come to rest on touching the ground, whereas the upper part of his body continues to move forward, due to the inertia of motion. As a result, if he does not run forward he will fall with his face in downwards direction.

Question 50.
Why does a ship make of iron float while a sheet of iron sinks?
Answer
The structure of a ship is much bigger than that of iron sheet. When a ship enters in water, it displaces a large volume of water, whereas, the weight of water displaced by an iron sheet is much higher when it enters in water than the ship. As a result, iron sheet sinks, while a ship floats on water.

Question 51.
What is the difference between density and relative density?
Answer

Density	Relative density
(a) Density is defined as mass per unit volume.	(a) The relative density of a substance is defined as the ratio of the density of the substance, to the density of water.
(b) Its unit is kg/m3.	(b) It has no unit, as it is a ratio.

Question 52.
What is Archimedes’ principle?
Answer
When an object is immersed wholly or partly in a fluid (liquid or gas), it experiences an upward force, called buoyant force which is equal to the weight of the fluid displaced by it.

Force and Motion Long Answer Type Questions

Question 53.
Explain scalar and vector quantities. Write a way to express a vector. Define unit vector.
Answer
Scalar and vector quantities: The physical quantities which have only magnitude and need no idea of direction are called scalar quantities.
For example: Speed, mass, time, length, area, volume, density, work, energy etc.

Vector quantities: There are certain quantities which require magnitude as well as direction, to express them clearly, i.e., the physical quantities which have magnitude, as well as direction, are called vector quantities.
For example: Velocity, acceleration, force, pressure etc.

Vector representation: A vector quantity is represented by a single arrow. It is written as \(\bar { AB } \). Here, length of AB is the magnitude of | \(\bar { AB } \) |.

Unit Vector
A unit vector is a vector whose magnitude is unit and direction is the direction of the vector, say \(\bar { AB } \). A unit vector is denoted by \(\hat { A } \) and it is read as A cap.
\(\bar { A } =|\bar { A } |\quad \hat { A } =\hat { A } =\frac { \bar { A } }{ |\bar { A } | } \)

Question 54.
Explain uniform and non-uniform motion. Reduce the equation of motion from velocity-time graph.
Answer
Uniform acceleration: When the change in the velocity of a moving body is the same in each second then its acceleration is said to be uniform. Such motion is said to be uniformly accelerated motion or uniform motion.

Non-Uniform acceleration: When the change in velocity of a moving body is not the same in each second then its acceleration is said to be non-uniform acceleration. Such motion is called non-uniform motion.

The equation of motions from the velocity-time graph:
The velocity-time graph for a body under uniform acceleration is shown in the figure.
Let initial velocity of the body = u
The final velocity of the body = v
Time is taken by the body = t
Acceleration of the body = a

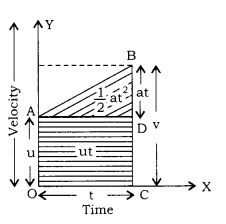
Derivation of the first equation of motion:
According to the definition,
Acceleration of a body = Rate of change of velocity i.e. slope of the velocity-time graph.
The velocity-time graph for a uniformly accelerated body is given by the straight line AB. So, acceleration of the body is equal to the slope of the line AB.

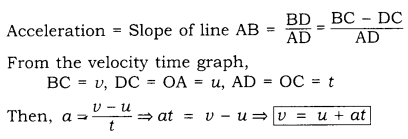
⇒ First equation of motion

Derivation of the second equation of motion
Under the uniform acceleration, from the figure, one can write
Distance travelled (s) = Area of trapezium OABC
S= Area of the triangle ABD + Area of rectangle OADC

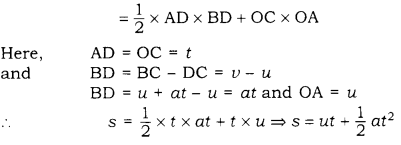
This is second equation of motion.
Derivation of third equation of motion
Distance travelled, s = Area of the trapezium OABC

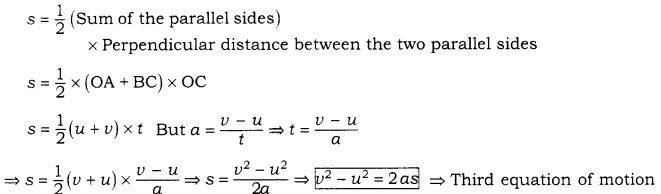
Question 55.
Define balanced and unbalanced forces. Explain with the help of figure that only unbalanced force produce motion in the body.
Answer
Balanced forces: When a number of forces acting on a body do not cause any change in its state of rest or of uniform motion along a straight line then the forces are said to be balanced forces. In other words, a body is said to be underbalanced forces when the resulting force acting on the body is zero.

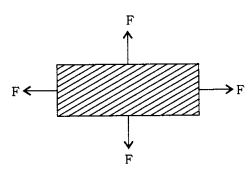
The balanced forces:

• Cannot set any stationary body into motion.
• May change the shape and size of soft objects.
• Cannot change the speed/velocity of a moving body.

Unbalanced forces:
When the resultant of all the forces acting on a body is not zero, then forces are called unbalanced forces.

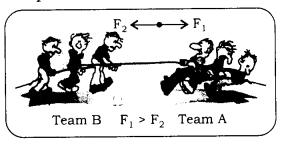
Example:

• Game of tug of war: When the forces exerted by both the teams are equal, then the rope does not move. But, if the force applied by team A is greater than team B, then the rope, as well as members of the weaker team, i.e., B, will be pulled towards A. The unbalanced force can (a) Set a stationary body in motion.
• Set a moving body at rest.
• Change the direction of motion.

Question 56.
Describe Newton’s laws of motion on the basis of daily life examples. On the basis of the second law, find the relation between force, mass and acceleration.
Answer
Newton’s first law of motion-According to this law, a body at rest or in uniform motion will continue to be in the state of rest or uniform motion unless it is compelled by an external force to change its state of rest or uniform motion.
Examples:

• An athlete runs for a certain distance before taking a long jump.
• A person sitting/standing on a bus fall back when the bus suddenly starts moving forward.
• The carpet is beaten with a stick to remove the dust particles.

The second law of motion: The acceleration produced in the body by the action of a force acting on it is directly proportional to the force and inversely proportional to the mass of the body. Mathematically, F = ma, where, F = force, m = mass of the body. In other words,
Newton’s second law of motion can be stated as:
The rate of change of momentum is equal to the force applied to the body and the change in momentum always takes place in the direction of the force.

Examples:                                                                                                                                  ‘

• A cricket player lowers his hands while catching the ball.
• A person falling on a cemented floor gets injured, but a person falling on a heap of sand does not get injured.

Third law of Motion: According to this law:
“For every action, there are an equal and opposite reaction” (Law of action and reaction) Examples:

• Gun gives a jerk to shoulder of the gunman on firing a bullet from it.
• Boatman pushes the river bank with a bamboo pole to take his boat into the river.

Question 57.
What do you mean by inertia? Illustrate with two examples.
Answer
Newton’s first law of motion defines inertia as the inherent property of a body by virtue of which it resists any change in its state of rest or of uniform motion in a straight line on its own. This law is also known as the law of inertia.
Inertia can be categorised into three types:
(a) Inertia of rest
(b) Inertia of motion
(c) Inertia of direction
Examples:
(a) The carpet is beaten with a stick to remove the dust particles. Initially, both the carpet and the dust in it are at rest. When the carpet is shaken or beaten with a stick, the carpet is set into motion. Due to the inertia of rest, the dust particle tends to remain at rest. As a result, the dust particles fall off.
(b) The passengers in a bus tend to fall back when it starts suddenly. When a passenger is sitting in a stationary bus, both the bus and the passenger are at rest. When the bus starts suddenly, the lower part of the passenger’s body starts moving forward with the bus. However, the upper part of the passenger’s body tends to remain in the position of rest, due to the inertia of rest. As a result, the passengers fall or lean backwards.

Question 58.
Define momentum. Prove that momentum before the collision is equal to the total momentum after the collision.
Answer
Momentum: The product of mass and velocity of a moving body is called momentum.
Momentum = Mass of body x Velocity.
\(\overrightarrow { p } =m\overrightarrow { v } \)

Law of conservation of momentum: The law states, in absence of external forces the momentum of the system is conserved. It means that the total momentum before the collision is equal to the total momentum after the collision.
Suppose two bodies A and B of masses m₁ and m₂ are moving in a straight line in the same direction with velocities u₁ and u₂, the velocity of the body A is more than that of B. So both the bodies will collide after some time. Velocities of the bodies A and B after collision become v₁ and v₂, respectively. The time of collision is t.

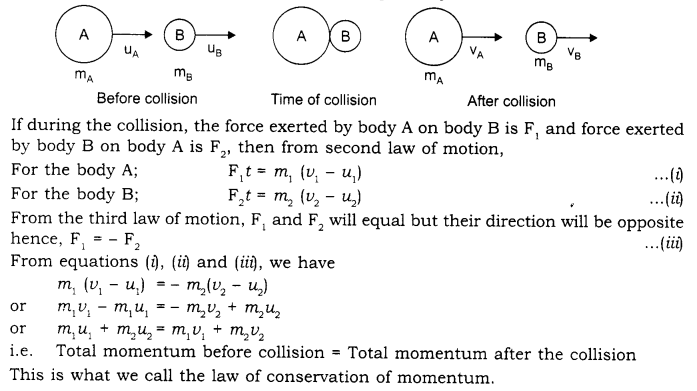
Force and Motion Additional Questions Solved

Multiple Choice Questions (MCQs)

Question 1.
Which of the following is not a scalar quantity?
(A) Time
(B) Volume
(C) Displacement
(D) Work
Answer: C

Question 2.
The horizontal straight line obtained from the distance-time graph is related to which of the following velocity?
(A) Zero velocity
(B) Constant velocity
(C) Increasing velocity
(D) Decreasing velocity
Answer: A

Question 3.
Which of the following is not a unit of force?
(A) Pound
(B) Dyne
(C) Joule
(D) Newton
Answer: D

Question 4.
A body starts with an initial velocity of 5m/s. If the acceleration of the body is 2 m/s², its velocity after 8 seconds will be:
(A) 21 m/sec
(B) 18 m/sec
(C) 10.5 m/sec
(D) 9 m/sec
Answer: A

Question 5.
The inertia of a body depends on
(A) the velocity of the body
(B) acceleration of the body
(C) the shape of the body
(D) mass of the body
Answer: D

Question 6.
The momentum of the body does not depend on-
(A) mass of the body
(B) the speed of the body
(C) acceleration of the body
(D) the velocity of the body
Answer: C

Question 7.
A moving body of mass m and velocity v after colliding from a wall returns back (rebounds) with velocity v. The change in momentum will be
(A) 2 mv
(B) mv
(C) – mv
(D) zero
Answer: A

Question 8.
Which of the following is not an example of force acting at a distance?
(A) Force of gravity
(B) Magnetic force
(C) Electrical force
(D) Frictional force
Answer: D

Question 9.
A force of 20 Newton is acting on a moving body. If the magnitude of the applied force is doubled, the acceleration of the body as compared to previous acceleration will be
(A) four times
(B) two times
(C) half
(D) one fourth
Answer: B

Question 10.
A metallic sphere having mass 2 kg is moving with a velocity of 10 m/s. The momentum of the sphere in kg metre/ sec. will be-
(A) 1/5
(B) 5
(C) 12
(D) 20
Answer: D

Question 11.
A body starts with an initial velocity of 15 m/s. If the acceleration of the body is 4 m/s², its velocity after 8 seconds will be-
(A) 47 m/sec
(B) 28 m/sec
(C) 15 m/sec
(D) 13 m/sec
Answer: A

Question 12.
The force, according to Newton’s second law of motion is”equal to
(A) Mass x Velocity
(B) Mass x Acceleration
(C) \(\cfrac { Mass }{ Acceleration } \)
(D) \(\cfrac { Mass }{ Velocity } \)
Answer: B

Question 13.
An object is moving with a uniform velocity of 9.8 m/s², its acceleration is-
(A) Zero
(B) 4.9 m/sec²
(C) 8 m/sec²
(D) 19.6 m/sec
Answer: A

Question 14.
Momentum gives the measure of
(A) mass
(B) weight
(C) velocity
(D) the quantity of motion
Answer: D

Question 15.
Internal forces
(A) are always balanced forces
(B) are unbalanced forces
(C) may or may not be balanced
(D) nothing can be said about these forces
Answer: A

Force and Motion Very Short Answer Type Questions

Question 1.
What does the odometer of an automobile measure?
Answer
An odometer measures the distance covered by the automobile in a kilometre.

Question 2.
What type of motion is shown by
(a) a point marked on the blade of a running ceiling fan?
(b) a ball dropped from a height
Answer
(a) Uniform circular motion.
(b) Uniformly accelerated linear motion.

Question 3.
The displacement of a moving object in a given interval of time is zero, would the distance travelled by the object also is zero? Justify your answer.
Answer
No, on a circle on going from one point around the circular path, the displacement is zero but the distance covered is equal to the circumference of the circle.

Question 4.
What type of motion is represented by a linear velocity-time graph? What does the slope of this line indicate?
Answer
The graph represents the motion with uniform acceleration, and the slope gives the acceleration of the moving body.

Question 5.
How will the equation of motion for an object moving with a uniform velocity changes?
Answer
Uniform velocity means acceleration is zero. So,
v=u +at ; a = 0 ⇒ v=u
When a = 0, s = ut, v² – u² = 2as
as a = 0 ⇒ v² = u² ⇒ n=u

Question 6.
A body moves in a circle of radius 2R. What is the distance covered and displacement of the body after 2 complete rounds?
Answer
Again, in this motion the initial and final positions are same
So, displacement t = final position – initial position = 0
Here, radius of circle = 2r So, circumference = 2n x 2r= 4πr
Now, since the body completes 2 rounds, so total distance travelled
= 2 x circumference = 2 x 47πr = 8πr .

Question 7.
An athlete runs along a circular track of radius 2R. What is his displacement after covering half a round? Answer
On completing, half around distance,
Displacement = 2 x half of circumference
= 2 x 1/2 x 2πr
= 2 x π x 20 [∵ r = 20 m] ⇒ 40 πm

Question 8.
A van accelerates uniformly and its velocity changes from 5m/s to 25 m/s in time t. Find its average velocity.
Answer
For a uniformly accelerated van, average velocity is given by
\(\cfrac { u+v }{ 2 } =\cfrac { 5+25 }{ 2 } =15m/s \)

Question 9.
Give S.I. unit of
(a) velocity
(b) retardation
Answer
(a) S.I. unit of velocity is m/s.
(b) S.I. unit of retardation is m/s² .

Question 10.
What remains constant in a uniform circular motion?
Answer
The speed of the body remains constant.

Question 11.
Which quantity is given by the area under velocity time-graph?
Answer
It gives the displacement of the object in the given time interval.

Question 12.
Why is uniform circular motion called accelerated motion?
Answer
Uniform circular motion is called accelerated motion because of its velocity changes at every point of motion due to change in its direction.

Question 13.
Can a body be at rest and in motion, at the same time?
Answer
Yes, a body can be at rest with respect to one reference point and at motion with respect to some other reference point.

Question 14.
There are three solids made up of aluminium, steel and wood of the same shape and same volume. Which of them would have the highest inertia and why?
Answer
The density of steel is more than that aluminium and wood. So, its mass is greater than the solids made of aluminium and wood. Inertia depends on the mass of the object. Hence, steel has a higher inertia.

Question 15.
What do you mean by momentum? Write its S.I. unit.
Answer
The momentum of a body is equal to the vector product of mass (m) and the velocity (v) of the body. In magnitude form, p = m x v and its S.I. the unit is kg m/s.

Question 16.
Which physical quantity corresponds to the rate of change of momentum?
Answer
A rate of change of momentum is directly proportional to force. So, it corresponds to the force.

Question 17.
A horse continuously to apply force in order to move a cart, with a constant velocity. Explain.
Answer
The cart will move with a constant velocity if and only if no external force acts on it. When the horse applies the force, the frictional force also acts between the wheels of the cart and road to oppose the motion. The cart will move with constant velocity, only if the force applied by the horse is equal to the frictional force.

Question 18.
What is a net force acting on a body moving with a constant velocity?
Answer
As there is no acceleration, the net force on it is zero.

Question 19.
Justify the statement “Mass of a body is the measure of its inertia”.
Answer
As we know that it is very difficult to change the state of rest or of uniform motion of a heavier body than that of a lighter one. So, mass is a measure of inertia.

Question 20.
A body is acted upon by two forces, but it does not move.
(a) What can you say about the two forces?
(b) What is the net force acting on the body?
Answer
(a) The two forces must be equal in magnitude and in opposite direction. So, they balance each other. As there is no unbalanced force, the body does not move.
(b) The net resultant force on the body is zero.

Question 21.
Under what condition a body moves with uniform velocity?
Answer
When forces acting on the body are balanced and no unbalanced force acts on it.

Question 22.
Why do action and reaction not cancel each other?
Answer
Action and reaction do not cancel each other, because they act on different bodies.

Question 23.
Name the principle on which a rocket works.
Answer
Law of conservation of momentum.

Question 24.
Calculate the mass of the body, when a force of 525 N produces an acceleration of 3.5 m/s².
Answer
We are given that Force (F) = 525 N
Acceleration (a) = 3.5 m/s².
Using, F = ma
\(\cfrac { F }{a} =\cfrac { 525 }{ 3.5 } =150m/s \)

Question 25.
State action and reaction in the case, when a bullet is fired from the gun.
Answer
Action – Force exerted on the bullet.
Reaction – Force exerted on the gun.

Question 26.
Why do we slip on a rainy day?
Answer
During rainy days, the wet ground becomes very smooth. The friction between our feet and the ground is reduced to the maximum. Thus, we slip.

Force and Motion Short Answer Type Questions

Question 1.
State Newton’s first law of motion and give its one example.
Answer
First Law of Motion:
Its states that a body at rest will remain at rest and a body in motion will continue in motion in a straight line with uniform speed unless it is compelled by some external force to change its state of rest or of uniform motion.
Example:
When a bus starts moving all of a sudden, the head of the passenger sitting in the bus strikes the back of his seat. This can be explained on the basis of the first law of motion. The lower part of the body of the passenger remains in contact with the body of the bus, but the upper part is free. When the bus takes a sudden start, the bus comes in motion and so the lower part of the body, but the head and upper part of the passenger’s body not in contact with the bus, tend to remain at rest and thus, jerked backwards. Similarly, we can explain the jerking of passengers in the forward direction of a bus, when the moving bus stops all of a sudden.

Question 2.
State Newton’s third law of motion and give its example.
Answer
Third law of motion: It states that to every action, there is an equal and opposite reaction. Action and reaction always operate on different bodies.
Example:
When a man jumps from a boat on to the bank of a river, then he pushes the boat behind with his leg (action) and the boat pushes (reaction) the man in the opposite direction. Because of this, the man move towards the bank of the river and the boat moves away from the bank in the opposite direction.

Question 3.
Why does a gun give a jerk to shoulder of the gunman, on firing a bullet from the gun?
Answer
When a bullet is fired from a gun, the force sending the bullet forward (action) is equal to the force sending the gun backward (reaction). But the mass of the gun is more than the mass of a bullet, so it moves only a little distance backwards and gives a backward jerk on the shoulder of the gunman.

Question 4.
Why does a man slip when his footfalls on a banana skin, lying on road?
Answer
A man walks easily on the road because there is friction between foot and the ground. A man slips when his footfalls on a banana skin lying on the road due to the absence of friction.

Question 5.
Why is it advised to tie luggage kept on the roof of a bus with a rope?
Ans.
Luggage on the top of the bus is not a compact part of the bus. When a moving bus takes a sharp turn or suddenly applies brakes to stop, the luggage placed loosely on the roof of the bus continues moving forward (inertia of motion) and is likely to fall off the bus. Conversely, if a stationary bus accelerates suddenly, the luggage tends to remain in the same state (inertia of rest) and hence slides backward
To avoid falling of luggage off the bus, it is advised to tie it with a rope.

Question 6.
State and explain Newton’s second law of motion. Derive the expression F = ma.
Answer
Newton’s second law of motion states that the force exerted by a body is directly proportional to the rate of change of its momentum. For a body of mass ‘m’, whose velocity changes from u to v in time t, when force ‘F’ is applied.

Question 7.
Why does a gun recoil when a bullet is fired? Calculate the velocity of recoil of the gun.
Or
When the bullet is fired from a gun, the gun gives a kick in the backward direction. Explain why?
Answer
When the bullet is fired from a gun the gun gives a kick in the backward direction. The reason behind is the force exerted on the bullet, known as a reaction. Since the mass of gun is large than the mass of a bullet, so the gun recoil with a velocity much lesser than the velocity with which the bullet moves forward.

Question 8.
A bullet shot with high velocity pierces through a window pane, whereas, the pane is shattered by a pebble thrown at it. Why?
Answer
A bullet moving with high velocity has a large momentum. When it strikes the window pane, the velocity decreases and momentum reduces to a very small value. This sudden change in momentum exerts a large impulsive force enough to pierce through the window pane, making a hole. On the other hand, the velocity of a pebble thrown at it is not very high, its momentum is less. So. change in momentum (or force) is less which only make cracks in the window pane.

Question 9.
(a) Define the buoyant force. Discuss the factors on which buoyant force depends.
(b) State Archimedes’ principle. Explain the law of floatation of bodies in a liquid.
Answer
(a) The upward force exerted by a liquid on the body, immersed in the liquid is known as the upthrust or buoyant force. Buoyant force acting on a body depends on the volume of the body submerged in the liquid and the density of the liquid in which the body is immersed.

(b) Archimedes determined the amount of buoyant force exerted by the liquid on the body. According to him, when a body is wholly or partially immersed in a liquid at rest, it experiences an upthrust, equal to the weight of the liquid displaced by the body.

• A body will sink in a liquid if its density is more than that of the liquid in which it is immersed.
• The body floats being completely immersed in water if the density of the body is equal to the density of the liquid.
• The body floats being partially immersed if the density of the body is less than the density of liquid

Question 10.
Give a reason for the following:
(a) The cork floats while the nail sinks when both are placed on the surface of the water.
(b) You feel lighter when you swim.
(c) It is easier to walk on soft sand with a flat shoe than a pencil – heeled shoe.
Answer
(a) The density of cork is less than that of water, whereas the density of a nail is greater than that of water. A substance whose density is less than a liquid will float on the surface of that liquid. Thus, a cork floats in water. On the other hand, a substance whose density is greater than that of a liquid will sink in that liquid. Thus, a nail sinks in water.
(b) We feel lighter when we swim, due to buoyancy upward force which is acting on our body by water
(c) The larger area of flat shoe exerts less pressure as compared to the pencil heeled shoe. Due to greater pressure, the sand under pencil-heeled shoe sinks in greater depth and therefore, it is difficult to walk with a pencil- heeled shoe on the sand. On the other hand, flat shoes exert less pressure and do not sink down in the sand.

Force and Motion Long Answer Type Questions

Question 1.
Explain uniform motion and non­uniform motion by the distance-time graph.
Answer
Uniform motion-If an object travels an equal distance in equal intervals of time, then the motion of the object is said to be uniform motion. For example, a car moves with a speed of 10 m/s is in uniform motion as explained below:
The distances covered by it are as follows-

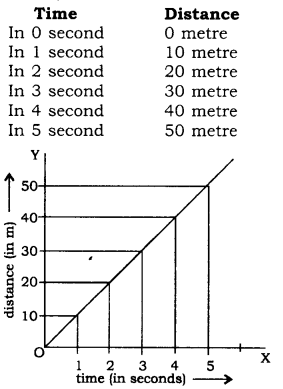
Draw two lines OX and OY at right angles.Take on OX, 1 cm = 1 second and on OY, 1 cm =10 metres. Show the above data on the graph. We get a straight line OP which represents uniform motion. Non-uniform Motion: If an object travels unequal distance in equal time intervals, then the motion of the object is said to be non-uniform motion.

For Example, A car is in motion with unequal speed, then the distances covered per second will be unequal. The distances travelled by car per second are as follows:

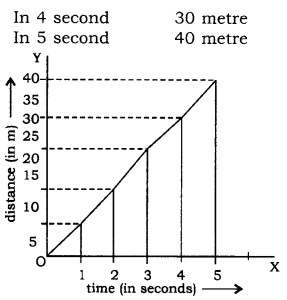
If a graph is drawn between distance and time, then we get a curved line graph. The graph shows a non-uniform motion. It is to be noted that non­uniform motion is called accelerated motion.

If the slope increases, then it shows increasing speed. If the slope decreases, then it shows decreasing speed.

Question 2.
State the law of action and reaction. Explain with a suitable and necessary diagram that

1. forces of action and reaction operate on two different objects.
2. forces of action and reaction are equal, but they act in opposite direction.

Answer
When a force acts on a body, then it is called the action. The force produced as a result of action acts on another object but in opposite direction is called reaction. Newton formulated a law in relation to action and reaction, which is called Newton’s third law of motion.According to this law, for every action, there is an equal and opposite reaction. Action and reaction always operate on different objects but in opposite directions.

(1) Action and reaction act on two different objects.
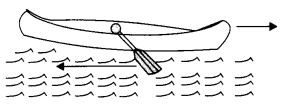
Experiment: Take an oil funnel and fill half of it with water and fix it on a small boat, as shown in the figure. The funnel is heated at the bottom with the help of a lamp. When steam begins to come out from the jet fastly, the boat experiences a force in a backward direction, and it begins to move in a direction opposite to the direction of the outgoing steam the body. It can also be stated as: The rate of change of momentum is equal to the force applied to the body and the change in momentum always takes place in the direction of the force. From this experiment, it is clear that the force (action) due to the outgoing steam acts in a forward direction and force of reactions acts, i.e., moving boats in the opposite direction. This proves that action and reaction act on two different objects.

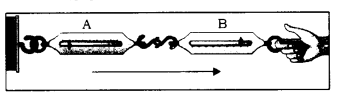
(2) Experiment: Take two similar spring balances, as shown in the figure. Fix one spring balance to a rigid support and then fix the hook of another spring balance in its hook, and stretch (pull) the whole system gently. Observe the readings of both the spring balances. We see that the reading of both the spring balances is exactly equal. If one balance reads 5 kg, the other also read 5 kg. Obviously, the tension of the first on the second spring balance is exactly equal the tension of the second on the first spring balance. This means that the action and reaction forces are equal and opposite.

Question 3.
State Newton’s second law of motion. Verify it by an experiment.
Answer
Newton’s second law of motion-The acceleration produced in the body by the action of a force acting on it is directly proportional to the force and inversely proportional to the mass of the body. It can also be started as: The rate of change of momentum is equal to the force applied to the body and the change in momentum always takes place in the direction of the force.

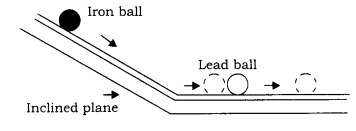
Verification: We take an inclined plank, which ends in a horizontal plank as shown in the figure. We place an iron ball at a height on the inclined plank and release it. It starts rolling down the inclined plank. After reaching the lower end of the inclined plank, it keeps on rolling on the horizontal plank and strikes the lead ball placed at some distance from the lower end of the inclined plank. Due to the collision, the lead ball moves some distance before coming to rest, we note down this distance.

Now, we take an aluminium ball in place of lead ball, whose diameter is equal to the diameter of the lead ball and place it at the point where the lead ball was earlier placed on the horizontal plank before being struck by the iron ball. It is also hit by the same iron ball, rolling down from the inclined plank from the same height as in the previous case. We note down the distance moved by the aluminium ball, after colliding with the iron ball. We find that distance moved by the aluminium ball is greater than the distance moved by the lead ball.

The iron ball on striking the lead and aluminium balls pushes them with the same force. Since the mass of aluminium ball is less than that of the lead ball, it means that when the same force acts on two bodies of different masses, lighter one will experience more acceleration than the heavier one. Hence, we conclude that in a body acceleration produced by a force is inversely proportional to the mass of the body, i.e.
\(a\propto \frac { F }{ m } \)……………..(i)

Now we take two balls, one of iron I  and other of aluminium of the same diameter and let them strike a glass marble placed at the same point on the horizontal plank separately. After rolling them from the same point of the inclined plank, we find that the iron ball imparts greater velocity to the marble then the aluminium ball, hence it means that iron ball applies greater force than aluminium ball. This leads us to the conclusion that acceleration is proportional to the force acting on it. Hence, a ∝ F … (ii)
Combining (i) and (ii), we get
or F ∝ ma or F = Kma .
We select the unit of force, in such a way that the value of K becomes one. Hence, F = ma.
This relation can also be obtained from Newton’s second law. Hence, Newton’s second law of motion is verified.

Force and Motion Additional Question Solved

Question 1.
A car initially moving with a speed of 10m/s is uniformly accelerated for 20 seconds. Value of acceleration is 4 m/s. What will be its velocity after 20 seconds and what distance it will cover in 20 sec?
Answer
From first equation of motion,
v = u + at
or v = 10 + 4 x 20
= 10 + 80 = 90m/s
Again from second equation of motion
s = ut +\(\frac { 1 }{ 2 } \) at²
⇒ s = 10 x 20 +\(\frac { 1 }{ 2 } \) x 4 x (20)²
⇒ 200 + \(\frac { 1 }{ 2 } \) x 4x 400
⇒ s = 200 + 800 = 1000 metres

Question 2.
A truck starts from rest and rolls down a hill with a constant acceleration. It travels a distance of 400 m in 20 s. Find its acceleration. Find the force acting on it, if its mass is 7 metric tonnes.
[Hint: 1 metric tonne = 1000 kg]
Answer
The initial velocity of the truck (u) = 0 (As the truck is initially at rest)
Distance covered (s) = 400 m,
Time (t) = 20 sec
Mass of the truck (m)
= 7 metric tonnes = 7 x 1000
=7000 kg
To find: Acceleration (a) = ?
Force (F) =?
Using second equation of motion
S = ut + \(\frac { 1 }{ 2 } \) at
400 = 0 x 20 + \(\frac { 1 }{ 2 } \) x a x (20)²
⇒ 400 = \(\frac { 1 }{ 2 } \) x a x 400
⇒ a = 2m/s² Now F = ma = 7000 x 2
= 14000 kgm / s² = 14000 Newton

Question 3.
A motor car is moving with a velocity of 108 km/ h and it takes 4 sec to stop after the brakes one applied. Calculate the force exerted by the brakes on the motor car if its mass along with the passengers is 1000 kg.
Answer
We are given that
Initial velocity of motor car = 108 km/h
⇒\((u)=\frac { 108\times 1000 }{ 60\times 60 } =30m/s \)
Final velocity (v) = 0 m/s
Total mass of the motor car along with its passengers (m) = 1000 kg.
Time is taken to stop the motor car (t) = 4 sec.

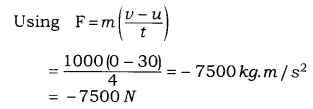
The negative sign shows that the force exerted by the brakes is opposite to the direction of motion of the motor car.

Question 4.
How much momentum will a dump bell of mass 10 kg transfer to the floor if it falls from the height of 80 cm? Take its downward acceleration to be 10 m/s².
Answer
We are given that
Mass of dump bell (m) = 10 kg
Initial velocity (u) = 0 Let final velocity be v.
Distance (s) = 80 cm= \(\frac { 80 }{ 100 } \) = 0.8m
Acceleration (a) = 10 m/s²
From third equation of motion,
v² = u² + 2 as
⇒ v² = 0 + 2 x 10 x 0.8
⇒ v² = 16
⇒ v = 4m/s
Momentum of dumb bell transformed to the ground = mv
= 10 x 4 = 40 kg m/s

Question 5.
A car starts from rest and moves along the x-axis with constant acceleration 5m/ s² for 8 sec. If it then continues with constant velocity, what distance will the car covers in 12 seconds start from the rest?
Answer
We are given that
Case – I:
when t = 0, u = 0 when t = 8 sec, v = ?
Acceleration (a) = 5 m/s²
∴ v = u + at
= 0 + 5 x 8 = 40 m/s
s = ut + \(\frac { 1 }{ 2 } \) at²
s = 0 + \(\frac { 1 }{ 2 } \) x 5 x (8)² = \(\frac { 1 }{ 2 } \) x 5 x 64 = 160m

Case-II: t = 8 sec to t = 12 sec.
Distance = speed x time
= 40 x 4 = 160 m.
So, the total distance travelled
= 160 + 160 = 320 m.

Question 6.
The velocity-time graph for an object is shown in the following figure:

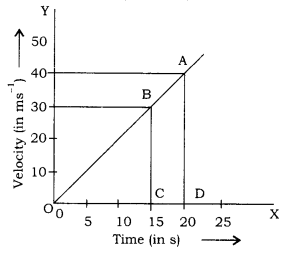
1. State the type of motion that the graph represents.
2. What does the slope of the graph represent?
3. What does the area under graph represent?
4. Calculate the distance travelled by the object in 15 s.

Answer
(1) Uniformly accelerated motion, since the slope of the velocity-time graph is positive and uniform.
(2) It represents acceleration.
(3) The area below the velocity-time graph and time axis represents the distance covered.
(4) The area covered in 15 s i.e., area of triangle OBC gives the distance covered in 15 s.
∴ Distance covered
= \(\frac { 1 }{ 2 } \) x BC x OC = \(\frac { 1 }{ 2 } \) x 30 x 15 Distance = 225 m.

Question 7.
A train is travelling at a speed of 90 km/h. Brakes are applied as to produce a uniform acceleration of -0.5 ms^-2. Find how far the train will go before it is brought to rest.
Answer
We are given that
Initial speed (u) = 90 kmh^-1
\(=\frac { 90\times 1000 }{ 60\times 60 } =25m{ s }^{ -1 } \)

Question 8.
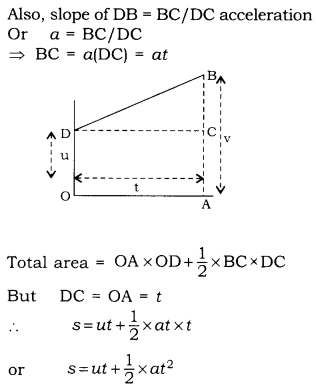
Derive graphically, the equation for velocity- time relation: for an object travelling distance ‘s’ in time t under uniform acceleration.
Answer
Diagrammatic representation of motion is shown below. Distance travelled is equal to the sum of the area of rectangle OACD and area of triangle BCD.

Question 9.
The velocity-time graph of a body is as shown in the graph:

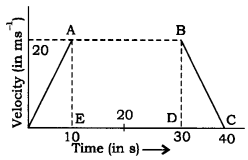
1. State the kind of motion represented by OA and AB.
2. What is the velocity of the body after 10s and after 30 s?
3. Calculate retardation of the body.
4. Calculate the distance covered by the body between 10th and 30th second.

Answer
(1) OA represents uniform acceleration since the slope of OA in the velocity-time graph is having a uniform positive slope. AB represents the uniform velocity of 20 ms^-1. Since the slope of AB is zero hence, acceleration is zero.
(2) After 10s, the velocity is 20 ms^-1 up to 30s and after 30 s, the velocity is uniformly restarted to zero after 40 s.
(3) Retardation is uniform and it is equal to the slope of BC, i.e.
\( Slope\quad of\quad BC=\frac { BD }{ DC } =\frac { 20 }{ 40-30 } =2m{ s }^{ -2 } \)
And acceleration = – 2 ms^-2
(4) Distance covered by the body between the 10th and 30th second
= 20 x 20 = 400 metres

Question 10.
A stone of 1 kg is thrown with a velocity of 20 ms^-2 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice?
Answer
Mass of stone (m) = 1kg;
Distance covered (s) = 50 m;
Initial velocity (u) = 20 ms^-1;
Final velocity (ν) = Zero;
Acceleration of the stone (a) =?
Force of friction (F) =?
Using the third equation, we have

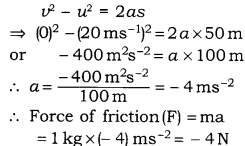
Minus sign shows that the force of friction acts in the opposite direction.

Question 11.
A bullet of mass lOg travel­ling horizontally with a velocity of 150 ms^-1 strikes a stationary wooden block and comes to rest in 0.03 s. Cal­culate the distance of penetration of the bullet into the block. Also, calculate the magnitude of the force exerted by the wooden block on the bullet.
Answer
Mass of bullet (m) = 10 g = 0.01 kg
Initial velocity of bullet (u) =150 ms
Final velocity of bullet (u) = 0 [As the bullet comes to rest]
Time (t) = 0.03 s ; Acceleration (a) = ?

(1) From the first equation of motion
v = u + at = 0 = 150 + a x 0.03
⇒ \(a=\frac { -150 }{ 0.03 } =-5000m{ s }^{ 2 } \)

(2) The distance of penetration of the bullet into the block
s = ut+ \(\cfrac { 1 }{ 2 } \) at²
= 150 x 0.03 + \(\frac { 1 }{ 2 } \) x (- 5000) x (0.03)²
= 4.5 – 2.25  = 2.25m

(3) The magnitude of the force exerted by the wooden block on the bullet
F = ma = 0.01 x 5000 = 50 N
⇒ F = 50 Newton

Question 12.
An object of mass 100 kg is accelerated uniformly from a velocity of 5 m/ s to 8 m/s in 6 s. Calculate the initial and final momentum of the object. Also, find the magnitude of the force exerted on the object.
Answer
We are given that
Mass of object (m) = 100 kg
Initial velocity (u) = 5 m/s
Final velocity (ν) = 8 m/s
Time = 6 sec.
Initial momentum of the object
= mu = 100 x 5 = 500 kg m/s
∴ Final momentum of the object
= mv – 100 x 8 = 800 kg m/s
∴ Magnitude of the force exerted on the object
\((F)=\cfrac { Change\quad in\quad momentum }{ Time } \)
\(=\cfrac { 800-500 }{ 6 } \cfrac { 300 }{ 6 } =50\quad Newton \)

Question 13.
An object of mass 1 kg travelling in a straight line with a velocity of 10 ms~’ collides with and sticks to a stationary wooden block of mass 5 kg. Then they both move off together in the same straight line. Calculate the velocity of the combined object.
Answer
(1) We are given that
Mass of object (m₁)= 1 kg
Velocity of object before collision (U₁) = 10 m/s
Mass of wooden block (m₂) = 5 kg
Velocity of object after collision (u₂) = 0 m/s
.’. Total momentum before the impact =m₁u₁+ m₂u₂
= 1 x 10 + 5 x 0 = 10 kg m/s
According to the law of conservation of momentum (When no external force act on the system)
Total momentum after the impact = 10 kg m/s

(2) Mass of the combined object,
M = Mass of object + mass of block = 1 + 5 = 6 kg
Let V be the velocity of the combined object after the impact.
Movement of combined objects
= Total momentum after the impact
i.e. 6 V = 10
V = 10/6= 1.67 m/s

Question 14.
An object starting from rest travels 20m in the first 2 sec. and 160 m in the next 4 sec. What will be velocity after 7 sec from the start?
Answer

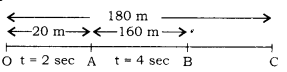
Motion from O to A; u = 0, t = 2 sec, s = 20 m
Acceleration (a) = ?
s = ut+ \(\frac { 1 }{ 2 } \) at²
(Using the 2nd equation of motion)
⇒20 = 0 + \(\frac { 1 }{ 2 } \) x a x (2)²
⇒2a = 20 ⇒ a = 10m/s²
Motion from O to B
u = 0, S = (20 + 160) = 180 m,
t = 2 + 4 = 6 sec, a = ?
Again,
s = ut +\(\frac { 1 }{ 2 } \) at²
180 = 0 +\(\frac { 1 }{ 2 } \) x a x (6)²
180 = 18a ⇒a = 10m/s²
This shows that body is moving with constant acceleration.
Motion from O to C,
u = 0, t = 7 sec, a = 10 m/s² v = ?
v = u + at ⇒ y = 0 + 10 x 7⇒ v = 70 m/s

Question 15.
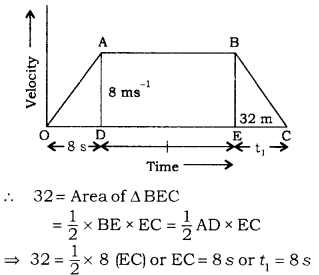
A motor car starting from rest moves with uniform acceleration and attains a velocity of 8 ms ‘ in 8 s. It then moves with uniform velocity and is finally brought to rest in 32 m under uniform retardation. The total distance covered by the car is 464 m. Find the value of acceleration, retardation and the total time is taken.
Answer
The figure shows the velocity-time graph. OA shows uniform acceleration; BC, uniform retardation and AB, the uniform velocity.
Now the area of velocity-time graph is equal to the distance covered.

Question 16.
Define pressure. A pressure of 100 Pa acts on a surface of area 15 cm² by a block of mass ‘m’. Calculate
Answer
The effect of thrust per unit area is called pressure.
Pressure = 100 Pa

Question 17.
An object of mass 500 g is immersed into measuring jar containing water. The initial level of water in the measuring jar is 50cc. Due to the immersion of the object the water rises in the measuring jar and reaches to 100cc. Calculate the mass of the water displaced due to the imm.ersion of the object.
Answer
Water displaced
= 100cc – 50cc
= 50cc 1l= 1000cc
\(50cc=\cfrac { 50 }{ 1000 } l=\cfrac { 1 }{ 20 } l \)
Mass of the water displaced = \(\cfrac { 1 }{ 20 }kg \)

Question 18.
Which will exert more pressure: a 100 kg mass on the area of 100 cm² or a 50 kg mass on 25 cm²?
Answer

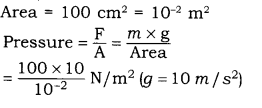
We hope the given RBSE Solutions for Class 9 Science Chapter 9 Force and Motion will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Science Chapter 9 Force and Motion, drop a comment below and we will get back to you at the earliest.