RBSE Class 10 Maths Board Paper 2018 are part of RBSE Class 10 Maths Board Model Papers. Here we have given Rajasthan RBSE Class 10 Maths Board Paper 2018.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Paper Set | Board Paper 2018 |
| Category | RBSE Model Papers |
Rajasthan RBSE Class 10 Maths Board Paper 2018
समय: 3 1/4 घण्टे
पूर्णांक: 80
परीक्षार्थियों के लिए सामान्य निर्देश :
- परीक्षार्थी सर्वप्रथम अपने प्रश्न-पत्र पर नामांक अनिवार्यतः लिखें
- सभी प्रश्न करने अनिवार्य हैं
- प्रत्येक प्रश्न का उत्तर दी गई उत्तर पुस्तिका में ही लिखे
- जिन प्रश्नों में आन्तरिक खण्ड हैं, उन सभी के उत्तर एक साथ ही लिखें
- प्रश्न-पत्र के हिन्दी व अंग्रेजी रुपान्तर में किसी प्रकार की त्रुटि/अन्तर/विरोधाभास होने पर हिन्दी भाषा के प्रश्न की सही मार्गे।
-
भाग प्रश्न संख्या अंक प्रत्येक प्रश्न अ 1-10 1 ब 11-15 2 स 16-25 3 द 26-30 6 - प्रश्न क्रमांक 27 और 29 में आन्तरिक विकल्प हैं
- अपनी उत्तर-पुस्तिका के पृष्ठों के दोनों और लिखिए। यदि कोई रफ कार्य करना हो, तो उत्तर-पुस्तिका के अंतिम पृष्ठों पर करें और इन्हें तिरछी लाइनों से काटकर उन पर ‘रफ कार्य’ लिख दें
- प्रश्न क्रमांक 26 का लेखाचित्र ग्राफ पेपर पर बनाइए।
भाग – अ
प्रश्न 1.
सूत्र एकाधिकेन पूर्वेण का प्रयोग करते हुए \(31 \frac { 1 } { 6 } \times 31 \frac { 5 } { 6 }\) का मान ज्ञात कीजिए।
प्रश्न 2.
हल कीजिए \(\frac { 1 } { x – 3 } + \frac { 1 } { x – 7 } = \frac { 1 } { x – 1 } + \frac { 1 } { x – 9 }\)
प्रश्न 3.
196 के अभाज्य गुणनखण्डों की घातों का योगफल लिखिए।
![]()
प्रश्न 4.
cos 50°. cosec 40° का मान लिखिए
प्रश्न 5.
यदि एक ऊर्ध्वाधर छड़ की लम्बाई तथा इसकी छाया की लम्बाई का अनुपात \(1 : \sqrt { 3 }\) हो, तो सूर्य का उन्नयन कोण ज्ञात कीजिए।
प्रश्न 6.
दो दिये गये बिन्दुओं से सम दूरस्थ बिन्दुओं का बिन्दुपथ लिखिए
प्रश्न 7.
वृत्त में केन्द्र से समान दूरी पर स्थित जीवाओं का अनुपात लिखिए
प्रश्न 8.
एक पासे के एक बार फेंकने पर विषम अंक आने की प्रायिकता ज्ञात कीजिए।
प्रश्न 9.
किसी नगर में टैक्सी का किराया पहले किलोमीटर का ₹ 5 और उसके बाद में ₹ 3 है यदि तय की गई दूरी x किमी और किराया ₹ y हो, तो इसे समीकरण रूप में व्यक्त कीजिए।
प्रश्न 10.
यदि एक खम्भे के आधार से 20 मीटर दूर स्थित प्लेटफार्म के एक बिन्दु से खम्भे की चोटी पर लगे हुए कैमरे का उन्नयन कोण 60° है तो खम्भे की ऊँचाई ज्ञात कीजिए
![]()
भाग – ब
प्रश्न 11.
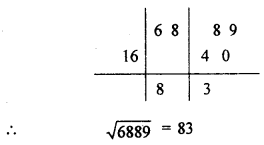
द्वन्द्व योग विधि से 6889 का वर्गमूल ज्ञात कीजिए।
प्रश्न 12.
यदि दो संख्याओं का गुणनफल 525 है और उनका महत्तम समापवर्तक 5 है, तो उनका लघुत्तम समापवयं ज्ञात कीजिए।
प्रश्न 13.
एक घन का सम्पूर्ण पृष्ठीय क्षेत्रफल 216 वर्ग मीटर है। घन की भुजा ज्ञात कीजिए।
प्रश्न 14.
एक अर्द्धगोले की त्रिज्या 7 सेमी. है, इसका सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
प्रश्न 15.
एक 24 मीटर ऊँचे पोल पर यातायात नियंत्रण के लिए CCTV कैमरा लगाया है ताकि यह पोल के शीर्ष से 25 मीटर दूर दृष्टि रेखा के आगे भी यातायात देख सकता है। पोल के चारों ओर अदर्शनीय वृत्त का क्षेत्रफल ज्ञात कीजिए।
भाग – स
प्रश्न 16.
विभाजन एल्गोरिथम पद्धति द्वारा बहुपद P(x) = x4 -3x2 + 4x – 3 को g(x) = x2 + 1 – 1 से भाग देने पर भागफल एवं शेषफल ज्ञात कीजिए।
![]()
प्रश्न 17.
यदि किसी समान्तर ओड़ी का दूसरा व तीसरा पद क्रमशः 3 और 5 हैं, तो इसके प्रथम 20 पदों को योगफल ज्ञात कीजिए।
प्रश्न 18.
एक मीनार के आधार से १ मीटर तथा 25 मीटर दूरी पर एक ही रेखा पर स्थित दो बिन्दुओं से देखने पर मीनार के शिखर के उनयन कोण परस्पर पूरक हैं। मीनार की ऊँचाई ज्ञात कीजिए।
प्रश्न 19.
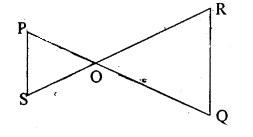
दी गई आकृति में यदि OP.OQ = OR.OS तो दर्शाइए ∠OPS = ∠ORQ व ∠OQR = ∠OSP.
प्रश्न 20.
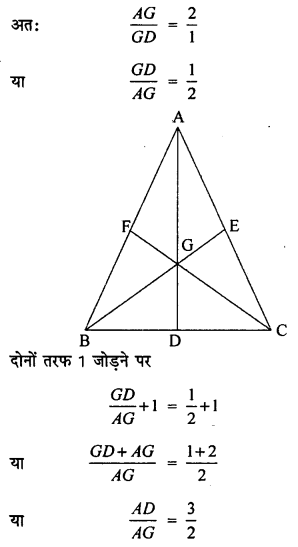
एक त्रिभुज ABC में माध्यिकाएँ AD, BE और CF एक बिन्दु से गुजरती हैं। यदि AD = 9 सेमी, GE = 4.2 सेमी. और | GC = 6 सेमी, तो AG, BE और FG की लम्बाइयों के मान ज्ञात कीजिए।
प्रश्न 21.
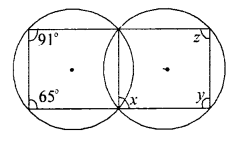
दी गई आकृति में कुछ कोणों को x, y और z से चिह्नित किया गया है इन कोणों के मान ज्ञात कीजिए
प्रश्न 22.
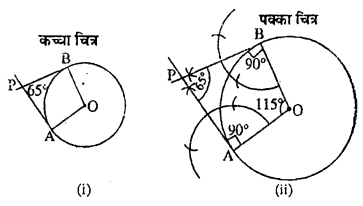
एक 4 सेमीत्रिज्या के वृत्त पर बाह्य बिन्दु P से दो स्पर्श रेखाओं PA तथा PB की रचना कीजिए। जहाँ PA तथा PB के मध्य कौण 65° है।
![]()
प्रश्न 23.
एक वृत्ताकार पार्क की त्रिज्या 4.2 मीटर है। पार्क के चारों ओर 1.4 मीटर चौड़ा रास्ता बना हुआ है। रास्ते का क्षेत्रफल ज्ञात कीजिए।
प्रश्न 24.
एक रोलर की लम्बाई 2.5 मीटर और व्यास 1.4 मीटर है। 10 चक्कर लगाने में रोलर कितना क्षेत्र समतल करेगा ?
प्रश्न 25.
एक थैले में एक सफेद गेंद, दो काली गेंद और तीन लाल गेंद एक ही आकार की हैं। इस थैले में से एक गेंद यादृच्छ या निकाली जाती है। प्रायिकता ज्ञात कीजिए।
- गेंद सफेद हो
- गेंद काली न हो
- गेंद लाल हो
भाग – द
प्रश्न 26.
निम्न रैखिक समीकरण युग्म को आलेखीय विधि द्वारा हुल कीजिए :
2x + y = 6, 2x -y = 2
अतः इसकी सहायता से सम्बन्ध 6x + 7y =p में p का मान ज्ञात कीजिए।
प्रश्न 27.
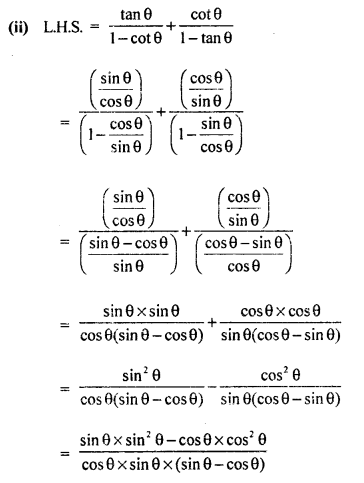
सिद्ध कीजिए :
(i) \(\sqrt { \frac { 1 + \cos \theta } { 1 – \cos \theta } } = \csc \theta + \cot \theta\)
(ii) \(\begin{array} { l } { \sqrt { 1 – \cos \theta } } \\ { \frac { \tan \theta } { 1 – \cot \theta } + \frac { \cot \theta } { 1 – \tan \theta } = 1 + \tan \theta + \cot \theta } \end{array}\)
अथवा
(i) यदि sinθ + cosθ = p और secθ + cosecθ = q हो तो सिद्धि कीजिए कि q(p2 – 1) = 2p
(ii) सिद्धि कीजिए:
\(\frac { \cos A } { 1 – \tan A } + \frac { \sin A } { 1 – \cot A } = \sin A + \cos A\)
![]()
प्रश्न 28.
(i) यदि बिन्दु (x, 3) और (5, 7) के बीच की दूरी 5 हो, तो x का मान ज्ञात कीजिए।
(ii) ज्ञात कीजिए रेखा 3x + y = 9 बिन्दुओं (1, 3) और ( 2, 7) को मिलाने वाले रेखा खण्ड को किस अनुपात में विभाजित करती है।
प्रश्न 29.
ABC एक समकोण त्रिभुज है जिसका ∠B समकोण है। भुजा AB पर D तथा भुजा BC पर बिन्दु E स्थित हैं। सिद्ध कीजिए। AE2 +CD2 = AC2 + DE2
अथवा
यदि एक चक्रीय चतुर्भुज की दो भुजाएँ समान्तर हों, तो सिद्ध कीजिए कि शेष भुजाएँ बराबर होंगी और विकर्ण भी बराबर होंगे।
प्रश्न 30.
निम्न बारंबारता बंटन के माध्यं बहुलक ज्ञात कीजिए:
| प्राप्तांक: | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| छात्रों की संख्या: | 4 | 28 | 42 | 20 | 6 |
हल
हल 1:
\(31 \times ( 31 + 1 ) / \frac { 1 } { 6 } \times \frac { 5 } { 6 }\)
\(= 31 \times 32 / \frac { 1 } { 6 } \times \frac { 5 } { 6 }\)
\(= 992 / \frac { 5 } { 36 }\)
\(= 992 \frac { 5 } { 36 }\)
संकेत:
- भिन्न योग \(\frac { 1 } { 6 } + \frac { 5 } { 6 } = 1\)
- शेष निखिलम् अंक समान = 31.
हल 2:
वाम पक्ष के हरों का योग = x – 3 + 1 -7 = 2x – 10
दक्षिण पक्ष के हरों का योग = x – 1 + x – 9 = 2x – 10
सूत्रानुसार
⇒ 2x – 10 = 0
⇒ 2x = 10
\(\Rightarrow \quad x = \frac { 10 } { 2 } = 5\)
![]()
हल 3:
196 के अभाज्य गुणनखण्ड
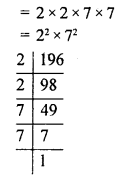
अतः 195 के अभाज्य गुणनखण्डों की घातों का योग = 2 + 2 = 4
हल 4:
⇒ cos (90° – 40°) . cosec 40°
⇒ sin 40° . cosec 40° [∵ cos (90° – θ) = sinθ]
⇒ 1 [∵sinθ × cosec θ = 1]
हल 5:
माना छड़ की लम्बाई = x इकाई है।
तब इसकी छाया = \(\sqrt { 3 } x\) इकाई होगी
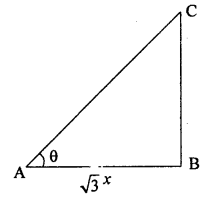
\(\tan \theta = \frac { B C } { A B }\)
\(\tan \theta = \frac { x } { \sqrt { 3 } x } = \frac { 1 } { \sqrt { 3 } }\)
tan θ = tan 30°
θ = 30°
अतः सूर्य का उन्नयन कोण 30 होगा
हल 6:
दिये हुए दो बिन्दुओं से समदूरस्थ किसी बिन्दु का बिन्दुपथ उन्हें मिलाने वाले रेखाखण्ड का लम्ब समद्विभाजक होता है
हल 7:
हम जानते हैं कि “किसी वृत्त की जीवायें केन्द्र से बराबर दूरी पर हों तो वे परस्पर बराबर होती हैं।”
अत: जौवाओं का अनुपात 1: 1 होगा
![]()
हल 8:
S={1, 2, 3, 4, 5, 6}
n(S) = 6
विषम अंक आना घटना (E)= {1, 3, 5}
n(E) = 3
\(\therefore \quad \mathrm { P } ( \mathrm { E } ) = \frac { n ( E ) } { n ( S ) } = \frac { 3 } { 6 } = \frac { 1 } { 2 }\)
हल 9:
पहले किलोमीटर का किराया = ₹ 5
अगले किलोमीटर का किराया = ₹ 3
तय की गई दूरी = x किमी.
और कुल किराया = ₹y
प्रश्नानुसार
y = 5 × 1 +3 (x – 1)
y = 5 + 3x – 3
y = 3x + 2
∴ 3x – y + 2 = 0
हल 10:
माना BC एक खम्भा है जिसकी ऊँचाई / मीटर (माना) है। खाने के आधार से 20 मीटर दूर स्थित प्लेटफार्म पर A एक बिन्दु है
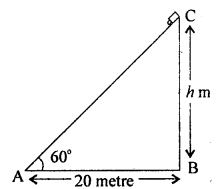
\(\therefore \quad \tan 60 ^ { \circ } = \frac { B C } { A B }\)
\(\Rightarrow \quad \quad \quad \sqrt { 3 } = \frac { h } { 20 }\)
\(\therefore \quad h = 20 \sqrt { 3 } = 20 \times 1.732\)
= 34.64 मीटर
अत: खम्भे की ऊँचाई = 34.64 मीटर
हल 11:
हल 12:
दिया हैदो संख्याओं का गुणनफल = 525
उनका महत्तम समापवर्तक = 5
हम जानते हैं
LCM × HCF = दो संख्याओं का गुणनफल

![]()
हल 13:
घन का सम्पूर्ण पृष्ठीय क्षेत्रफल = 216 वर्ग मीटर
घन की भुजा = ?
घने को सम्पूर्ण पृष्ठीय क्षेत्रफल = 6 × (भुजा)2
⇒ 216 – 6 × (भुजा)2
या (भुजा)2 \(= \frac { 216 } { 6 } = 36\)
∴ भुजा \(= \sqrt { 36 } = 6\) मीटर
अत: घन की भुजा = 6 मीटर
हल 14:
दिया है r = 7 सेमी.
अर्द्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल = 3πr2
मान रखने पर \(= 3 \times \frac { 22 } { 7 } \times 7 \times 7 = 462\) वर्ग सेमी.
हल 15:
पाइथागोरस प्रमेय से
AC2 = AB2 + BC2
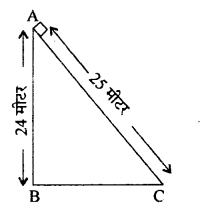
⇒ BC2 = AC2 – AB2
\(\Rightarrow \quad \mathrm { BC } = \sqrt { A C ^ { 2 } – A B ^ { 2 } }\)
\(= \sqrt { ( 25 ) ^ { 2 } – ( 24 ) ^ { 2 } }\)
\(= \sqrt { 625 – 576 } = \sqrt { 49 }\)
⇒ BC = 7 मीटर
अत: पोल के पाद से 7 मीटर की दूरी के आगे का यातायात | दिखाई देगा। पोल के चारों ओर अदर्शनीय वृत्त का क्षेत्रफल
= πr2
\(= \frac { 22 } { 7 } \times 7 \times 7 = 154\) वर्ग मीटर
हल 16:
सर्वप्रथम हम बहुपद को मानक रूप में लिखते हैं तब विभाजन प्रक्रिया करते हैं।
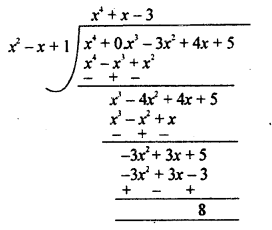
अतः भागफल x2 + x – 3, शेषफल = 8
यहाँ, भाजक × भागफल + शेषफल
= ( x 2 – x + 1) × (x2 + x – 3) + 8
= x4 – x3 – 3x2 – x3 – x2 + 3x + x2 + x – 3 + 8
= x4 – 3x2 + 4x + 5
= भाज्य
अतः विभाजन ऐल्गोरिथ्म सत्यापित होती है।
![]()
हल 17:
समान्तर श्रेढी का व पद
an = a+ (n – 1) d
∴ a2= a + d
a3 = a + 2d
अतः प्रश्नानुसार 3 = a + d ……………… (1)
5 = a + 2d …………….. (2)
समीकरण (2) में से समीकरण (1) को घटाने पर
5 -3 = a + 2d – a – d
⇒ 2= d
d का मान समीकरण (1) में रखने पर
3 = a + 2
a = 3 – 2 = 1
हम जानते हैं \(S _ { n } = \frac { n } { 2 } ( 2 a + ( n – 1 ) d )\)
\(= \frac { 20 } { 2 } ( 2 \times 1 + ( 20 – 1 ) \times 2 )\)
= 10 (2 + 19 × 2)
= 10 (2 + 38)= 10 × 40 = 400
हल 18:
माना मीनार की ऊँचाई AB = h मीटर
तथा C व D बिन्दु इस प्रकार हैं कि BC = 9 मीटर, BD = 25 मीटर
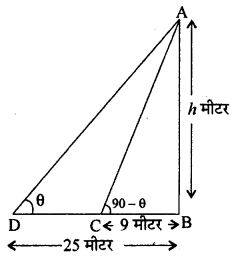
यदि ∠ADB = 0
तो ∠ACB = 90° – θ
समकोण ∆ABD में

हल 19:
∆POS व ∆QOR में OP.OQ = OR.OS दिया हुआ है
अतः \(\frac { \mathrm { OP } } { \mathrm { OS } } = \frac { \mathrm { OR } } { \mathrm { OQ } }\) …………..(1)
तथा ∠POS = ∠ROQ (शीर्षाभिमुख कोण) ……….(2)
समीकरण (1) व (2) से
∆POS ~ ∆ROQ
∴ इसलिए ∠P = ∠R एवं ∠S = ∠Q (समरूप त्रिभुजों के संगत कोण)
अत: ∠OPS – ∠ORQ व ∠OQR = ∠OSP इतिसिद्धम्
![]()
हल 20:
हम जानते हैं कि केन्द्रक G त्रिभुज की माध्यिका को 2 : 1 के अनुपात में विभाजित करता है

हल 21:
दिये गये चित्र में ∆BEF एक चक्रीय चतुर्भुज के बहिष्कोण उनके अन्तराभिमुख कोण के बराबर होते हैं। इस कारण से
∠BAF = ∠BED = 65°
चित्र से ∠E + ∠C = 180°
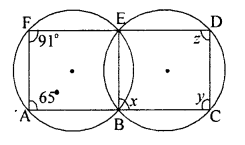
∵ BEDC एक चक्रीय चतुर्भुज हैं जिसमें आमने-सामने के कोणों का योग 180° होता है।
⇒ 65° + y = 180°
∴ y = 180° – 65° = 115°
इसी प्रकार ∠AFE = ∠CBE
⇒ 91° = x
∴ x + 91°
हम जानते हैं
x + z = 180°
z = 180° – x
z = 180° – 91° = 89°
![]()
हल 22:
चूँकि ∠APB = 65° दिया हुआ
∠A =∠B = 90°
अतः चतुर्भुज AOBP का चौथा कोण
∠AOB = 360° -(65° + 90° + 90°)
= 36 -245°=115°
अर्थात् जीवा OA व OB के मध्य
∠AOB =115°
रचना
(i) 4 सेमी. क्रिया का वृत्त बनाया एवं क्रियाएँ OA व OB के मध्य 115° का कोण बनाया।
(ii) OA व OB के A व B पर लम्ब क्रमश: AP व BP खींचे जो एक-दूसरे को P पर मिलते हैं। ∠APB को मापने पर ∠APB = 65° प्राप्त होता है। इस प्रकार अभीष्ट्र स्पर्श रेखाओं की रचना होती है।
हल 23:
दिया है
R1 = 4.2 मीटर
R2 = 4.2 + 1.4 = 5.6 मीटर
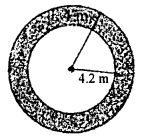
रास्ते का क्षेत्रफल = πR22 – πR12
= π(R22 – R12)
= π(R2 – R1) (R2 + R1)
मान रखने पर = π(5.6 – 4.2)(5.6 + 4.2)
= 1.4 × 9.8
\(= \frac { 22 } { 7 } \times 1.4 \times 9.8\)
= 22 × 0.2 × 9.8
= 43.12 वर्ग मीटर
![]()
हल 24:
दिया गया है
रोलर की लम्बाई = 2.5 मीटर,
अर्थात् रोलर की ऊँचाई = 2.5 मीटर
रोलर का व्यास = 14 मीटर
h = 2.5 मीटर
रोलर का एक चक्कर में क्षेत्रफल = रोलर का वक़ पृष्ठीय क्षेत्रफल
= 2πrh
= π × (2r) × h
\(= \frac { 22 } { 7 } \times 1.4 \times 2.5\)
= 22 × 0.2 × 25
= 11 वर्ग मीटर
अतः 10 चक्कर लगाने में क्षेत्रफल = 11 × 10
= 110 वर्ग मीटर
हल 25:
थैले में गेंदों की कुल संख्या
= 1 सफेद + 2 काली + 3 लाल
= 6
थैले में से एक गेंद यादृच्छया निकालने पर कुल सम्भावित परिणाम = 6
- गेंद सफेद होने की घटना के अनुकूल परिणाम = 1
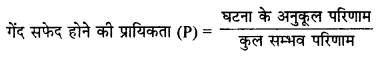
\(= \frac { 1 } { 6 }\) - गेंद काली होने की घटना के अनकूल परिणाम = 2

\(= \frac { 2 } { 6 } = \frac { 1 } { 3 }\)
अतः गेंद काली होने की प्रायिकता \(( P ) = \frac { 1 } { 3 }\)
तब गेंद काली न होने की प्रायिकता = 1 – गेंद काली होने की प्रायिकता
\(= 1 – \frac { 1 } { 3 } = \frac { 2 } { 3 }\) - गेंद लाल होने की घटना के अनुकूल परिणाम = 3

\(= \frac { 3 } { 6 } = \frac { 1 } { 2 }\)
![]()
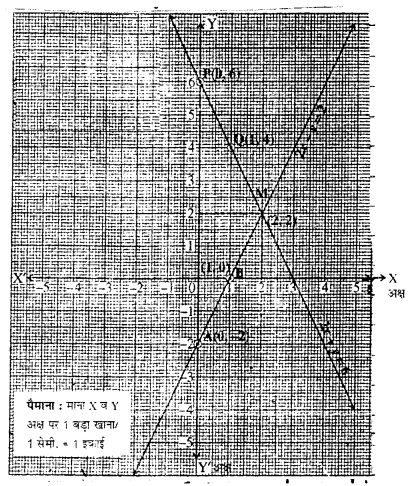
हल 26:
दिये गये रैखिक समीकरण युग्म
2x + y = 6 ………………. (1)
2x – y = 2 ………………… (2)
समीकरण (1) के संगत बिन्दु सारणी प्राप्त करने पर
x = 0 पर 2 × 0 + y = 6
0 + y = 6
या y = 6
तथा x = 1 पर 2 × 1 + y = 6
⇒ 2 + y = 6
या y = 6 – 2 = 4
इस प्रकार समीकरण (1) की विन्दु सारणी निम्न प्रकार प्राप्त होगी
| x | 0 | 1 |
| y | 6 | 5 |
अत: समीकरण (2) के संगत बिन्दु सारणी प्राप्त करते हैं। समीकरण (2) में x = 0 रखने पर
2x – y = 2
2 × 0 – y = 2
0 – y = 2
∴ y = -2
तथा y = 0 रखने पर ।
2x -0 = 2
⇒ 2x = 2
अत: समीकरण (2) की विन्दु सारणी निम्न प्रकार प्राप्त होती है
| x | 0 | 1 |
| y | -2 | 0 |
उपरोक्त समीकरण (1) एवं (2) से प्राप्त बिन्दु सारणियों की सहायता से ग्राफ पेपर पर रेखायुग्म का निरूपण करते हैं।
दोनों रेखायें विन्दु M (2, 2) पर प्रतिच्छेद करती हैं। अत: समीकरण निकाय का अभीष्ट हुल x = 2 व y = 2 हैं।
x = 2 व y = 2 को दिये गये सम्बन्ध 6x – 7y = P में रखने पर
6 × 2 + 7 × 2 = P
⇒ 12 + 14 = P
P = 26
![]()
हल 27:

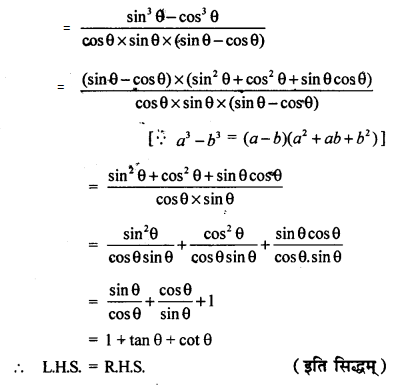

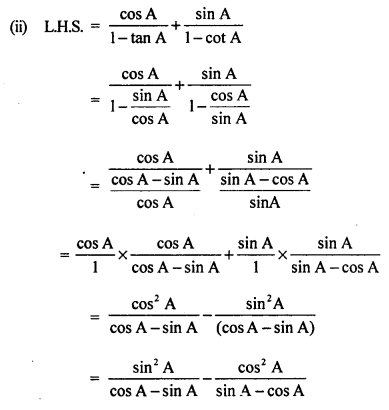
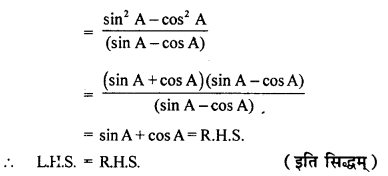
![]()
हल 28:
(i) दो बिन्दुओं के बीच की दूरी
\(d = \sqrt { \left( x _ { 2 } – x _ { 1 } \right) ^ { 2 } + \left( y _ { 2 } – y _ { 1 } \right) ^ { 2 } }\)
\(5 = \sqrt { ( 5 – x ) ^ { 2 } + ( 7 – 3 ) ^ { 2 } }\)
दोनों तरफ वर्ग करने पर
25 = (5 – x)2
⇒ 25 – 16 = (5 – x)2
⇒ 25 – 16 = (5 – 3)
या (5 – x)2 = 9
\(\therefore ( 5 – x ) = \pm \sqrt { 9 } = \pm 3\)
स्थिति I धनात्मक चिह्न लेने पर
5 – x = 3
∴ x = 5 + 3 = 8
स्थिति II ऋणात्मक चिह्न लेने पर
5 – x = -3
∴ 5 + 3 = 8
अतः = 2, 8
(ii) माना बिन्दु A(1, 3) तथा B (2, 7) को मिलाने वाला रेखाखण्ड 3x + y = 9 को λ = 1 में विभाजित करता है अत: विभाजन बिन्दु के निर्देशांक:
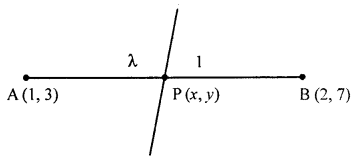
\(x = \frac { m _ { 1 } x _ { 2 } + m _ { 2 } x _ { 1 } } { m _ { 1 } + m _ { 2 } }\)
तथा \(y = \frac { m _ { 1 } y _ { 2 } + m _ { 2 } y _ { 1 } } { m _ { 1 } + m _ { 2 } }\)
\(\therefore \quad x = \frac { \lambda ( 2 ) + 1 ( 1 ) } { \lambda + 1 } = \frac { 2 \lambda + 1 } { \lambda + 1 }\)
इसी प्रकार
\(y = \frac { \lambda ( 7 ) + 1 ( 3 ) } { \lambda + 1 } = \frac { 7 \lambda + 3 } { \lambda + 1 }\)
अत: विभाजन बिन्दु
\(= P \left( \frac { 2 \lambda + l } { \lambda + 1 } , \frac { 7 \lambda + 3 } { \lambda + 1 } \right)\)
यह विन्दु रेखा 3x + y = 9 पर स्थित होंगे और इसको संतुष्ट करेंगे। अत: मान रखने पर
\(\Rightarrow 3 \left( \frac { 2 \lambda + 1 } { \lambda + 1 } \right) + \left( \frac { 7 \lambda + 3 } { \lambda + 1 } \right) = 9\)
\(\Rightarrow \frac { 6 \lambda + 3 } { \lambda + 1 } + \frac { 7 \lambda + 3 } { \lambda + 1 } = 9\)
⇒ 6λ + 3 + 7λ + 3 = 9 (λ + 1)
⇒ 13λ + 6 = 9λ + 9
⇒ 13λ – 9λ = 9 – 6
⇒ 4λ = 3
\(\therefore \lambda = \frac { 3 } { 4 }\)
अतः अभीष्ट अनुपात = 3 : 4 है।
![]()
हल 29:
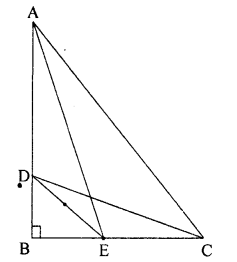
∆AABE समकोण त्रिभुज है तथा ∠B = 90°
∴ AE2 = AB 2 + BE2 ………………………. (1)
पुनः ∆DBC समकोण त्रिभुज हैं और ∠B = 90°
CD2 = BD2 + BC2 ……………………… (2)
(1) व (2) को जोड़ने पर AE2 + CD2 = (AB2 + BC2) + (BE2 + BD2) …………… (3)
इसी प्रकार समकोण ∆ABC एवं समकोण ∆DBE में
AC2 = AB2 + BC2 एवं DE2 = BE2 + BD2 ……….. (4)
(3) व (4) से
AE2 + CD2 = AC2 + DE2 इतिसिद्धम्
अथवा
हल-दिया है- चक्रीय चतुर्भुज ABCD में, AB || CD है।
सिद्ध करना है
(i) AD = BC
(ii) AC = BD
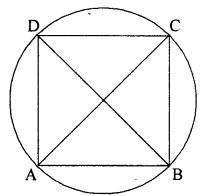
उपपत्ति:
∴ AB || DC और BC एक तिर्यक रेखा है,
अतः ∠ABC + ∠DCB = 180° ………………….. (1)
परन्तु ABCD एक चक्रीय चतुर्भुज हैं,
अतः ∠ABC + ∠ADC = 180° ………………. (2)
समीकरण (1) और (2) से
∠ABC + ∠DCB = ∠ABC + ∠ADC
या ∠DCB = ∠ADC …………….. (3)
अब ∆ADC और ∆BCD में,
∠ADC = ∠DCB (समीकरण (3) से)
∠DAC = ∠DBC (एक ही वृत्त खण्ड के कोण)
और . DC = DC (उभयनिष्ठ)
∴ ∆ADC ≅ ∆BCD (ASA से)
अतः सर्वांगसम त्रिभुजों की संगत भुजाएँ समान होंगी,
अर्थात् AD = BC
और AC = BD इति सिद्धम्
![]()
हल 30:
| प्राप्तांक | छाओं की संख्या (f) | मध्यमान (x) | f.x. |
| 20-30 | 4 | 28 | 100 |
| 30-40 | 28 | 35 | 980 |
| 40-50 | 42 | 45 | 1890 |
| 50-60 | 20 | 55 | 1100 |
| 60-70 | 6 | 65 | 390 |
| Σf = 100 | Σfx = 4460 |
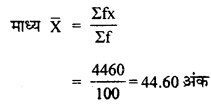
यहाँ सबसे अधिक बारम्बारता 42 समूह (40-50) की है

बहुलक = 43.89
अत: अभीष्ट बहुलक = 43.89 अंक
![]()
We hope the RBSE Class 10 Maths Board Paper 2018 will help you. If you have any query regarding Rajasthan RBSE Class 10 Maths Board Paper 2018, drop a comment below and we will get back to you at the earliest.