RBSE Class 10 Maths Model Paper 1 English Medium

RBSE Class 10 Maths Model Paper 1 English Medium are part of RBSE Class 10 Maths Board Model Papers. Here we have given RBSE Class 10 Maths Sample Paper 1 English Medium.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 10
Subject	Maths
Paper Set	Model Paper 1
Category	RBSE Model Papers

RBSE Class 10 Maths Sample Paper 1 English Medium

Time: 3.15 Hours
Maxim Marks: 80

General Instructions to the Examinees:

1. Candidate must write first his/her Roll on the question paper compulsory.
2. All the questions are compulsory.
3. Write the answer to each question in the given answer sheet only.
4. For question having more than one part, the answers to those parts are to be written together in continuity.
5. If there is any error/difference/contradiction in Hindi & English versions of the question paper, the question of Hindi versions should be treated valid.

6. Part	No.of Question	Marks per Question
   A	1 – 10	1
   B	11 – 15	2
   C	16 – 25	3
   D	26 – 30	6

7. There are internal choices in Q. No. 27 and Q.No 29
8. Write on both sides of the pages of your answer-book. If any rough work is to be done, do it on last pages of the answer-book and cross with slant lines and write ‘Rough Work’ on them.
9. Draw the graph of Question No. 26 on graph paper.

Section – A

Question 1.
Find the value of 588 512 by using ‘Ekaadhiken Purven Sutra’. [1]

Question 2.
Solve
\(\frac { 1 }{ x-1 } + \frac { 1 }{ x-4 } = \frac { 1 }{ x-2 } + \frac { 1 }{ x-3 }\) [1]

Question 3.
After how many digits, decimal expansion of rational number \(\frac{37}{2 \times 5^{2}}\) terminates? [1]

Question 4.
Find the value of tan 52° tan 38° [1]

Question 5.
Find the angle of elevation of the sun. If length of shadow of a tower is equal to its height. [1]

Question 6.
Write the locus of the tip of second’s hand in a clock. [1]

Question 7.
Write the number of circles passing through three non-collinear points. [1]

Question 8.
Find the probability of getting a prime number on throwing a die once. [1]

Question 9.
What is the shape of red signal light in traffic Signs? [1]

Question 10.
Write the equation of “Stopping Sight Distance”. [1]

Section-B

Question 11.
Find square root of 7225 by “Dhunda Yog Method”. [2]

Question 12.
Find the greatest number which divided 247 and 2055 leaving remainders 7 in each case. [2]

Question 13.
Find the area of shaded portion in the given figure. [2]

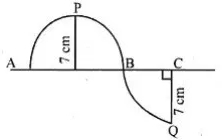
Question 14.
Find the volume of the largest right circular cone that can be cut out of a cube of edge 42 cm. [2]

Question 15.
A CCTV camera is placed on the top of a straight 12 meters high pole in such a way that traffic can be seen beyond 13 meters of line of sight of it. Find the distance from the foot of pole beyond which the traffic is visible. [2]

Section-C

Question 16.
Find a quadratic polynomials whose sum and product of zeroes are 8 and 12 respectively. [3]

Question 17.
Find sum of first 15 terms of an A.P. whose nth term is given by a_n = 25 – 2n. [3]

Question 18.
The angle of elevation of the top of the tower from two points C and D at a distance of x and y from the base of the tower in the same straight line with it are complementary. Prove that the height of the tower is \(\sqrt { xy }\). [3]

Question 19.
Medians of a AABC and AD, BE and CF passes through a point G If AG=5 cm, BE = 12 cm and FG = 3 cm then find AD, GE and GC. [3]

Question 20.
In the given figure PQ and RS are parallel, Prove that ΔPOQ ∼ ΔSOR [3]

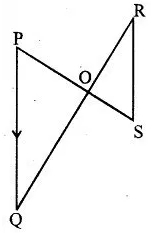
Question 21.
In figure ABCD is a cycle quadrilateral. Find the value of a and b. [3]

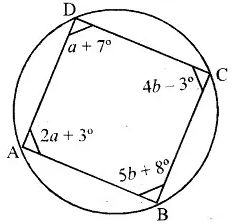
Question 22.
Draw a pair of tangents to a circle of radius 4 cm. Which are inclined to each other at an angle of 70°. [3]

Question 23.
Circumference of a circle is equals to the perimeter of a square, if the area of a square is 484 sq. meter, then find the area of the circle. [3]

Question 24.
The ratio of surface areas of two spheres is 9 : 16 find the ratio of their volumes. [3]

Question 25.
A card is drawn from a well shuffled pack of 52 cards. Find the probability of the following that card is [3]

1. Black
2. Ace of heart
3. Spade

Section-D

Question 26.
Solve the following pair of linear equations by graphical method and find value of ‘a’ where as
4x + 3y = a, x + 3y = 6; 2x – 3y = 12 [6]

Question 27.

1. Prove that cos⁴θ + sin⁴θ = 1 – 2cos² θ sin²θ
2. prove that \(\frac { 1+{ tan }^{ 2 }A }{ 1+{ cot }^{ 2 }A } =[\frac { 1-tanA }{ 1-cotA } ]^{2}\) [0≤A<45°] [6]

OR

1. Prove that \(\sqrt { (\frac { sec\theta +1 }{ sec\theta -1 } ) } = cot\theta + cosec\theta\)
2. If \(\frac {cosA}{cosB}\) = m and  \( \frac {cosA}{cosB}\) = n, then prove that (m² + n²)cos²B =n²

Question 28.
Vertices of the triangle ABC are A (3, -2), B (0, 6) and C (-2, 4), then find the length of its medians. [6]

Question 29.
Prove that the ratio of the areas of two similar triangles is equal to the ratio of square of their corresponding sides. [6]

OR

If a point D on the side BC of an equilateral triangles ABC such that BD = \(\frac {1}{3}\) BC, then prove that 9AD² = 7AB².

Question 30.
Find the mean and median of given frequency distribution. [6]

C.I	0-8	816	16-24	24-32	32-40	40-48
fi	42	30	50	22	8	5

We hope the given RBSE Class 10 Maths Model Paper 1 English Medium will help you. If you have any query regarding RBSE Class 10 Maths Sample Paper 1 English Medium, drop a comment below and we will get back to you at the earliest.