RBSE Class 10 Maths Model Paper 1 are part of RBSE Class 10 Maths Board Model Papers. Here we have given RBSE Class 10 Maths Sample Paper 1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Paper Set | Model Paper 1 |
| Category | RBSE Model Papers |
RBSE Class 10 Maths Sample Paper 1
पूर्णाक: 80 अंक
अवधि: 3 घण्टे 15 मिनट
परीक्षार्थियों के लिए सामान्य निर्देश :
General Instructions to the Examinees :
- परीक्षार्थी सर्वप्रथम अपने प्रश्न-पत्र पर नामांक अनिवार्यतः लिखें।
Candidate must write first his/her Roll No. on the question paper compulsorily. - सभी प्रश्न करने अनिवार्य हैं।
All the questions are compulsory. - प्रत्येक प्रश्न का उत्तर दी गई उत्तर-पुस्तिका में ही लिखें।
Write the answer to each question in the given answer book only. - जिन प्रश्नों में आन्तरिक खण्ड हैं, उन सभी के उत्तर एक साथ ही लिखें।
For questions having more than one part the answers to those parts are to be written together in continuity. - प्रश्न-पत्र के हिन्दी व अंग्रेजी रूपान्तर में किसी प्रकार की त्रुटि/अन्तर/विरोधाभास होने पर हिन्दी भाषा के प्रश्न को ही सही मानें
If there is any error/difference contradiction in Hindi & English versions of the question paper, the question of Hindi version should be treated valid. -
खण्ड प्रश्न संख्या अंक प्रत्येक प्रश्न अ 1-10 1 ब 11-15 2 स 16-25 3 द 26-30 6 Section Q. No. Marks per question A 1-10 1 B 11-15 2 C 26-25 3 D 26-30 6 - प्रश्न संख्या 27 और 29 में आन्तरिक विकल्प हैं।
There are internal choices in Q. No. 27 and 29. - अपनी उत्तर-पुस्तिका के पृष्ठों के दोनों ओर लिखिए। यदि कोई रफ कार्य करना हो तो उत्तर-पुस्तिका के अन्तिम पृष्ठों पर करें और इन्हें तिरछी लाइनों से काटकर उन पर ‘रफ कार्य’ लिख दें।
Write on both sides of the pages of your answer-book. If any rough works is to be done, do it on last pages of the answer-book and cross with slant lines and write ‘Rough Work’ on them. - प्रश्न संख्या 26 का लेखाचित्र माफ पेपर पर बनाना है।
Draw the graph of Q. No. 26 on the graph paper,
खण्ड-अ
[SECTION-A]
प्रश्न 1.
सूत्र ‘एकाधिकेन पूर्वेण’ का प्रयोग करते हुए 588 × 512 का मान ज्ञात कीजिए।
प्रश्न 2.
हल कीजिए:\(\frac { 1 } { x – 1 } + \frac { 1 } { x – 4 } = \frac { 1 } { x – 2 } + \frac { 1 } { x – 3 }\)
प्रश्न 3.
परिमेय संख्या \(\frac { 37 } { 2 \times 5 ^ { 2 } }\) के दशमलव प्रसार में दशमलव के कितने अंकों के पश्चात् अन्त होगा?
![]()
प्रश्न 4.
tan 52°, tan 38° का मान ज्ञात कीजिए।
प्रश्न 5.
यदि एक मीनार की परछाई की लम्बाई मीनार की ऊँचाई के बराबर हो तो सूर्य का उन्नयन कोण ज्ञात कीजिए।
प्रश्न 6.
एक घड़ी में सेकण्ड की सुई के सिरे का बिन्दुपथ लिखिए।
प्रश्न 7.
तीन असरेखीय बिन्दुओं से गुजरने वाले वृत्तों की संख्या लिरिवार
प्रश्न 8.
एक पासे की एक फेंक में अभाज्य संख्या आने की प्रायिकता ज्ञात कीजिए।
प्रश्न 9.
यातायात संकेतों में लाल बत्ती की कैसी ज्यामिति आकृति होती है।?
![]()
प्रश्न 10.
“रोक दृष्टि दूरी” का समीकरण लिखिए।
खण्ड–ब
प्रश्न 11.
“द्वन्द्व योग विधि से 7225 का वर्गमूल ज्ञात कीजिए।
प्रश्न 12.
वह सबसे बड़ी संख्या ज्ञात कीजिए जो 247 और 2055 को इस प्रकार विभाजन करती है कि प्रत्येक स्थिति में शेषफल 7 प्राप्त हो।
प्रश्न 13.
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
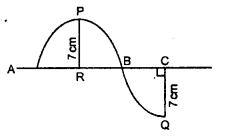
प्रश्न 14.
42 सेमी. कोर के घन से बड़े से बड़ा लम्बवृत्तीय शंकु काटा जाता है शंकु का आयतन ज्ञात कीजिए।
प्रश्न 15.
एक सीधे व 12 मीटर ऊँचे पोल के शीर्ष पर एक CCTV कैमरा लगा है ताकि पोल के शीर्ष से 13 मीटर दूर दृष्टि रेखा के आगे भी यातायात देखा जा सके। इस स्थिति में पोल के पाद से वह दूरी, जिसके आगे से यातायात दिखाई देता है ज्ञात कीजिए।
खण्ड़-स
प्रश्न 16.
एक द्विघात बहुपद ज्ञात कीजिए जिसके शून्यकों का योग तथा गुणनफल क्रमशः 8 व 12 है।
![]()
प्रश्न 17.
किसी समान्तर श्रेणी के प्रथम 15 पदों का योग ज्ञात कीजिए, जिसका n वाँ पद an = 25 – 2n है।
प्रश्न 18.
किसी मीनार के आधार से और y दूरी पर एक ही रेखा पर स्थित दो बिन्दुओं क्रमशः C व D से देखने पर मीनार के शिखर के उन्नयन कोण एक-दूसरे के पूरक हैं। सिद्ध कीजिए कि मीनार की ऊँचाई \(\sqrt { x y }\) हैं।
प्रश्न 19.
एक ∆AEC की माध्यिकाएँ AD, BE और CF एक बिन्दु G से गुजरती हैं। यदि AG = 5 सेमी., BE = 12 सेमी. और FG = 3 सेमी हो तो AD, GE और GC ज्ञात कीजिए।
प्रश्न 20.
दी गई आकृति में PQ और RS समान्तर हैं तो सिद्ध कीजिए
∆POQ ~ ∆SOR
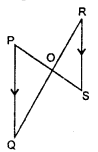
प्रश्न 21.
आकृति में ABCD एक चक्रीय चतुर्भुज है a और b का मान ज्ञात कीजिए।
प्रश्न 22.
एक 4 सेमी त्रिज्या का वृन खींचिए उस पर दो स्पर्श रेखाएँ इस प्रकार खींचिए कि ये परस्पर 70° का कोण बनाती हों।
![]()
प्रश्न 23.
एक वृत्त की परिधि एक वर्ग के परिमाप के बराबर है, यदि वर्ग का क्षेत्रफल 484 वर्ग मीटर हो तो वृत्त का क्षेत्रफल ज्ञात कीजिए।
प्रश्न 24.
दो गोलों के पृष्ठीय क्षेत्रफलों का अनुपात 9 : 16 है। उनके आयतनों का अनुपात ज्ञात कीजिए।
प्रश्न 25.
52 पत्तों की अच्छी प्रकार से फेंटी गई एक गडी में से एक पत्ता निकाला जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए कि पत्ता
(1) काले रंग का है
(2) पान का इक्का है
(3) हुकुम का है
खण्डु – द
प्रश्न 26.
निम्न रैखिक समीकरण युग्म को आलेखीय विधि से हल कीजिए तथा इसकी सहायता से ‘a’ का मान ज्ञात कीजिए जबकि 4x + 3y = a हैं।
x + y = 6;
2x – 3y = 12
प्रश्न 27.
(i) सिद्ध कीजिए
cos4θ + sin4θ = 1 – 2cos2θ sin2θ
(ii) सिद्ध कीजिए
\(\left( \frac { 1 + \tan ^ { 2 } A } { 1 + \cot ^ { 2 } A } \right) = \left( \frac { 1 – \tan A } { 1 – \cot A } \right) ^ { 2 } = \tan ^ { 2 } A\)
अथवा
(i) सिद्ध कीजिए: \(\sqrt { \left( \frac { \sec \theta + 1 } { \sec \theta – 1 } \right) } = \cot \theta + \csc \theta\)
(ii) यदि \(\frac { \cos A } { \cos B } = m\) तथा \(\frac { \cos A } { \sin B } = n\) हो तो सिद्ध कीजिए
(m2 +n2) cos2 B = n2
प्रश्न 28.
त्रिभुज ABC की माध्यिकाओं की लम्बाई ज्ञात कीजिए। | जिसके शीर्ष A (3,-2), B (0, 6) और (C (-2, 4) हैं।
![]()
प्रश्न 29.
सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के समान होता है।
अथवा
किसी समबाहु त्रिभुज ABC की भुजा EC पर एक बिन्दु D इस प्रकार स्थित है कि \(\mathbf { B D } = \frac { 1 } { 3 } \mathbf { B C }\) है, तो सिद्ध कीजिए।
9AD2 = 7 AB2
प्रश्न 30.
निम्न बारम्बारता बंटन के माध्य व माध्यिका ज्ञात कीजिए
| वर्ग | 0 – 8 | 8 – 16 | 16 – 24 | 24 – 32 | 32 – 40 | 40 – 48 |
| fi | 42 | 30 | 50 | 22 | 8 | 5 |
हल
हल 1:
\(588 \times 512 = \frac { 5 \times 6 } { 88 \times 12 } = \frac { 30 } { 1056 } = 3,01,056\)
हल 2:
वाम पक्षों के हरों का योग = x – 1+ x – 4 = 2x – 5
दक्षिण पक्ष के हरों का योग = x – 2 + x – 3 = 2x – 5
अतः 2x -5 = 0 या 2x =5
\(\therefore \quad x = \frac { 5 } { 2 }\)
हल 3:
\(\frac { 37 } { 2 \times 5 ^ { 2 } } = \frac { 37 \times 2 } { 2 \times 5 ^ { 2 } \times 2 } = \frac { 74 } { 2 ^ { 2 } \times 5 ^ { 2 } } = \frac { 74 } { 10 ^ { 2 } } = 0 \cdot 74\)
अर्थात् \(\frac { 37 } { 2 \times 5 ^ { 2 } }\) के दशमलव प्रसार में दशमलव के दो अंकों के पश्चात् अन्त होगा
हल 4:
tan 52° . tan 38° = tan 52° . tan (90° – 52°)
= tan 52° . cot 52
\(= \tan 52 ^ { \circ } \times \frac { 1 } { \tan 52 ^ { \circ } } = 1\)
![]()
हल 5:
माना मीनार की ऊँचाई h मी. है तो परछाई की लम्बाई भी h मी. होगी।
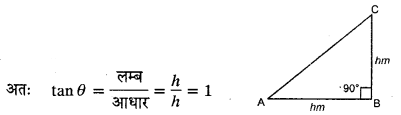
∴ θ = 45°
अर्थात् सूर्य का उन्नयन कोण 45° होगा
हल 6:
एक घड़ी में सेकण्ड की सुई के सिरे का बिन्दुपथ एक वृत्त होगा।
हल 7:
तीन असंरेखीय बिन्दुओं से गुजरने वाले वृत्तों की संख्या एक होगी।
हल 8:
एक पासे को यादृच्छया फेंके जाने पर प्राप्त होने वाले सभी
सम्भव परिणामों की संख्या S = {1, 2, 3, 4, 5, 6}
यहाँ पर अभाज्य संख्याएँ E = {2, 3, 5}

![]()
हल 9:
यातायात संकेतों में लाल बत्ती की आकृति अष्टभुजा वाली होती
हल 10:
रोक दृष्टि दूरी = प्रतिक्रिया दूरी + अवरोध दूरी
हल 11:
द्वन्द्व योग विधि
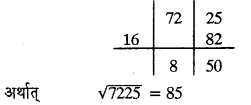
हल 12:
दिया है कि 2055 को अभीष्ट पूर्णाक से विभाजित करने पर शेषफले 7 रह जाता है। ∴ 2055 -7 = 2048 को अभीष्ट संख्या पूर्णतः विभाजित करती है। इसी प्रकार 247 -7 = 240 भी अभीष्ट संख्या से विभाज्य है। अब 2048 व 240 का महत्तम समापवर्तक ज्ञात करने पर
2048 = 240 × 8 + 128
240 = 128 × 1 + 112
128 = 112 × 1 + 16
112 = 16 × 7 + 0
अर्थात् वह सबसे बड़ी संख्या 112 है।
हल 13:
प्रश्नानुसार त्रिज्या (r) = 7 cm
अत: छायांकित भाग का क्षेत्रफल \(= \frac { \pi r ^ { 2 } } { 2 } + \frac { \pi r ^ { 2 } } { 4 } = \frac { 3 } { 4 } \pi r ^ { 2 }\)
\(= \frac { 3 } { 4 } \times \frac { 22 } { 7 } \times 7 \times 7\)
= 115.5cm2
![]()
हल 14:
प्रश्नानुसार त्रिज्या (r) = 21 सेमी. तथा ऊँचाई (h) = 42 सेमी.
∵ आयतन (V) \(= \frac { 1 } { 3 } \pi r ^ { 2 } h\)
\(= \frac { 1 } { 3 } = \frac { 22 } { 7 } \times 21 \times 21 \times 42\)
= 22 × 7 × 21 × 6 = 19,404 घन सेमी.
हल 15:
पाइथागोरस प्रमेय से
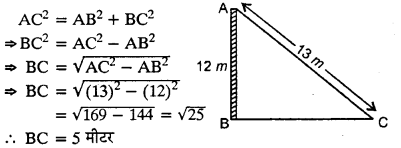
अतः पोल के पाद से 5 मीटर की दूरी के आगे का यातायात दिखाई देगा।
हल 16:
शून्यकों का योग = 8
तथा शून्यकों का गुणनफल = 12
अर्थात् α +β = 8
तथा αβ = 12
∴ x2 – (α + β)x + αβ
⇒ x2 – (8)x+ 12 = x2 – 8x + 12
हल 17:
प्रश्नानुसार, an = 25 – 21
∴ a1 = 25 – 2(1) = 25 – 2 = 23
a2= 25 – 2 (2) = 25 – 4 = 21
a3 = 25 -2 (3) = 25 – 6 = 19
अर्थात् यहाँ a = 23 तथा d = -2
∴ योग (Sn)\(= \frac { 15 } { 2 } [ 2 ( 23 ) + 14 ( – 2 ) ]\)
\(= \frac { 15 } { 2 } [ 46 – 28 ] = \frac { 15 } { 2 } \times 18 = 15 \times 9 = 135\)
हल 18:
माना मीनार की ऊँचाई AB = h मीटर तथा C व D पर बिन्दु इस प्रकार है कि BC = x तथा BD = b यदि ∠ACB = 8 हो तो
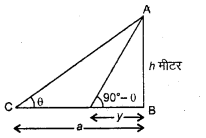
∠ADB = 90° – θ
अब समकोण त्रिभुज ABC में
\(\tan \theta = \frac { \mathrm { AB } } { \mathrm { BC } } = \frac { h } { x }\) ……………. (i)
पुनः समकोण ∠ABD में
\(\tan \left( 90 ^ { \circ } – \theta \right) = \frac { \mathrm { AB } } { \mathrm { BD } }\)
या \(\cot \theta = \frac { h } { y }\) ……………………… (ii)
समी. (i) व (ii) का गुणा करने पर
\(\tan \theta \times \cot \theta = \frac { h } { x } \times \frac { h } { y }\) या \(1 = \frac { h ^ { 2 } } { x y }\)
⇒ h2 = xy
या \(h = \sqrt { x y }\)
अतः मौनार की ऊँचाई \(\sqrt { x y }\) मीटर है।
![]()
हल 19:
हम जानते हैं कि बिन्दु G माध्यिकाओं को 2 : 1 में अन्तः विभाजित करता है।
\(\therefore \frac { \mathrm { AG } } { \mathrm { GD } } = \frac { 2 } { 1 }\) या \(\frac { \mathrm { GD } } { \mathrm { AG } } = \frac { 1 } { 2 }\)
दोनों ओर 1 जोड़ने पर
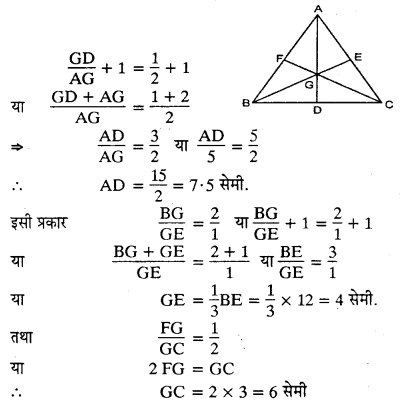
हल 20:
PQ || RS (दिया है)
अतः ∠P = ∠S (एकान्तर कोण)
और ∠Q = ∠R (एकान्तर कोण)
साथ ही ∠POQ = ∠SOR (शौर्षाभिमुख कोण)
इसलिए ∆POQ ~ ∠SOR (AAA समरूपता कसौटी)
इति सिद्धम्
हल 21:
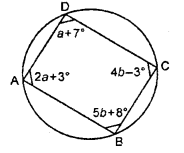
हम जानते हैं कि एक चक्रीय चतुर्भुज के सम्मुख कोण सम्पूरक होते हैं।
2B + 2D = 180° a +7 + 55 + 5 = 180
∴ ∠B + ∠D = 180°
⇒ a + 7 + 5b + 8 = 180
⇒ a + 5b = 180 – 15 = 165
या a + 5b = 165 ………………….. (i)
तथा ∠A + ∠C = 180°
⇒ 2a + 3 + 4b – 3 = 180
⇒ 2a + 4b = 180
⇒ 2a + 4b = 180° …………………….. (ii)
सनी. (i) व (ii) को हल करने पर a = 40° तथा b = 25°
हल 22:
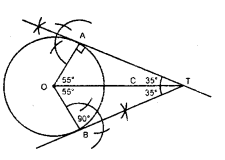
रचना के पद
- केन्द्र ‘O’ लेकर 4 सेमी.4 त्रिज्या का वृत्त बनाइये
- बिन्दु ‘O’ पर दोनों तरफ 55° के कोण बनाइये।
- वृत्त को A व B बिन्दु पर काटते हैं। OA व OB को मिलाइये
- विन्दु A व B पर स्पर्श रेखा की रचना कीजिये
- स्पर्श रेखाएँ बिन्दु T पर मिलती है
- कोण BTA को नापिये।
∠BTA = 70°
नोट- चतुर्भुज के चारों कोगों का योग 360° होता है।
अतः ∠AOB = 360° – 90° – 90° – 70° = 110°
∠AOT = ∠BOT = 35° बनायें।
![]()
हल 23:
वर्ग का क्षेत्रफल = 484 वर्ग मीटर
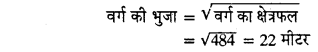
प्रश्नानुसार, वृत्त की परिधि = वृत्त का परिमाप
2πr = 4 × भुजा
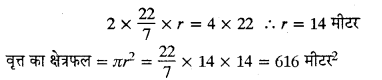
हल 24:
हम जानते हैं कि
गोले का पृष्ठीय क्षेत्रफल = 4πr2

हल 25:
पत्तों की कुल संख्या = 52
(1) काले रंग के कुल पते = 26
∴ काले रंग के पत्ते को प्राप्त करने की प्रायिकता \(= \frac { 26 } { 52 } = \frac { 1 } { 2 }\)
(2) पान के इक्कों की संख्या = 1
अतः पान के इक्के को प्राप्त करने की प्रायिकता \(= \frac { 1 } { 52 }\)
(3) हुकुम के पत्तों की संख्या = 13
हुकुम का पत्ता प्राप्त करने की प्रायिकता \(= \frac { 13 } { 52 } = \frac { 1 } { 4 }\)
![]()
हल 26:
समीकरण x + 3y = 6 द्वारा निरूपित रेखा का आलेखन दिया है
x + 3y = 6 ⇒ x = 6 – 3y
y = 1 रखने पर = 6 – 3 × 1 = 6 – 3 = 3
तथा y = 2 रखने पर x = 6, – 3 × 2 = 6 = 6 = 0
अतः समीकरण x + 3y = 6 को निम्न हल सारणी प्राप्त होती है
| x | 3 | 0 |
| y | 1 | 2 |
बिन्दुओं A (3, 1) व B (0, 2) को ग्राफ पेपर पर अंकित करके इनसे गुजरने वाली रेखा AB खींचते हैं कि समीकरण x + 3y = 6 का आलेख
हैं।
समीकरण 2x – 3y = 12 द्वारा निरूपित रेखा का आलेखन
2x – 3y = 12 ⇒ 3y = 2x – 12
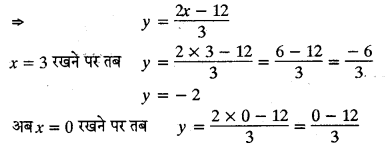
\(y = \frac { – 12 } { 3 } = – 4\)
अतः समीकरण 2x – 3y = 12 का निम्न हल सारणी में प्राप्त होता हैं
| x | 3 | 0 |
| y | -2 | -4 |
बिन्दुओं c (3 – 2) तथा D (0, -4) को उसी प्राफ पर प्रदर्शित करते हुए उनसे गुजरने वाली रेखा CD खींचते हैं जो कि समीकरण 2x – 3y = 12 का माफ दर्शाती है। माफ से स्पष्ट है कि दोनों समीकरणों के संगत सरल रेखाएँ एक-दूसरे को बिन्दु P (6, 0) पर काटती हैं।
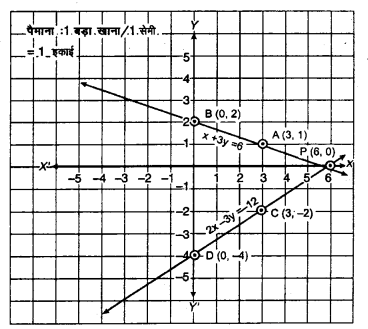
अतः x = 6 तथा y = 0 दिये गये समीकरण युग्म का हल है।
4x + 3y = a में x = 6 व y = 0 रखने पर
4 × 6 + 3 × 0 = a ⇒ a = 24
![]()
हल 27:
(i) L.H.S.
= cos4θ + sin4θ (2 sin2θ cos2θ) से जोड़ने व घटाने पर
= cos4θ + sin4θ + 2 sin2θcos2θ – 2sin2θcos2θ
= (sin4θ + cos4θ + 2sin2θcos2θ)- 2 sin2θcos2θ
= (sin2θ + c0s2θ) – 2 sin2θcos2θ
= (1)2 – 2 sin2θcos2θ [∵ sin2θ + cos2θ = 1]
=1- 2 sin 2θcos2θ = R.H.S.
∴ L.H.S. = R.H.S.
(ii) L.H.S(वाम पक्ष)
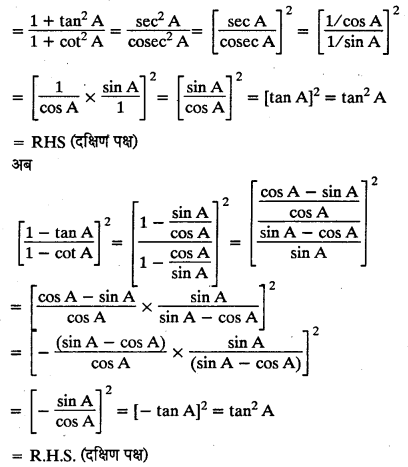
अथवा
(i) L.H.S. = \(\sqrt { \frac { \sec \theta + 1 } { \sec \theta – 1 } }\)
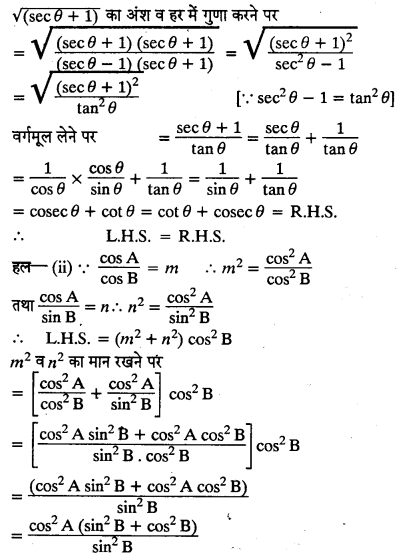
\(= \frac { \cos ^ { 2 } \mathbf { A } } { \sin ^ { 2 } \mathbf { B } } \times 1 \quad \left[ \because \sin ^ { 2 } \mathbf { B } + \cos ^ { 2 } \mathbf { B } = 1 \right]\)
\(= \frac { \cos ^ { 2 } A } { \sin ^ { 2 } B } = n ^ { 2 } = R . H . S\)
∴ L.H.S. = R.H.S.
![]()
हल 28:
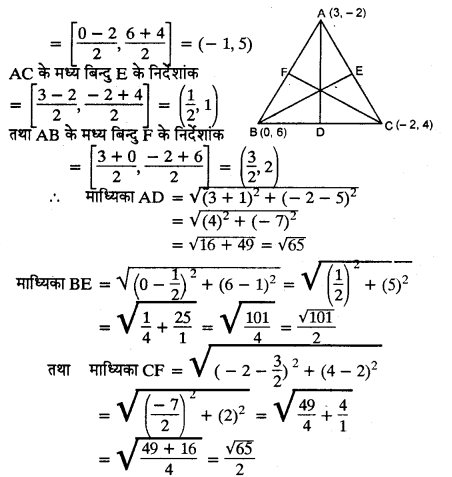
हल 29:
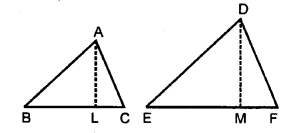
दिया हुआ है- ∆ ABC एवं ∆DEF में ∆ABC ~ ∆DEF है।
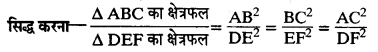
रचना- AL ⊥ BC एवं DM ⊥ EF खींचा
उपपति- ∵ ∆ABC ~ ∆DEF
∴ ∠A = ∠D, ∠B = ∠E
और ∠C = ∠F
एवं \(\frac { \mathrm { AB } } { \mathrm { DE } } = \frac { \mathrm { BC } } { \mathrm { EF } } = \frac { \mathrm { CA } } { \mathrm { FD } }\) ………….. (1)
∆ ALB व ∆ DME में ……………… (2)
∠ALB = ∠DME (प्रत्येक कोण 90°)
∠B = ∠E (1 के द्वारा)
अतः ∆ ALB ~ ∆ DME (A-A समरूपता प्रमेय द्वारा)

अथवा
हल:
∵ ∆ ABC एक समबाहु त्रिभुज है और A से BC पर लम्य डाला जाता है। हम जानते हैं कि किसी भी शीर्ष से सम्मुख मुजा पर डाला गया लम्ब उसका समद्विभाजन करता है।
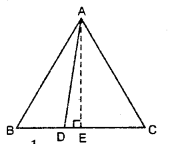

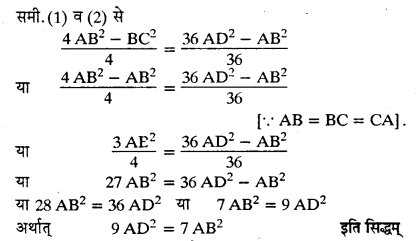
![]()
हल 30:
| वर्ग अन्तराल | बारम्बारता | मध्यमान | fi × xi |
| 0 – 8 | 42 | 4 | 168 |
| 8 – 16 | 30 | 12 | 360 |
| 16 – 24 | 50 | 20 | 1000 |
| 24 – 32 | 22 | 28 | 616 |
| 32 – 40 | 8 | 36 | 288 |
| 40 – 48 | 5 | 44 | 220 |
| N = Σf = 157 | Σ xi × fi = 2652 |
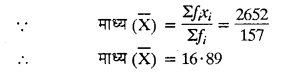
संचयी बारम्बारता सारणी
| वर्ग | f | c.f. |
| 0 – 8 | 42 | 42 |
| 8 – 16 | 30 | 72 |
| 16 – 24 | 50 | 122 |
| 24 – 32 | 22 | 144 |
| 32 – 40 | 8 | 152 |
| 40 – 48 | 5 | 151 |
| N = Σf = 157 |
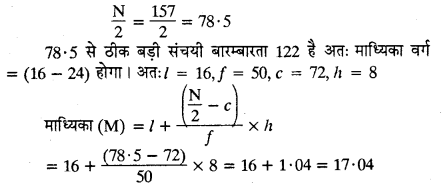
![]()
We hope the RBSE Class 10 Maths Model Paper 1 will help you. If you have any query regarding RBSE Class 10 Maths Sample Paper 1, drop a comment below and we will get back to you at the earliest.