RBSE Class 10 Maths Model Paper 2 English Medium

RBSE Class 10 Maths Model Paper 2 English Medium are part of RBSE Class 10 Maths Board Model Papers. Here we have given RBSE Class 10 Maths Sample Paper 2 English Medium.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 10
Subject	Maths
Paper Set	Model Paper 2
Category	RBSE Model Papers

RBSE Class 10 Maths Sample Paper 2 English Medium

Time: 3.15 Hours
Maxim Marks: 80

General Instructions to the Examinees:

1. Candidate must write first his/her Roll on the question paper compulsory.
2. All the questions are compulsory.
3. Write the answer to each question in the given answer sheet only.
4. For question having more than one part, the answers to those parts are to be written together in continuity.
5. If there is any error/difference/contradiction in Hindi & English versions of the question paper, the question of Hindi versions should be treated valid.

6. Part	No.of Question	Marks per Question
   A	1 – 10	1
   B	11 – 15	2
   C	16 – 25	3
   D	26 – 30	6

7. There are internal choices in Q. No. 27 and Q.No 29
8. Write on both sides of the pages of your answer-book. If any rough work is to be done, do it on last pages of the answer-book and cross with slant lines and write ‘Rough Work’ on them.
9. Draw the graph of Question No. 26 on graph paper.

Part – A

Question 1.
Solve  \(\frac {1}{x+4} + \frac {1}{x-6} = 0\)  using vedic method. [1]

Question 2.
Find cube root of 493039. 01 [1]

Question 3.
If two numbers are written in the form. m = pq³ and n = p³q², then what is the HCF of m and n where p and q are prime numbers. [1]

Question 4.
Evaluate \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\) [1]

Question 5.
Evaluate \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\) [1]

Question 6.
If in the figure, AB = 3.4cm, BD = 4cm, BC = 10cm, AD is internal bisector of ∠A, then find the measure of AC. [1]

Question 7.
In which triangle the orthocentre is its vertex? [1]

Question 8.
If marks obtained by 10 Students of a class in mathematics are 52,75,40,70,43,40,65,35,48,52 then find A.M. [1]

Question 9.
If a CCTV camera is mounted on a pole, What is the name of the area of surveillance of the Camera around the pole? [1]

Question 10.
A CCTV Camera is mounted at the top of a 24 m pole. The Camera can be visible up to a distance of 25 m from the top of the pole.

Find the area of green patch around the pole. (π = \(\frac{22}{7}\)) [1]

Part – B

Question 11.
Solve \(\frac{1}{x+7} + \frac{1}{x+9} = \frac{1}{x+6} + \frac{1}{x+10}\) [2]

Question 12.
If HCF of numbers 408 and 1032 is expressed in the form of 1032x – 408 × 5 then find the value of x. [2]

Question 13.
The radius of a semi-circular plot is 21 meter. Find its area and perimeter. [2]

Question 14.
Find the volume of a right circular cone whose radius of the base is 6 cm and height is 7 cm. [2]

Question 15.
A CCTV camera is fixed on a pole 5 meter high which keeps surveillance up to 13 meter distance. Find the area the camera can see around the pole. [2]

Part – C

Question 16.
The product of two expressions is (x – 7) (x² + 8x + 12). If their highest common factor (HCF) is x + 6, then find their LCM. [3]

Question 17.
Give the geometrical interpretation of nature of solution of the pair of linear equations 2x – y = 4, x + y = -1 [3]

Question 18.
Prove that (secθ – tanθ)² =\(\frac{1-\sin \theta}{1+\sin \theta}\) [3]

Question 19.
In ΔABC, the medians AD, BE and CF passes through the point G. If GF = 4cm, then find GC and if AD = 7.5cm, then find GD. [3]

Question 20.
If ΔABC ~ ΔDEF in which AB = 2.2 cm and DE = 3.3cm, find this ratio of the areas of ΔABC and ΔDEF. [3]

Question 21.
In the given figure, find the value of x in terms of a, b and c. [3]

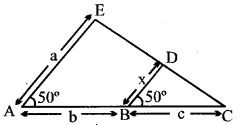
Question 22.
Find the area of the shaded portion in the following figure which is the region between the two quadrants of the circle of radius 8 cm each. [3]

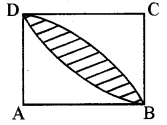
Question 23.
The left part of a solid body is cylindrical and right part is conical if the diameter of the cylinder is 14 cm and its length is 40 cm and the diameter of the cone is 14 cm and its height is 12 cm. Find the volume of the solid. [3]

Question 24.
If O is centre of ΔABC, then prove that ∠OBC + ∠BAC = 90° [3]

Question 25.
Find the probability that a common year (not a leap year) contains only 52 Sundays. [3]

Part – D

Question 26.
Solve the quadratic equation 9x² – 9(a + b)x+(2a² + 5ab + 2b²) = 0 by Shridhar Acharya quadratic formula. [6]

Question 27.
From base of a incomplete tower at a distance 120 meter, from a point, elevation angle of top of tower is 30°. Determine what must be height of tower for elevation angle 60° on same place. [6]

OR

A tower and a building are situated on the opposite side of a road. The angles of depression from the top of tower at the roof and base of the building are 45° and 60° respectively. If height of the building is 12m, then find the height of the tower (\(\sqrt{3}\) = 1.732)

Question 28.
If point (x, y) lies at equal distance from points (a + b, b – a) and (a – b, a + b), then prove that bx = ay. [6]

Question 29.
Diagonals of a quadrilateral ABCD, intersect each other at the point O such that \(\frac{AO}{BO} = \frac{CO}{DO}\)
Prove that ABCD is a trapezium. [6]

OR

If the medians of a triangle are equal, then prove that it is equilateral.

Question 30.
Find the mean of following distribution by step deviation method. [6]

Weight (in Kg)	40-50	50-60	60-70	70-80	80-90	90-100
No of students	10	25	28	12	10	15

We hope the given RBSE Class 10 Maths Model Paper 2 English Medium will help you. If you have any query regarding RBSE Class 10 Maths Sample Paper 2 English Medium, drop a comment below and we will get back to you at the earliest.