RBSE Class 12 Maths Model Paper 1 English Medium are part of RBSE Class 12 Maths Board Model Papers. Here we have given RBSE Class 12 Maths Sample Paper 1 English Medium.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 12 |
| Subject | Maths |
| Paper Set | Model Paper 1 |
| Category | RBSE Model Papers |
RBSE Class 12 Maths Sample Paper 1 English Medium
Time – 3 ¼ Hours
Maximum Marks: 80
General instructions to the examines
- Candidate must write first his/her Roll No. on the question paper compulsorily.
- All the questions are compulsory
- Write the answer to each question in the given answer book only.
- For questions having more than one part the answers to those parts are to be written together in continuity.
- If there is any error/difference/contradiction in Hindi & English versions of the question paper, the question of Hindi version should be treated valid.
-
Section Q.No Marks for question A 1-10 1 B 11-15 2 C 16-25 3 D 26-30 6 - There are internal choices in Q. No. 16. 21. 24. 28 and 30. You have to attempt only one of the alternatives in these questions.
- Draw the graph of Q.No. 25 on the graph paper.
Section – A
Question 1.
Write composition table for addition S = {(0, 1, 2); +3}. [1]
Question 2.
If \(\cot ^{-1} x+\tan ^{-1}\left(\frac{1}{3}\right)=\frac{\pi}{2}\) then find the value of x. [1]
![]()
Question 3.
![]() [1]
[1]
Question 4.
If points (x, -2), (5, 2), (8, 8) are collinear, then find the value of x. [1]
Question 5.
Find \(\int \log x d x\) [1]
Question 6.
Find the unit vector along the sum of vectors \(a=2 \hat{i}+2 \hat{j}-5 \hat{k}, b=2 \hat{i}+\hat{j}+3 \hat{k}\) [1]
Question 7.
Find the value of \(\left[ \begin{array}{lll}{2 \hat{i}} & {\hat{j}} & {\hat{k}}\end{array}\right]+\left[ \begin{array}{lll}{\hat{i}} & {\hat{j}} & {\hat{k}}\end{array}\right]+\left[ \begin{array}{lll}{\hat{k}} & {\hat{j}} & {2 \hat{i}}\end{array}\right]\) [1]
Question 8.
![]() [1]
[1]
Question 9.
Show the region of feasible solution under the following constraints x + 2y ≤ 8, .x ≥ 0, y ≥ 0 in answer book. [1]
![]()
Question 10.
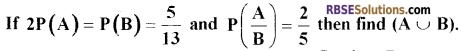 [1]
[1]
Section – B
Question 11.
If function f: R → R, f (x) = 2x + 1 then show that \(\left(f^{-1}\right)^{-1}=f\) [2]
Question 12.
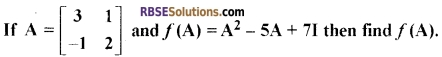 [2]
[2]
Question 13.
Examine Continuity at x = 1 of function f(x) = |x – 1| [2]
Question 14.
Find \(\int \frac{1}{1+\sin x} d x\) [2]
Question 15.
If a vector makes angles α, β, and γ respectively with axes OX, OY, OZ, then prove that sin²α + sin²β + sin²γ = 2. [2]
![]()
Section – C
Question 16.
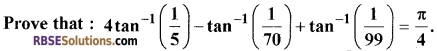 [3]
[3]
OR

Question 17.
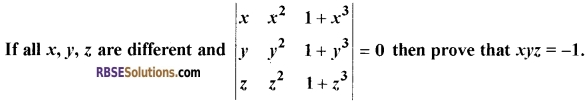 [3]
[3]
Question 18.
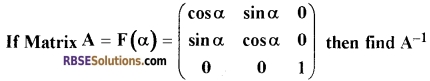 [3]
[3]
Question 19.
Find equation of normal to the curve 2x² – y² = 14 which is parallel to line x + 3y = 6. [3]
Question 20.
Find two positive numbers x and y, sum of them is 60 and xy³ is maximum. [3]
Question 21.
Find \(\int \sqrt{x^{2}+a^{2}} d x\) [3]
OR
Find \(\int \frac{1}{1-6 x-9 x^{2}} d x\)
![]()
Question 22.
Find area of region bounded by curve \(y=2 \sqrt{1-x^{2}}\) and above x-axis. [3]
Question 23.
Find area of region bounded by curve [(x,y)/x² ≤ y ≤ x] [3]
Question 24.
If \(\overline{a}=3 \hat{i}+\hat{j}+2 \hat{k} \text { and } \overline{b}=2 \hat{i}-2 \hat{j}+2 \hat{k}\) then find unit vector \(\hat{n} \) perpendicular both \(\overline{a} \text { and } \overline{b}\) [3]
OR
![]()
Question 25.
By graphical method solve the following linear programming problem for [3]
Maximum z = 2x + 3y
Constraints 4x + 6y ≤ 60, 2x + y ≤ 20 and x ≥ 0, y ≥ 0.
Section-D
Question 26.
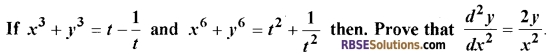 [6]
[6]
Question 27.
Show that \(\int_{0}^{\frac{\pi}{2}} \log \sin x d x=\frac{\pi}{2} \log \frac{1}{2}\) [6]
Question 28.

OR
Find the perticular solution of the differential equation \(\frac{d y}{d x}\) + 2xy = xsin x² If x = 0 and y = 1. [6]
Question 29.
Find the angle between the two lines. These direction-cosines are given by the following relations. l- 5m + 3n = 0 and 7l² + 5m² – 3n² = 0 [6]
![]()
Question 30.
A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six. [6]
OR
Two coins are tossed at the same time. Find the variance of “number of heads”.
We hope the given RBSE Class 12 Maths Model Paper 1 English Medium will help you. If you have any query regarding RBSE Class 12 Maths Sample Paper 1 English Medium, drop a comment below and we will get back to you at the earliest.