RBSE Class 12 Maths Model Paper 2 English Medium are part of RBSE Class 12 Maths Board Model Papers. Here we have given RBSE Class 12 Maths Sample Paper 2 English Medium.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 12 |
| Subject | Maths |
| Paper Set | Model Paper 2 |
| Category | RBSE Model Papers |
RBSE Class 12 Maths Sample Paper 2 English Medium
Time – 3 ¼ Hours
Maximum Marks: 80
General instructions to the examines
- Candidate must write first his/her Roll No. on the question paper compulsorily.
- All the questions are compulsory.
- Write the answer to each question in the given answer book only.
- For questions having more than one part, the answers to those parts are to be written together in continuity.
Section – A
Question 1.
If 3 is identity element of the binary operation on Q defined by a * b = \(\frac{a b}{3}\) find a-1 for a ∈ Q [1]
Question 2.
If sin-1 x + 3cos-1 x = π Find x. [1]
Question 3.
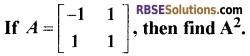 [1]
[1]
![]()
Question 4.
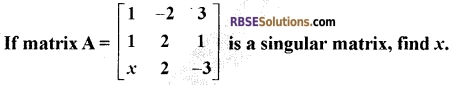 [1]
[1]
Question 5.
Evaluate \(\int \frac{1-\cos 2 x}{1+\cos 2 x} d x\) [1]
Question 6.
Find the position vector of the midpoint of the vector joining the points P(2, 3, 4) and Q(4, 1, -2). [1]
Question 7.
If for a vector \(\vec{a},(\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=12\) the find \(\vec|x|\). [1]
Question 8.
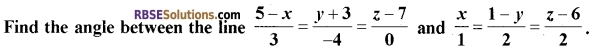 [1]
[1]
Question 9.
Find the feasible region for the following constraint [1]
x + y ≤ 10, x + 2y ≥ 20, x ≥ 0, y ≥ 0
![]()
Question 10.
A pair of dice is thrown 7 times. If getting a total of 7 is a success what is the probability of 6 successes? [1]
Section – B
Question 11.
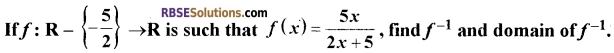 [2]
[2]
Question 12.
 [2]
[2]
Question 13.
Differentiate: logelogex². [2]
Question 14.
Evaluate \(\int \frac{1}{16-9 x^{2}} d x\) [2]
Question 15.
Find a vector perpendicular to the vectors \(4 \hat{i}-\hat{j}+3 \hat{k} \text { and }-2 \hat{i}+\hat{j}-2 \hat{k}\) whose magnitude is 9 unit. [2]
![]()
Section – C
Question 16.
If tan-1x + tan-1y + tan-1z = \(\frac{\pi}{2}\) then prove that xy + yz + zx = 1 [3]
OR
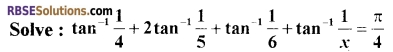
Question 17.
 [3]
[3]
Question 18.
Find k such that the points (k, 2 – 2k), (-k + 1, 2k) and (-4 – k, 6 – 2k) are collinear. [3]
Question 19.
Show that of all the rectangles in a circle, the square has the maximum area. [3]
Question 20.
Find the minimum value of a such that the function f(x) = x² + 9x + 5 is increasing in [1,2] [3]
Question 21.
Find \(\int \frac{d x}{\sqrt{9 x-4 x^{2}}}\) [3]
OR
Evaluate \(\mathrm{I}=\int \frac{\sin x+\cos x}{9+16 \sin 2 x} d x\)
![]()
Question 22.
Find the area enclosed by the lines 2x + y = 4, x = 0, x = 3. [3]
Question 23.
Find the area of the ΔABC using calculus where the vertices are A(2,5), B(4, 7) and C(6, 2). [3]
Question 24.
By vector method prove that the line joining mid points of two sides of a triangle is parallel to third side. [3]
OR
Verify the formula \(\vec{a} \times(\vec{b} \times \vec{c})=(\vec{a} \cdot \vec{c}) \vec{b}-(\vec{a} \cdot \vec{b}) \vec{c}\)
where \(\vec{a}=\hat{i}+\hat{j}-2 \hat{k}, \vec{b}=2 \hat{i}-\hat{j}+\hat{k} \text { and } \vec{c}=\hat{i}+3 \hat{j}-\hat{k}\)
Question 25.
A housewife wishes to mix together two kinds of food, X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contain is of one kg of food are given below : [3]
| Food X | 1 | 2 | 3 |
| Food Y | 2 | 2 | 1 |
One Kg. of food X costs Rs. 6/- and one Kg of food Y costs Rs. 10. Find the least cost of the mixture which will produce the diet.
Section – D
Question 26.
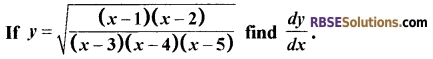 [6]
[6]
Question 27.
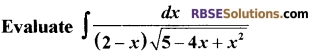 [6]
[6]
![]()
Question 28.
![]()
OR
Solve : (ey+ 1)cosx dx + ey sin x dy = 0 [6]
Question 29.
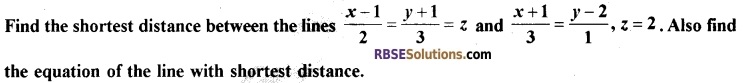 [6]
[6]
Question 30.
A problem in mathematics is given to 3 students whose chances of solving it are a What is the probability that the problem is solved. [6]
OR
Three coins are tossed together. The random variable X be the number of heads on coins. Find mean X.
![]()
We hope the given RBSE Class 12 Maths Model Paper 2 English Medium will help you. If you have any query regarding RBSE Class 12 Maths Sample Paper 2 English Medium, drop a comment below and we will get back to you at the earliest.