RBSE Solutions for Class 10 Maths Chapter 12 वृत्त Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 12 वृत्त Additional Questions.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 12 |
| Chapter Name | वृत्त |
| Exercise | Additional Questions |
| Number of Questions Solved | 108 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 12 वृत्त Additional Questions
विविध प्रश्नमाला 12
वस्तुनिष्ठ प्रश्न (1 से 20 तक)
प्रश्न 1.
10 सेमी. त्रिज्या वाले वृत्त के केन्द्र से 6 सेमी. दूर (RBSESolutions.com) स्थित जीवा की लम्बाई
(क) 16 सेमी.
(ख) 8 सेमी.
(ग) 4 सेमी.
(घ) 5 सेमी.
उत्तर:
(क) 16 सेमी.
प्रश्न 2.
13 सेमी. त्रिज्या वाले वृत्त में 24 सेमी. लम्बी जीवा खींची गई है। जीवा की वृत्त के केन्द्र से दूरी है
(क) 12 सेमी.
(ख) 5 सेमी.
(ग) 6.5 सेमी.
(घ) 12 सेमी.
उत्तर:
(ख) 5 सेमी.
![]()
प्रश्न 3.
लघुचाप का डिग्री माप होता है
(क) 180° से कम
(ख) 180° से अधिक
(ग) 360°
(घ) 270°
उत्तर:
(क) 180° से कम
प्रश्न 4.
दीर्घचाप का डिग्री माप (RBSESolutions.com) होता है
(क) 180° से कम
(ख) 180° से अधिक
(ग) 360°
(घ) 90°
उत्तर:
(ख) 180° से अधिक
प्रश्न 5.
एक वृत्त में केन्द्र से समान दूरी पर स्थित जीवाएँ एक-दूसरे की होती हैं
(क) दुगुनी
(ख) तिगुनी
(ग) आधी
(घ) बराबर
उत्तर:
(घ) बराबर
प्रश्न 6.
एक वृत्त के किसी चाप का डिग्रीमाप 180° है, वह चाप है
(क) दीर्घ चाप
(ख) लघु चाप
(ग) वृत्त
(घ) अर्द्धवृत्त
उत्तर:
(घ) अर्द्धवृत्त
प्रश्न 7.
तीन संरेखीय बिन्दुओं से गुजरने वाले वृत्तों (RBSESolutions.com) की संख्या है
(क) एक
(ख) दो।
(ग) शून्य
(घ) अनन्त
उत्तर:
(क) एक
प्रश्न 8.
यदि किसी वृत्त में चाप AB = चाप BA हों, तो चाप है|
(क) दीर्घ चाप
(ख) लघु चाप
(ग) अर्द्ध वृत्त
(घ) वृत्त
उत्तर:
(ग) अर्द्ध वृत्त
प्रश्न 9.
यदि वृत्त का व्यास दो जीवाओं में से प्रत्येक को समद्विभाजित करे तो जीवाएँ होंगी
(क) समान्तर
(ख) लम्बवत्
(ग) प्रतिच्छेदी
(घ) उपरोक्त में से कोई नहीं
उत्तर:
(क) समान्तर
प्रश्न 10.
यदि सर्वांगसम वृत्तों में दो चाप बराबर हों, तो उनकी (RBSESolutions.com) संगत जीवाएँ होंगी
(क) समान्तर
(ख) समान
(ग) लम्बवत्
(घ) प्रतिच्छेदी
उत्तर:
(ख) समान
![]()
प्रश्न 11.
किसी वृत्त का AD एक व्यास है और AB एक जीवा है। यदि AD = 34 सेमी., AB = 30 सेमी. हैं, तो वृत्ते के केन्द्र से AB की दूरी है
(क) 17 सेमी.
(ख) 15 सेमी.
(ग) 4 सेमी.
(घ) 8 सेमी.
उत्तर:
(घ) 8 सेमी.
प्रश्न 12.
आकृति में, यदि OA = 5 सेमी., AB = 8 सेमी. तथा OD जीवा AB पर लम्ब है, तो CD बराबर है
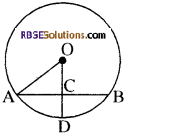
(क) 2 सेमी.
(ख) 3 सेमी.
(ग) 4 सेमी.
(घ) 5 सेमी.
उत्तर:
(क) 2 सेमी.
प्रश्न 13.
यदि AB = 12 सेमी., BC = 16 सेमी. और AB रेखाखण्ड BC पर लम्ब है, तो A, B और C से होकर (RBSESolutions.com) जाने वाले वृत्त की त्रिज्या है
(क) 6 सेमी.
(ख) 8 सेमी.
(ग) 10 सेमी.
(घ) 12 सेमी.
उत्तर:
(ग) 10 सेमी.
प्रश्न 14.
आकृति में, यदि ∠ABC = 20° है, तो। ∠AOC बराबर है
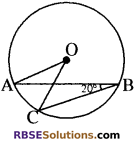
(क) 20°
(ख) 40°
(ग) 60°
(घ) 10°
उत्तर:
(ख) 40°
प्रश्न 15.
आकृति में, यदि AOB वृत्त का एक व्यास (RBSESolutions.com) तथा AB = BC है, तो ∠CAB बराबर है
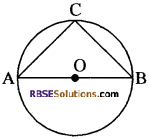
(क) 30°
(ख) 60°
(ग) 90°
(घ) 45°
उत्तर:
(घ) 45°
![]()
प्रश्न 16.
आकृति में, यदि ∠OAB = 40° है, तो ∠ACB बराबर है
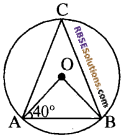
(क) 50°
(ख) 40°
(ग) 60°
(घ) 70°
उत्तर:
(क) 50°
प्रश्न 17.
आकृति में, यदि ∠DAB = 60°, ∠ABD = 50° है, तो ∠ACB बराबर है
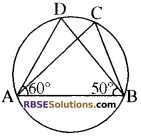
(क) 60°
(ख) 50°
(ग) 70°
(घ) 80°
उत्तर:
(ग) 70°
प्रश्न 18.
चतुर्भुज की एक भुजा AB उसके परिगत वृत्त का एक व्यास (RBSESolutions.com) है तथा ∠ADC = 140° है। तब, ∠BAC बराबर है
(क) 80°
(ख) 50°
(ग) 40°
(घ) 30°
उत्तर:
(ख) 50°
प्रश्न 19.
आकृति में, BC वृत्त का व्यास है तथा ∠BA0 = 60° है। तब, ∠ADC बराबर
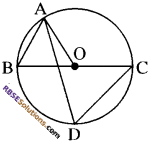
(क) 30°
(ख) 45°
(ग) 60°
(घ) 120°
उत्तर:
(ग) 60°
प्रश्न 20.
आकृति में, ∠AOB = 90° और ∠ABC = 30° है। (RBSESolutions.com) तब, ∠CAO बराबर है
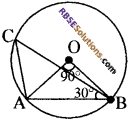
(क) 30°
(ख) 45°
(ग) 90°
(घ) 60°
उत्तर:
(घ) 60°
![]()
प्रश्न 21.
यदि एक वृत्त की दो बराबर जीवाएँ परस्पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के दो भाग दूसरी जीवा के दोनों भागों के पृथक्पृथक् बराबर होते हैं।
हल:
दिया है-
AB व CD दो बराबर जीवाएँ, जो कि P बिन्दु पर काटती हैं। (RBSESolutions.com) सिद्ध करना है–
AP = CP
BP = DP
रचना-
OP को जोड़ते हैं एवं
OL ⊥ AB
OM ⊥ CD खींचते हैं।
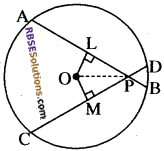
उपपत्ति-
∵ OL ⊥ AB और OM ⊥ CD
∴ L एवं M, AB व CD के मध्य बिन्दु हैं।
समान जीवाएँ केन्द्र से समान दूरी पर स्थित होती हैं।

प्रश्न 22.
यदि P, Q और R क्रमशः एक त्रिभुज की BC, CA और AB भुजाओं के मध्य-बिन्दु हैं (RBSESolutions.com) तथा AD शीर्ष A से BC पर लम्ब है, तो सिद्ध कीजिए कि बिन्दु P, Q, R और D चक्रीय हैं।
हल:
दिया है-P, Q, R क्रमशः BC, CA एवं AB भुजाओं के मध्य बिन्दु हैं तथा AD शीर्ष A से BC पर लम्बे हैं।
सिद्ध करना है-
P, Q, R एवं D चक्रीय है।
रचना-
RD, QD, PR एवं PQ को जोड़ा।
उपपत्ति-
RP, R व P को जोड़ती है, जो कि AB व BC को मध्य बिन्दु है
∴ RP || AC (मध्य बिन्दु प्रमेय)। इसी प्रकार, PQ || AB
∴ ARPQ एक समान्तर चतुर्भुज है।
∴ ∠RAQ = ∠RPQ …..(1) (विपरीत कोण)
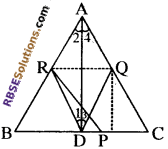
∆ABD एक समकोण त्रिभुज है एवं DR एक माध्यिका है।

प्रश्न 23.
∆BCD एक समान्तर चतुर्भुज है। A और B से होकर एक वृत्त इस प्रकार खींचा जाता (RBSESolutions.com) है कि वह AD को P पर और BC को Q पर प्रतिच्छेद करता है। सिद्ध कीजिए कि P, Q, C और D चक्रीय हैं।
हल:
∆BCD एक समान्तर चतुर्भुज है। वृत्त खींचा जो AD को P एवं BC को BP Q पर काटता है।
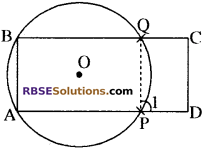
PQ को जोड़ते हैं।
∆PQB एक चक्रीय चतुर्भुज की A भुजा AP को D तक बढ़ाया।
∴ बहिष्कोण ∠1 = आन्तरिक कोण ∠B
∴ BA || CD एवं BC उसको काटता है।
∠B +∠C = 180°
∠1 +∠C = 180° [समीकरण (1) से]
∴ PDCQ एक चक्रीय चतुर्भुज है।
अतः P, Q, C एवं D चक्रीय है।
प्रश्न 24.
सिद्ध कीजिए कि एक त्रिभुज के किसी कोण का समद्विभाजक और (RBSESolutions.com) उसकी सम्मुख भुजा का लम्ब समद्विभाजक, यदि प्रतिच्छेद करते हैं, तो उस त्रिभुज के परिवृत्त पर प्रतिच्छेद करते हैं।
हल:
दिया है-
∆ABC के आधार BC का लम्ब समद्विभाजक XY है। ABDC, ∆ABC का परिवृत्त है। लम्ब समद्विभाजक XY परिवृत्त को D पर काटता है। XY, BC को M पर काटता है।
सिद्ध करना है-
∠A को समद्विभाजक भी बिन्दु D से होकर जाता है।
रचना-
DB तथा DC को मिलाया।
उपपत्ति-
∵ XY, BC को लम्ब समद्विभाजक है और यह परिवृत्त को बिन्दु D पर काटता है।
∴ बिन्दु D, परिवृत्त पर भी है और XY पर भी।
समकोण ∆BDM और ∆CDM में
BM = CM (XY, BC का लम्ब समद्विभाजक है)
MD = MD (उभयनिष्ठ भुजा है)
∠BMD = ∠CMD (∵ XY ⊥ BC)
भुजा-कोण-भुजा सर्वांगसमता के (RBSESolutions.com) गुणधर्म से,
∆BDM = ∆CDM
BD = CD
∵ बिन्दु D, परिवृत्त पर भी स्थित है।
∴ परिवृत्त में, जीवा BD = जीवा CD
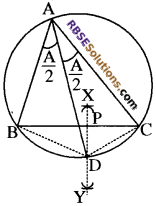
∴ चाप BD = चाप CD (सर्वांगसम त्रिभुजों की संगत भुजाएँ) किसी वृत्त की समान जीवाएँ समान चाप काटती हैं।
∴ चाप BD द्वारा बिन्दु A पर अन्तरित कोण = चाप CD द्वारा बिन्दु A पर अन्तरित कोण
∠BAD = ∠CAD
∴ AD, ∠A का समद्विभाजक है।
अतः ∠A का समद्विभाजक AD भी बिन्दु D से होकर जाता है। (इतिसिद्धम् )
![]()
प्रश्न 25.
यदि किसी वृत्त AYD∠BWCX की दो जीवाएँ AB और CD समकोण पर प्रतिच्छेद (RBSESolutions.com) करती। हैं (आकृति देखिए), तो सिद्ध कीजिएं कि चाप CXA + चाप D∠B = चाप AYD + चाप BWC = एक अर्धवृत्त है।
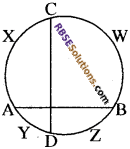
हल:
दिया है-
किसी वृत्त की दो जीवाएँ AB व At CD समकोण पर प्रतिच्छेद करती हैं।
सिद्ध करना है-
चाप CXA + चाप D∠B
= चाप AYD + चाप BWC
= एक अर्द्धवृत्त
रचना-
A को C, D एवं C को B से। मिलाते हैं।
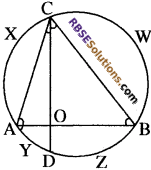
उपपत्ति-
दो जीवाएँ AB वे CD समकोण पर बिन्दु O पर (RBSESolutions.com) काटती हैं। ∆AOD में-
∠DAO + ∠ODA + ∠AOD = 180°
∠DA0 + ∠ODA + 90° = 180°
∠DAO + ∠ODA = 90°
चाप \(\widehat{D Z B}\) एवं चाप \(\widehat{C X A}\) द्वारा क्रमश: ∠DAO एवं ∠ODA बनाते हैं।
∴ चाप \(\widehat{D Z B}\) + चाप \(\widehat{C X A}\) = 90° …..(1)
अब ADOB में-
∠BDO + ∠OBD + ∠DOB = 180°
∠BDO +∠OBD + 90° = 180°
∠BDO + ∠OBD = 90°
पुनः चाप \(\widehat{B W A}\) एवं चाप \(\widehat{A Y D}\) द्वारा क्रमशः ∠BDO एवं ∠OBD बनाते हैं।
∴ चाप \(\widehat{A Y D}\) + चाप AYD = 90° …..(2)
समीकरण (1) व (2) से,
चाप \(\widehat{D Z B}\) + चाप \(\widehat{C X B}\) = चाप \(\widehat{B W C}\) + चाप \(\widehat{A Y D}\) = 90°
हम जानते हैं कि किसी वृत्त का चाप, किसी बिन्दु पर समकोण बनाता है जो कि एक अर्द्धवृत्त के वृत्तखण्ड में वैकल्पिक होता है।
अतः चाप \(\widehat{C X A}\) + चाप \(\widehat{D Z B}\) = चाप \(\widehat{A Y D}\) + चाप \(\widehat{B W C}\) = अर्द्धवृत्त
प्रश्न 26.
यदि ABC किसी वृत्त के अन्तर्गत एक समबाहु त्रिभुज है तथा P लघु चाप BC पर स्थित कोई बिन्दु है, (RBSESolutions.com) जो B या C के सम्पाती नहीं है, तो सिद्ध कीजिए कि PA कोण BPC का समद्विभाजक है।
हल:
दिया है-
ABC किसी वृत्त के अन्तर्गत एक समबाहु त्रिभुज है तथा P लघुचाप BC पर स्थित कोई बिन्दु है जो B या C के सम्पाती नहीं है।
सिद्ध करना है-
PA, कोण BPC का समद्विभाजक है। A
उपपत्ति-
वृत्त की समान जीवाएँ, वृत्त के केन्द्र पर समान कोण अन्तरित करती हैं।
∴ जीवा AB = जीवा AC
∠AOB = ∠AOC …..(1)
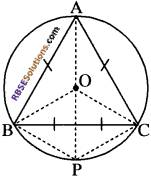
एक चाप द्वारा वृत्त के केन्द्र पर अन्तरित कोण, वृत्त के शेष भाग के किसी बिन्दु पर (RBSESolutions.com) अन्तरित कोण का दोगुना होता है।
∴ ∠APC = \(\frac{1}{2}\) ∠AOC …..(2)
एवं ∠APB = \(\frac{1}{2}\) ∠AOC …..(3)
समीकरण (2) तथा (3) को बराबर करने पर
∴ ∠APC = ∠APB.
अतः PA, कोण BPC को समद्विभाजक है। इतिसिद्धम्
प्रश्न 27.
आकृति में, AB और CD एक वृत्त की दो जीवाएँ हैं, जो E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∠AEC = \(\frac{1}{2}\) (चाप CXA द्वारा केन्द्र पर अन्तरित कोण + चाप DYB द्वारा केन्द्र पर अन्तरित कोण) है।
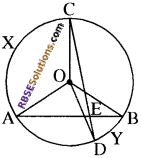
हल:
दिया है-
AB एवं CD एक वृत्त की दो जीवाएँ हैं, जो E पर प्रतिच्छेद करती हैं।
सिद्ध करना है-
∠AEC = \(\frac{1}{2}\) (चाप CXA द्वारा केन्द्र पर अन्तरित कोण + चाप DYB द्वारा केन्द्र पर अन्तरित कोण)
रचना-
AC, BC एवं BD को मिलाते हैं।
उपपत्ति-
AB एवं CD वृत्त की दो जीवाएँ हैं। जो E पर प्रतिच्छेद करती हैं।
हम जानते हैं कि एक चाप द्वारा वृत्त के केन्द्र पर अन्तरित कोण, वृत्त के शेष भाग (RBSESolutions.com) के किसी बिन्दु पर अन्तरित कोण का दोगुना होता है।
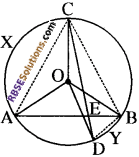
चाप CXA, केन्द्र पर ∠AOC एवं शेष भाग पर ∠ABC अन्तरित करता है।
∠AOC = 2∠ABC …..(1)
इसी प्रकार, ∠BOD = 2∠BCD ………….(2)
समीकरण (1) व (2) को जोड़ने पर,
∠AOC + ∠BOD = 2(∠ABC + ∠BCD) ………….(3)
त्रिभुज का बहिण, आन्तरिक विपरीत कोणों के योग के बराबर होता है। इसलिए त्रिभुज CEB में,
∠AEC = ∠ABC + ∠BCD . …..(4)
समीकरण (3) व (4) से,
∠AOC + ∠BOD = 2∠AEC
= ∠AEC = \(\frac{1}{2}\) (∠AOC + ∠BOD)
अतः ∠AEC = \(\frac{1}{2}\) (चाप CXA द्वारा केन्द्र पर आन्तरिक कोण + चाप DYB द्वारा केन्द्र पर अन्तरित कोण)
![]()
प्रश्न 28.
यदि एक चक्रीय चतुर्भुज ABCD के सम्मुख कोणों के समद्विभाजक इस चतुर्भुज के (RBSESolutions.com) परिगत वृत्त को P और Q बिन्दुओं पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि PQ इस वृत्त का व्यास है।
हल:
दिया है-
एक चक्रीय चतुर्भुज ABCD के सम्मुख कोणों के समद्विभाजक इस चतुर्भुज के परिगत वृत्त को P और Q बिन्दुओं पर प्रतिच्छेद करते हैं।
सिद्ध करना है-
PQ वृत्त का व्यास है।
रचना-
AP, QC, QD एवं AQ को। मिलाते हैं।
उपपत्ति-
PQ वृत्त का व्यास होने के लिए हमें सिद्ध करना होगा
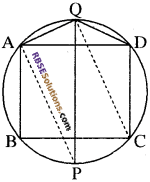
∠PAQ = 90°
ABCD एक चक्रीय चतुर्भुज है
∠A+∠C = 180°
\(\frac{1}{2}\) ∠A + \(\frac{1}{2}\) ∠C = 90°
∠PAD + ∠QCD = 90° ………..(1)
लेकिन कोण QCD और कोण QAD, जीवा QD के वृत्त के समान (RBSESolutions.com) वृत्तखण्ड के कोण हैं।
∴ ∠QCD = ∠QAD …..(2)
समीकरण (1) व (2) से,
∠PAD + ∠QAD = 90°
∠PAQ = 90°
∠PAQ, एक अर्द्धवृत्त में स्थित है।
अतः PQ इस वृत्त का व्यास है।
प्रश्न 29.
एक वृत्त की त्रिज्या 2 cm. है। 2 cm. लम्बाई वाली जीवा द्वारा यह वृत्त दो वृत्त-खण्डों में विभाजित किया जाता है। सिद्ध कीजिए कि इस जीवा द्वारा दीर्घ वृत्त-खण्ड के किसी बिन्दु पर बना कोण 45° है।
हल:
दिया है:
वृत्त की त्रिज्या = 2 सेमी. तथा 2 सेमी. वाली जीवा द्वारा (RBSESolutions.com) इस वृत्त को दो वृत्त खण्डों में विभाजित किया जाता है।
सिद्ध करना है-
2 सेमी. वाली जीवा द्वारा दीर्घ वृत्त-खण्ड के किसी बिन्दु पर ना कोण 45° है।
अर्थात् ∠BAC = 45°

∴ ∠BOC = 90° (पाइथागोरस प्रमेय के विलोम द्वारा)
अब चाप BC वृत्त के केन्द्र 0 पर ∠BOC तथा शेष भाग पर ∠BAC अन्तरित करता है।
\(\begin{array}{ll}{\therefore \quad \angle B A C=\frac{1}{2} \angle B O C=\frac{1}{2} \times 90^{\circ}=45^{\circ}} \\ {\Rightarrow \quad \angle B A C=45^{\circ}}\end{array}\)
प्रश्न 30.
AB और AC त्रिज्या r वाले एक वृत्त की दो जीवाएँ इस (RBSESolutions.com) प्रकार हैं कि AB = 2AC है। यदि p और q क्रमशः केन्द्र से AB और AC की दूरियाँ हैं, तो सिद्ध कीजिए कि \(4 q^{2}=p^{2}+3 r^{2}\) है।
हल:
दिया है-
AB और AC त्रिज्या r वाले वृत्त की जीवाएँ हैं ताकि AB = 2AC.

समकोण ∆AOL में,

समीकरण (1) तथा (2) को बराबर करने पर
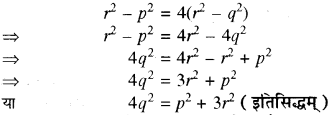
![]()
प्रश्न 31.
आकृति में, O वृत्त का केन्द्र है। (RBSESolutions.com) और ∠BCO = 30° है।r और y ज्ञात कीजिए।
हल:

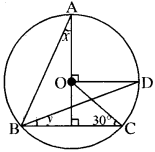
हम जानते हैं कि एक चाप द्वारा वृत्त के केन्द्र मे 4 पर अन्तरित कोण वृत्त के शेष भाग के किसी बिन्दु पर अन्तरित कोण का दोगुना होता है।
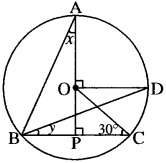
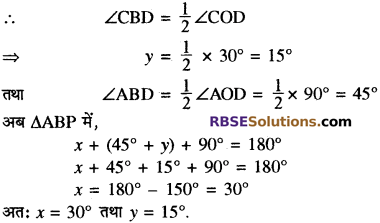
प्रश्न 32.
आकृति में, O वृत्त का केन्द्र है। BD = OD और CD ⊥ AB है। (RBSESolutions.com) ∠CAB ज्ञात कीजिए।
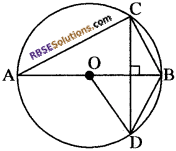
हल:
दिया है-
BD = OD
CD ⊥ AB
ज्ञात करना है-
∠CAB. AODB में,
BD = OD (दिया है)
∠DOB = ∠DBO (त्रिभुज के समान भुजाओं के विपरीत कोण समान होते हैं।)
∆ODP एवं ∆BDP में,
∠DOP = ∠DBP (∵ 2DOB = ∠DBO)
∠DPO = ∠DPB (प्रत्येक 90°)
OD = BD (दिया है)।
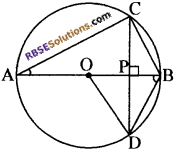
∴ ∆ODP = ∆BDP (AAS नियम से)
⇒ ∠ODP = ∠BDP …..(1) (CPCT)
पुन: OD = OB (समान वृत्त की त्रिज्याएँ)
लेकिन OD = BD
⇒ OB = OD = BD, ∴ ∆OBD एक समबाहु त्रिभुज है।
∴ ∠ODB = 60° =
\(\Rightarrow \quad \angle \mathrm{BDP}=\frac{1}{2} \angle \mathrm{ODB}\) [समीकरण (1) से)
\(\Rightarrow \quad \angle B D P=\frac{1}{2} \times 60^{\circ}=30^{\circ}\)
या ∠CDB = 30°
वृत्त के समान वृत्तखण्ड में कोण समान होते हैं अतः
∠CAB = ∠CDB = 30°.
प्रश्न 33.
सिद्ध कीजिए कि वृत्त के अन्दर किसी बिन्दु से होकर जाने वाली सभी (RBSESolutions.com) जीवाओं में से वह जीवा सबसे छोटी होती है, जो उस बिन्दु से होकर जाने वाले व्यास पर लम्ब होती है।
हल:
माना AB व CD वृत्त की दो जीवाएँ हैं।
OL ⊥ AB, OM ⊥ CD.
ताकि OL ∠ OM.
OA व OC को मिलाया।
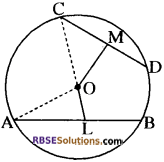
वृत्त के केन्द्र से जीवा पर डाले गये लम्ब , इसको समद्विभाजित करता है।
∴ AL = \(\frac{1}{2}\) AB तथा CM = \(\frac{1}{2}\) CD.
∆OAL तथा ∆OCM में
\(\mathrm{OA}^{2}=\mathrm{OL}^{2}+\mathrm{AL}^{2}\) तथा \(\mathrm{OC}^{2}=\mathrm{OM}^{2}+\mathrm{CM}^{2}\)

अतः वृत्त के अन्दर किसी बिन्दु से होकर जाने वाली सभी जीवाओं (RBSESolutions.com) में से वह जीवा सबसे छोटी होती है, जो उस बिन्दु से होकर जाने वाले व्यास पर लम्ब होती है। (इतिसिद्धम्)
![]()
अन्य महत्त्वपूर्ण प्रश्न
वस्तुनिष्ठ प्रश्न
प्रश्न 1.
वृत्त C (O, 13) की एक जीवा की केन्द्र से दूरी 5 सेमी. है, जीवा की लम्बाई है 15 सेमी.
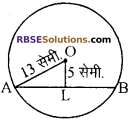
(क) 24 सेमी.
(ख) 20 सेमी.
(ग) 16 सेमी.
(घ) 12 सेमी.
उत्तर:
(क) 24 सेमी.
प्रश्न 2.
वृत्त C (O, 5) की जीवा AB = 8 सेमी. है, (RBSESolutions.com) जीवा AB की 0 से दूरी है
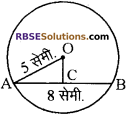
(क) 5 सेमी.
(ख) 4 सेमी.
(ग) 3 सेमी.
(घ) 1 सेमी.
उत्तर:
(ग) 3 सेमी.
प्रश्न 3.
AB और CD वृत्त C (0, r) के व्यास हैं। 8 सेमी. जहां AC || DB और DA || BC यदि ∠OBD = 50° हो तो ∠ AOC का मान।
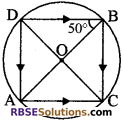
(क) 50°
(ख) 60°
(ग) 70°
(घ) 80°
उत्तर:
(घ) 80°
प्रश्न 4.
यदि किसी वृत्त में m(AB) = m(BA) है तो वह चाप है
(क) दीर्घ चाप
(ख) लघु चाप
(ग) अर्ध वृत्त
(घ) वृत्त
उत्तर:
(ग) अर्ध वृत्त
प्रश्न 5.
वृत्त C (0, 3) तथा C (0, 3) में जीवा AB = जीवा CD है। (RBSESolutions.com) यदि \(\mathrm{m}(\widehat{\mathrm{AB}})=\mathrm{m}(\widehat{\mathrm{BA}})\) हो तो का मान है
(क) 70°
(ख) 140°
(ग) 210°
(घ) 290°
उत्तर:
(घ) 290°
प्रश्न 6.
वृत्त में 24 सेमी. लम्बाई की एक जीवा केन्द्र से 5 सेमी. दूरी पर है। वृत्त का व्यास होगा
(क) 20 सेमी.
(ख) 13 सेमी.
(ग) 26 सेमी.
(घ) 50 सेमी.
उत्तर:
(ग) 26 सेमी.
प्रश्न 7.
दी गई आकृति में AB तथा CD दो जीवाएँ वृत्त के केन्द्र O से 4 सेमी. की दूरी पर हैं। (RBSESolutions.com) यदि OA = 5 सेमी. है, तो जीवा CD की लम्बाई है
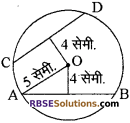
(क) 3 सेमी.
(ख) 4 सेमी.
(ग) 5 सेमी.
(घ) 6 सेमी.
उत्तर:
(घ) 6 सेमी.
![]()
प्रश्न 8.
बराबर वृत्तों में बराबर चापों द्वारा केन्द्रों पर अन्तरित कोण होते हैं
(क) बराबर
(ख) आधा
(ग) दुगुना
(घ) चौगुना
उत्तर:
(क) बराबर
प्रश्न 9.
एक ही वृत्त में बराबर जीवाओं द्वारा काटे गए चाप होते हैं
(क) आधा
(ख) बराबर
(ग) दुगुना
(घ) तिगुना
उत्तर:
(ख) बराबर
प्रश्न 10.
एक वृत्त की दो जीवाएँ AB और CD परस्पर बराबर व समान्तर हैं। (RBSESolutions.com) यदि वृत्त की त्रिज्या 5 सेमी. तथा जीवा की लम्बाई 6 सेमी. है तो दोनों जीवाओं के मध्य की दूरी होगी
(क) 5 सेमी.
(ख) 6 सेमी.
(ग) 8 सेमी.
(घ) 10 सेमी.
उत्तर:
(ग) 8 सेमी.
प्रश्न 11.
आकृति में ABCDE अर्द्धवृत्त में। बना पंचभुज है, तो ∠ABC + ∠CDE का मान है
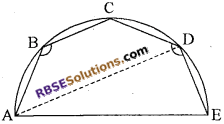
(क) 180°
(ख) 216°
(ग) 270°
(घ) 240°
उत्तर:
(ग) 270°
प्रश्न 12.
दी गई आकृति में, AB वृत्त का व्यास है तथा ∠PAB = 50° हो तो ∠PCA का मान है
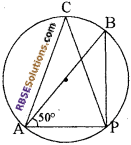
(क) 40°
(ख) 90°
(ग) 50°
(घ) 60°
उत्तर:
(क) 40°
प्रश्न 13.
दी गई आकृति में 0 वृत्त का केन्द्र है। (RBSESolutions.com) यदि ∠OAB = 30° तथा ∠OBC = 40° हो तो ∠AOC का मान है
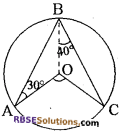
(क) 70°
(ख) 130°
(ग) 140°
(घ) 150°
उत्तर:
(ग) 140°
![]()
प्रश्न 14.
दी गई आकृति में 0 वृत्त का केन्द्र है। यदि ∠OAB = 25° तथा ∠OCB = 35° हैं, तो ∠AOC का माप है
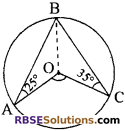
(क) 50°
(ख) 70°
(ग) 100°
(घ) 120°
उत्तर:
(घ) 120°
प्रश्न 15.
दी गई आकृति में 0 वृत्त का केन्द्र है। यदि ∠AOB = 100° है, तो कोण 8 का मान है
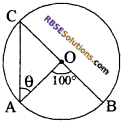
(क) 40°
(ख) 50°
(ग) 60°
(घ) 90°
उत्तर:
(ख) 50°
प्रश्न 16.
दिये गये चित्र में, AB वृत्त का व्यास है। (RBSESolutions.com) यदि ∠BCD = 128° हो, तो ∠ABD का मान है
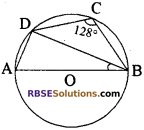
(क) 26°
(ख) 38°
(ग) 52°
(घ) 64°
उत्तर:
(ख) 38°
प्रश्न 17.
दिये गये चित्र में, 0 वृत्त का केन्द्र है। यदि ∠MKN = 33° एवं ∠MNK = 47° है तो × का मान है
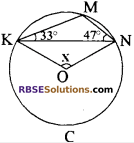
(क) 80°
(ख) 100°
(ग) 160°
(घ) 200°
उत्तर:
(ग) 160°
प्रश्न 18.
दिये गये चित्र में, 0 वृत्त का केन्द्र है। (RBSESolutions.com) यदि ∠AOD = 70° हो, तो ∠OAC है
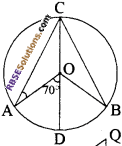
(क) 20°
(ख) 35°
(ग) 55°
(घ) 70°
उत्तर:
(ख) 35°
प्रश्न 19.
दिये गये चित्र में, AB वृत्त का व्यास है। यदि ∠PBQ = 30° है, तो ∠PQB का मान है
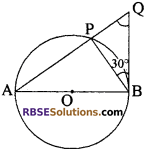
(क) 30°
(ख) 40°
(ग) 50°
(घ) 60°
उत्तर:
(घ) 60°
![]()
प्रश्न 20.
दिये गये चित्र में, ‘O’ वृत्त का केन्द्र है। (RBSESolutions.com) यदि ∠APB = 40° है, तो ∠AQB का मान है
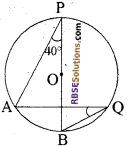
(क) 60°
(ख) 50°
(ग) 40°
(घ) 30°
उत्तर:
(ग) 40°
प्रश्न 21.
दिये गये चित्र में, AD वृत्त का व्यास है। यदि ∠ADB = 30° है तथा ∠BCD = 8 तो 6 का मान है
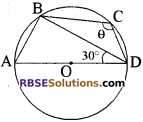
(क) 150°
(ख) 130°
(ग) 120°
(घ) 90°
उत्तर:
(ग) 120°
प्रश्न 22.
दिये गये चित्र में ∠ABO = 35°, ∠CDE = x° तथा DE वृत्त की स्पर्श रेखा है। x का मान होगा
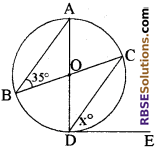
(क) 35°
(ख) 55°
(ग) 70°
(घ) 90°
उत्तर:
(ख) 55°
प्रश्न 23.
चित्र में ABCD एक चक्रीय चतुर्भुज है। (RBSESolutions.com) यदि ∠ADNC = 68° हो तो ∠ABC का मान
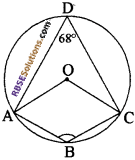
(क) 68°
(ख) 44°
(ग) 112°
(घ) 90°
उत्तर:
(ग) 112°
प्रश्न 24.
चित्र में, O केन्द्र वाले एक वृत्त में AB व्यास तथा BD एक जीवा है। जीवा BD वृत्त के किसी बिन्दु C पर 112° कोण अन्तरित करती है, तो ∠ABD का मान है
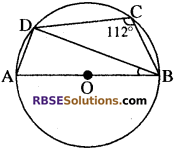
(क) 56°
(ख) 68°
(ग) 22°
(घ) 34°
उत्तर:
(ग) 22°
प्रश्न 25.
चित्र में व्यास EC जीवा AD के समान्तर (RBSESolutions.com) एवं ∠ABC = 50° हो, तो ∠CAD का मान
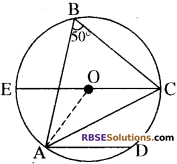
(क) 50°
(ख) 40°
(ग) 130°
(घ) 25°
उत्तर:
(ख) 40°
![]()
अतिलघूत्तरात्मक प्रश्न
प्रश्न 1.
एक वृत्त की त्रिज्या 4 सेमी. है। इस वृत्त में दो समान्तर जीवाओं के मध्य बिन्दुओं से गुजरने वाली जीवा की लम्बाई लिखिये ।।
हल:
समान्तर जीवाओं का मध्य बिन्दु केन्द्र से जाता है। अतः वृत्त का व्यास इसकी जीवा होगी।
जीवा की लम्बाई = 2 × त्रिज्या = 2 × 4 = 8 सेमी.
प्रश्न 2.
दी गई आकृति में O वृत्त का केन्द्र है। (RBSESolutions.com) तथा जीवाएँ AB = BC हैं। यदि ∠BOC = 100° है, तो ∠AOB का मान लिखिए।
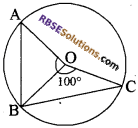
उत्तर:
∠AOB = 100°
प्रश्न 3.
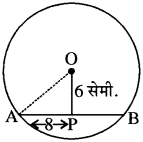
यदि 16 सेमी. लम्बाई की एक जीवा वृत्त के केन्द्र से 6 सेमी. की दूरी पर है, तो उस वृत्त के व्यास की लम्बाई लिखिए।
हल:
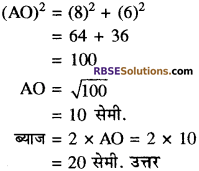
प्रश्न 4.
वृत्त C (0, 5) तथा C (0′, 5) में जीवा AB = जीवा CD है। (RBSESolutions.com) यदि \(\mathrm{m}(\overline{\mathrm{AB}})=60^{\circ}\) है, तो \(\mathrm{m}(\overline{\mathrm{CD}})\) का मान लिखिए।
हल:
\(\mathrm{m}(\overline{\mathrm{CD}})=60^{\circ}\)
प्रश्न 5.
एक वृत्त की दो जीवाएँ AB तथा CD हैं जो परस्पर समान्तर और बराबर हैं। यदि प्रत्येक की लम्बाई 8 सेमी. हो और वृत्ते की त्रिज्या 5 सेमी. हो तो उनके बीच की दूरी लिखो।
हल:
केन्द्र से AB की दूरी \(=\sqrt{5^{2}-4^{2}}=\sqrt{9}=3\) सेमी. अत: दोनों के मध्य की दूरी = 3 × 2 = 6 सेमी.
प्रश्न 6.
एक वृत्त की त्रिज्या 5 सेमी. और वृत्त के केन्द्र से एक जीवा पर लम्ब की लम्बाई 4 सेमी. है तो जीवा की लम्बाई ज्ञात करो।
हल:
\(2 \sqrt{5^{2}-4^{2}}=2 \times 3=6\) सेमी.
![]()
प्रश्न 7.
एक वृत्त की जीवा 7 सेंमी. है और केन्द्र से जीवा की दूरी 1.2 सेमी. है तो वृत्त की त्रिज्या ज्ञात करो।
हल:
त्रिज्या
\(\begin{array}{l}{=\sqrt{(3.5)^{2}+(1.2)^{2}}} \\ {=\sqrt{12.25+1.44}=\sqrt{13.69}=3.7}\end{array}\) सेमी.
प्रश्न 8.
एक वृत्त 5 सेमी. त्रिज्या का है, इसकी सबसे बड़ी (RBSESolutions.com) जीवा की लम्बाई बताइए।
उत्तर:
वृत्त की सबसे बड़ी जीवा व्यास होती है।
अतः व्यास की लम्बाई = 2 × 5 = 10 सेमी.
प्रश्न 9.
यदि 16 सेमी. लम्बाई की एक जीवा वृत्त के केन्द्र से 6 सेमी. की। दूरी पर है, तो उस वृत्त की त्रिज्या लिखिए।
हल:
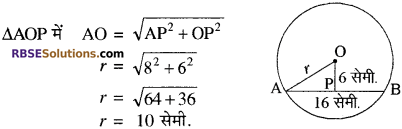
प्रश्न 10.
8 सेमी. लम्बाई की एक जीवा वृत्त के केन्द्र से 3 सेमी. की दूरी पर है, (RBSESolutions.com) तो उस वृत्त की त्रिज्या लिखिए।
हल:
वृत्त की त्रिज्या OA = ?

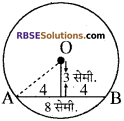
अतः वृत्त की त्रिज्या = 5 सेमी.
प्रश्न 11.
वृत्त में किन्हीं दो त्रिज्याओं और उनके अन्तिम बिन्दुओं से बनने वाले चाप (RBSESolutions.com) से घिरे क्षेत्र का नाम लिखिए।
हल:
त्रिज्यखण्ड।
प्रश्न 12.
दी गई आकृति में, AOB वृत्त का व्यास है तथा ∠ROS = 42° है, तो ∠RTS की माप ज्ञात कीजिये।
हल:
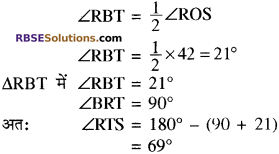
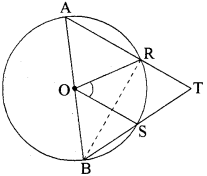
![]()
प्रश्न 13.
दी गई आकृति में AB वृत्त का व्यास है। (RBSESolutions.com) यदि ∠ABC = 59° है तो ∠BAC का मान लिखिए।
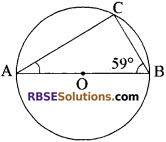
हल:
∠BAC = 90° – 59° = 31°
क्योंकि ∠ACB = 90° है।
प्रश्न 14.
दी गई आकृति में O वृत्त का केन्द्र है। यदि ∠BAC = 30° है, तो ∠ABC का मान लिखिए।
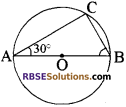
हल:
∠ABC = 180° – (∠BAC + ∠ACB).
= 180° – (30° + 90°)
= 60°
प्रश्न 15.
दिये गये चित्र में ‘O’ वृत्त का केन्द्र है। ∆BCD एक चक्रीय चतुर्भुज है। ∠PCB = 70° है, तो ∠BOD का (RBSESolutions.com) मान लिखिये।
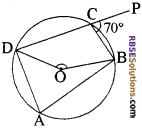
हल:
∠BAD = ∠BCP = 70°
तथा ∠BOD = 2 ∠BAD
= 2 × 70 = 140°
प्रश्न 16.
दिये गये चित्र में ∠x व ∠y का मान ज्ञात करो।
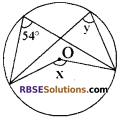
हल:
∠x = 2 × 54 = 1080
तथा ∠x = ∠y अतः
y = \(\frac{108}{2}\) = 54°
प्रश्न 17.
चित्र में चाप BD और चाप CD द्वारा केन्द्र पर अन्तरित (RBSESolutions.com) कोण 80° और 60° है, तो ∠BAC ज्ञात कीजिए।
हल:
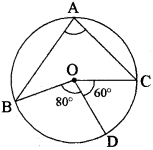
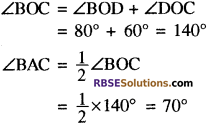
प्रश्न 18.
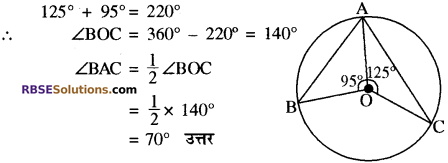
चित्र में O केन्द्र वाले एक वृत्त में चाप BC द्वारा केन्द्र O पर ∠BOC तथा शेष परिधि के किसी बिन्दु A पर ∠BAC अन्तरित होता है। यदि ∠AOB = 95° तथा ∠AOC = 125° तो ∠BAC का मान ज्ञात कीजिए।
हल:
![]()
प्रश्न 19.
चित्र में चाप AB द्वारा वृत्त के केन्द्र 0 पर (RBSESolutions.com) अन्तरित कोण 120° है तथा AC वृत्त का व्यास है, तो ∠OBC का मान लिखिए।
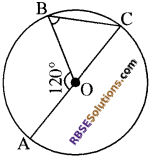
हल:
∠COB = 180° – 120° = 60°
OC = OB एक ही वृत्त की त्रिज्यायें हैं।
∴ ∠C =∠B अतः ∠OBC = 60°
प्रश्न 20.
चित्र में O केन्द्र वाले एक ही वृत्त में ∆BCD एक चक्रीय चतुर्भुज है। यदि बहिष्कोण ∠CBE = 65° तो ∠AOC का मान ज्ञात कीजिए।
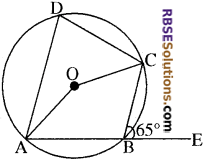
हल:
∠CBE = ∠ADC
∴ ∠ADC = 65°
∴ AOC = 2∠ADCAS
= 2 × 65° = 130°
प्रश्न 21.
एक वृत्त के उस चाप का नाप लिखिए जो वृत्त के शेष (RBSESolutions.com) भाग पर समकोण बनाता है।
हल:
एक वृत्त का वह चाप जो वृत्त के शेष भाग पर समकोण अन्तरित करता है, एक अर्द्धवृत्त होता है।
प्रश्न 22.
r त्रिज्या वाले वृत्त के केन्द्र पर 180° कोण अन्तरित करने वाले चाप की लम्बाई लिखिए।
हल:
πr
प्रश्न 23.
चित्र में यदि ∠ADC = 80° हो, तो ∠CBE का मान लिखिए।
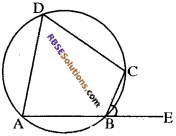
हल:
अन्तरित बहिष्कोण अन्तराभिमुख कोण के बराबर होता है।
∴ ∠CBE = 80°
प्रश्न 24.
वृत्त में केन्द्र से समान दूरी पर स्थित जीवाओं का अनुपात (RBSESolutions.com) लिखिये। (माध्य. शिक्षा बोर्ड, 2018)
हल:
हम जानते हैं कि ”किसी वृत्त की जीवायें केन्द्र से बराबर दूरी पर हो तो वे परस्पर बराबर होती हैं।”
अतः जीवाओं का अनुपात 1 : 1 होगा।
![]()
लघूत्तरात्मक प्रश्न
प्रश्न 1.
आकृति में, वृत्त का केन्द्र 0 एवं त्रिज्या 5 सेमी. है। यदि OP ⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 सेमी. और CD = 6 सेमी. हो, तो PQ ज्ञात कीजिए।
हल:
दिया है कि OP ⊥ AB एवं OQ ⊥ CD

प्रश्न 2.
10 सेमी. त्रिज्या के एक वृत्त में, दो जीवाएँ AB = AC = 12 सेमी. हों, (RBSESolutions.com) तो जीवा BC की लम्बाई ज्ञात कीजिए।
हल:
आकृति में, ∆ABC एक समद्विबाहु त्रिभुज है। ∠BAC का समद्विभाजक AD है, अतः AD जीवा BC का लम्ब-समद्विभाजक है।

अतः जीवा BC = 2CD = 2 x 9.6 = 19.2 सेमी.
प्रश्न 3.
आकृति में, वृत्त का व्यास AB है और ∠DAB = 40° हो, तो ∠DCA ज्ञात कीजिए।
हल:
वृत्त का व्यास AB है अतः
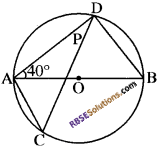
∠ADB = 90°
अब DBA = 180° – (90° + 40°) )
∠DBA = 50°
∴ ∠DBA और ∠DCA एक ही वृत्तखण्ड के कोण हैं।
अतः ∠DCA = ∠DBA = 50°
∠DCA = 50°
प्रश्न 4.
आकृति में, चाप AB और चाप AC द्वारा केन्द्र O पर अन्तरित कोण (RBSESolutions.com) क्रमशः 80° और 120° हैं। ∠BAC और ∠BOC ज्ञात कीजिए।
हल:
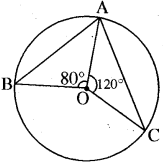
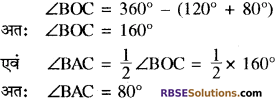
![]()
प्रश्न 5.
सिद्ध कीजिए कि एक समद्विबाहु त्रिभुज की एक समान भुजा को व्यास मानकर खींचा (RBSESolutions.com) गया वृत्त, त्रिभुज की असमान भुजा को समद्विभाजित करता है।
हल:
दिया है–
आकृति में, एक समद्विबाहु ∆ABC जिसमें AB = AC और व्यास AC पर खींचा गया वृत्त BC को D पर काटता है।
सिद्ध करना है-
BD = DC
उपपत्ति-
AC को व्यास मानकर वृत्त खींचा गया और ∠ADC अर्द्धवृत्त का कोण है,
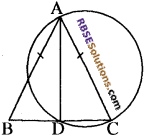
अतः ∠AIDC = 90°
अब, ∆ABD और ∆ACD में,
AB = AC (दिया है)
AD = AD (उभयनिष्ठ भुजा)
∠ADB = ∠ADNC (समकोण) .
∆ABC = ∆ACD (RHS से)
अतः सर्वांगसम त्रिभुजों की संगत भुजाएँ समान होंगी।
अर्थात् BD = CD इतिसिद्धम्
प्रश्न 6.
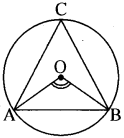
सिद्ध कीजिए कि दीर्घवृत्त खण्ड का कोण न्यूनकोण होता है।
हल:
दिया है-
आकृति में एक वृत्त, जिसका केन्द्र O है, दीर्घवृत्तखण्ड ACB है।
सिद्ध करना है-
∠ACB < 90°
रचना-
OA, OB एवं AB को मिलाया।
उपपत्ति-
चाप AB द्वारा केन्द्र पर अन्तरित कोण ∠AOB और शेष भाग पर (RBSESolutions.com) अन्तरिक कोण ∠ACB है, अतः
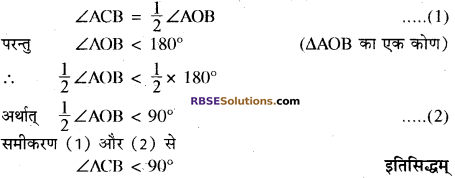
प्रश्न 7.
AOC वृत्त का एक व्यास है (RBSESolutions.com) तथा चाप AXB = \(\frac{1}{2}\) चाप BYC है। ∠BOC ज्ञात कीजिए।
हल:
क्योंकि चाप
![]()
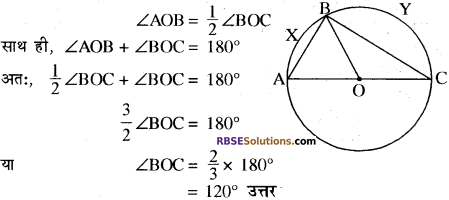
प्रश्न 8.
आकृति में, r का मान (RBSESolutions.com) ज्ञात कीजिए।
हल:
∠DAC = ∠DBC = 30° (एक ही वृत्त खण्ड में बने कोण) ….(i) ∆DBC में।
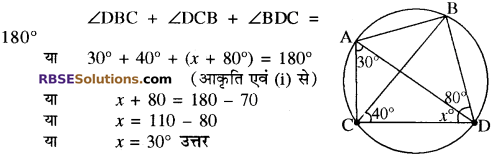
![]()
प्रश्न 9.
आकृति में, ∆BCD एक चक्रीय चतुर्भुज है। (RBSESolutions.com) यदि ∠AOC = 136° हो, तो ∠ABC ज्ञात कीजिए।
हल:
चाप ABC द्वारा केन्द्र 0 और शेष भाग पर अन्तरित कोण क्रमशः ∠AOC और ∠ADC हैं।
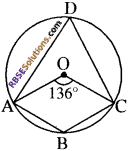
अतः ∠ADC = \(\frac{1}{2}\) ∠AOC = \(\frac{1}{2}\) x 136°
या ∠ADC = 68°
∴ ∆BCD एक चक्रीय चतुर्भुज है
अतः सम्मुख कोणों का योग 180° होगा।
∠ADC +∠ABC = 180°
∠ABC = 180° – 68°
∠ABC = 112°
प्रश्न 10.
आकृति में, ∆BCD एक चक्रीय चतुर्भुज है। x और y ज्ञात कीजिए।
हल:
चक्रीय चतुर्भुज के सम्मुख कोण (RBSESolutions.com) सम्पूरक होते हैं।
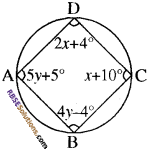
(2x + 4°) + (4° – 4″) = 180°

प्रश्न 11.
आकृति में, वृत्त का केन्द्र 0 है और चाप BCD द्वारा केन्द्र पर अन्तरित कोण 140° है।∠BAD और ∠DCE ज्ञात कीजिए।
हल:
चाप BCD द्वारा केन्द्र एवं शेष भाग पर अन्तरित कोण क्रमशः ∠BOD एवं ∠BAD हैं।
अतः ∠BAD = \(\frac{1}{2}\) x ∠BOD = x 140°_A
या ∠BAD = 70°
परन्तु ∠DCE, चक्रीय चतुर्भुज ∆BCD का बहिष्कोण है जो इसके अन्तराभिमुख कोण के बराबर होगा।
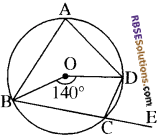
∠DCE = ∠BAD
∠DCE = 70°
प्रश्न 12.
एक चक्रीय चतुर्भुज की सम्मुख भुजाओं का युग्म समान है। (RBSESolutions.com) सिद्ध कीजिये कि उसके विकर्ण भी समान होंगे।
हल:
दिया है-
∆BCD एक चक्रीय चतुर्भुज है जिसमें AD = BC।
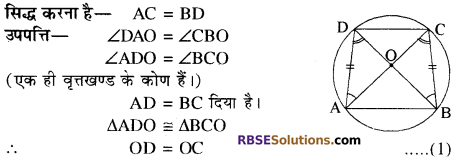
AD = BC दिया है।
∆ADO = ∆BCO
OD = OC ……….(1)
OB = OA …..(2)
समी. (1) तथा (2) को जोड़ने पर
OD + OB = OC + OA
BD = AC इतिसिद्धम्
![]()
प्रश्न 13.
सिद्ध कीजिए चक्रीय समान्तर चतुर्भुज सदैव एक (RBSESolutions.com) आयत होता है।
हल:
माना ∆BCD एक चक्रीय समान्तर DA चतुर्भुज है। समान्तर चतुर्भुज ∆BCD को आयत सिद्ध करने के लिए हम यह सिद्ध करेंगे कि इसका AF एक कोण समकोण है।

∴ ∆BCD एक समान्तर चतुर्भुज है।
∴ ∠B = ∠D …………….(1)
(∵ समान्तर चतुर्भुज के सम्मुख कोण समान होते हैं।)
पुनः ∴ ABCD एक चक्रीय चतुर्भुज है।
∴ ∠B +∠D = 180° ………(2)
समीकरण (1) तथा (2) से
∠B +∠B = 180° या 2∠B = 180°
∠B = 90° समी.
(1) से 20 = 90°
अत: ABCD एक आयत है। (इतिसिद्धम् )
प्रश्न 14.
दी गई आकृति में कुछ कोणों को r, y और z से चिह्नित किया गया है। (RBSESolutions.com) इन कोणों के मान ज्ञात कीजिए। (माध्य. शिक्षा बोर्ड, 2018)
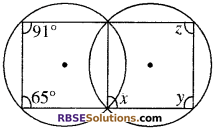
हल:
दिये गये चित्र में ∆BEF एक चक्रीय चतुर्भुज है हम जानते हैं कि चक्रीय चतुर्भुज के बहिष्कोण उसके अन्तराभिमुख कोण के बराबर होते हैं इस कारण से
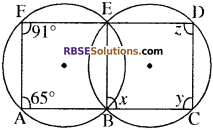
∠BAF = ∠BED = 65°
चित्र से ∠E +∠C = 180°
∵ BEDC एक चक्रीय चतुर्भुज है जिसमें आमने – सामने के कोनों (RBSESolutions.com) का योग 180° होता है।

निबन्धात्मक प्रश्न
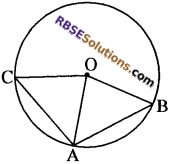
प्रश्न 1.
आकृति में, चाप AB = चाप CD है, सिद्ध (RBSESolutions.com) कीजिए कि ∠A=∠B है।
हल:
दिया है-
चाप AB = चाप CD है,
सिद्ध करना है-
∠A = ∠B
उपपत्ति-
हम जानते हैं कि समान चाप द्वारा केन्द्र पर अन्तरित कोण समान होते हैं।
अतः ∠AOB = ∠COD
दोनों पक्षों में ∠BOC जोड़ने पर
∠AOB + ∠BOC = ∠BOC + ∠COD
या ∠AOC = ∠BOD …..(1)
अब AAOC और ABOD में,
OA = OB (वृत्त की त्रिज्याएँ)
OC = OD (वृत्त की त्रिज्याएँ)
∠AOC = ∠BOD [समीकरण (1) से]
∆AOC =∠BOD (SAS से)
अतः सर्वांगसम त्रिभुजों के संगत कोण समान होंगे।
∠A =∠B इतिसिद्धम्
![]()
प्रश्न 2.
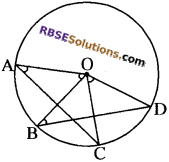
एक वृत्त की दो जीवाएँ AB और AC बराबर हैं। सिद्ध कीजिए (RBSESolutions.com) कि वृत्त का केन्द्र ∠BAC के समद्विभाजक पर स्थित होगा।
हल:
दिया है-
एक वृत्त जिसका केन्द्र O है, जिसकी जीवाएँ AB और AC समान हैं।
सिद्ध करना है-
केन्द्र O, कोण BAC के समद्विभाजक पर स्थित है।
रचना-
CO और BO को मिलाया।
उपपत्ति-
∆AOB और ∆AOC में,
B0 = 0C (वृत्त की त्रिज्याएँ)
OA = OA (उभयनिष्ठ भुजा)
AB = AC (दिया है)
∆AOB = ∆AOC (SSS से)
अतः सर्वांगसम त्रिभुजों के संगत कोण समान होंगे।
अर्थात् ∆OAB = ∠OAC
अर्थात् केन्द्र O, कोण BAC के समद्विभाजक पर स्थित है। इतिसिद्धम् ।
प्रश्न 3.
यदि दो वृत्त, एक-दूसरे को दो बिन्दुओं पर प्रतिच्छेदित करते हों, (RBSESolutions.com) तो सिद्ध कीजिए कि उनके केन्द्रों को मिलाने वाली रेखा उनकी उभयनिष्ठ जीवा का लम्ब समद्विभाजक होती है।
हल:
दिया है-
आकृति में दो वृत्त, जिनके केन्द्र क्रमशः O एवं P हैं, जो A और B बिन्दुओं पर प्रतिच्छेद करते हैं।
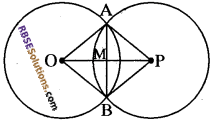
सिद्ध करना है-
OP जीवा AB का लम्बसमद्विभाजक है।
रचना-
OA, OB, PA और PB को मिलाया।
उपपत्ति-
AOAP और AOBP में,
AO = OB (एक ही वृत्त की त्रिज्याएँ)
PA = PB (एक ही वृत्त की त्रिज्याएँ)
OP = OP (उभयनिष्ठ)
∆OAP = ∆OBP (SSS से)
अतः सर्वांगसम त्रिभुजों के संगत कोण बराबर होंगे।
∠AOP = ∠BOP
या ∠AOM = ∠BOM …..(1)
अब, ∆AOM और ∆BOM में
OA = OB (एक ही वृत्त की त्रिज्याएँ हैं)
∠AOM = ∠BOM [समीकरण (1) से]
OM = OM (उभयनिष्ठ)
∆AOM = ∆BOM (SAS से)
अतः सर्वांगसम त्रिभुजों की संगत भुजाएँ एवं कोण समान होंगे।
OP, जीवा AB का लम्ब समद्विभाजक है। इतिसिद्धम्
प्रश्न 4.
सिद्ध कीजिए कि वृत्त की दो जीवाओं में से बड़ी जीवा केन्द्र के (RBSESolutions.com) निकट होती है।
हल:
दिया है-
आकृति में, एक वृत्त, जिसका केन्द्र O है और जीवा CD > जीवा AB
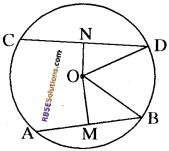
सिद्ध करना है-
ON < OM
रचना-
OB और OD को मिलाया।
उपपत्ति-
OM और ON क्रमशः AB और CD पर लम्ब हैं,

![]()
प्रश्न 5.
आकृति में, एक वृत्त में जीवा AB = जीवा CD हों, तो सिद्ध (RBSESolutions.com) कीजिए कि DQ = BQ.
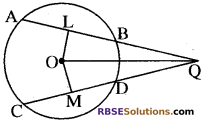
हल:
दिया है-
जीवा AB = जीवा CD
सिद्ध करना है-
DQ = BQ
रचना-
OL ⊥ AB और OM ⊥ CD खींचे और OQ को मिलाया।
उपपत्ति-
AB = CD (दिया हुआ है)
OL = OM …..(1)
∆OMQ और ∆OLQ में,
OQ = 0Q (उभयनिष्ठ भुजा)
OM = OL [समीकरण (1) से]
∠OMQ=∠OLQ (समकोण)
∆OMQ= ∆OLQ (RHS से)
अतः सर्वांगसम त्रिभुजों की संगत भुजाएँ समान होंगी।
अर्थात् MQ = LQ …………(2)
परन्तु MD = \(\frac{1}{2}\) CD और LB = \(\frac{1}{2}\) AB
AB = CD ⇒ MD =LB ……………..(3)
समीकरण (2) में से (3) को घटाने पर
MQ – MD = LQ – LB
अतः DQ= BQ इतिसिद्धम्
प्रश्न 6.
एक चतुर्भुज ∆BCD में AB = AC = AD हों, तो सिद्ध (RBSESolutions.com) कीजिए foto ∠BAD = 2(∠BDC + ∠CBD).
हल:
दिया है कि AB = AC = AD अर्थात् बिन्दु B, C और D बिन्दु A से समान दूरी पर हैं, अतः वृत्त का केन्द्र A है।
अब चाप BC केन्द्र पर ∠BAC और वृत्त के BK शेष भाग पर ∠BDC बनाता है।
∴ ∠BAC = 2∠BDC …..(1)
इसी प्रकार चाप CD केन्द्र पर ∠CAD और वृत्त के शेष भाग ∠CBD बनाता है।
∴ ∠CAD = 2∠CBD ………….(2)
समीकरण (1) और (2) का योग करने पर
∠BAC + ∠CAD = 2(∠BDC + ∠CBD)
= ∠BAD = 2(∠BDC +∠CBD) इतिसिद्धम्।
प्रश्न 7.
आकृति में, AABC एक समबाहु त्रिभुज है। इसका केन्द्र है। (RBSESolutions.com) यदि A को 0 से मिलाते हुए आगे बढ़ाया तो यह वृत्त को D पर मिलता है। सिद्ध कीजिए AOBD एक समबाहु त्रिभुज है।
हल:
दिया हुआ है-
∆ABC एक समबाहु त्रिभुज है। O, ∆ABC का केन्द्र है।
AO को आगे बढ़ाने पर वृत्त से D पर मिलता है।
सिद्ध करना-
AOBD समबाहु त्रिभुज है।
उपपत्ति-
OB एवं OD (एक वृत्त की त्रिज्याएँ)
अतः ∠OBD = ∠ODB ……….(i)
∆ABC एक समबाहु त्रिभुज है।
अतः ∠C = 60° …..(ii)
∠ADB = ∠C
[(ii) से एक ही वृत्त खण्ड पर बने कोण)]
अतः ∠ADB = 60° [(i) से]
परन्तु ∠ADB एवं ∠ODB एक ही कोण को दर्शाता है।
अतः ∠ODB = 60°
∴ ∠OBD = 60° (समीकरण (i) से]
परन्तु ∆ में तीनों कोणों का योग 180° होता है।
अतः ∆OBD का तीसरा कोण ∠BOD भी 60° का होगा।
अतः ∆OBD एक समबाहु त्रिभुज है। इतिसिद्धम्
![]()
प्रश्न 8.
आकृति में, ∆BCD एक चक्रीय चतुर्भुज है। CD के समान्तर रेखा AE खींची गई है। BA को F तक आगे बढ़ाया गया है। (RBSESolutions.com) यदि ∠ABC = 92° और ∠FAE = 20° हो, तो ∠BCD ज्ञात कीजिए।
हल:
∆BCD एक चक्रीय चतुर्भुज है अतः
∠ABC + ∠CDA = 180° BO°
या ∠CDA = 180° – 92°
या ∠CDA = 88°
परन्तु CD || AE
या ∠DAE = ∠CDA (एकान्तर कोण)
या ∠DAE = 88°
याहाँ ∠DAF = ∠FAE + ∠DAE = 20° + 88°
या ∠DAF = 108°
∠DAB = 180° – 108° = 72°
अब ∠BCD + ∠DAB = 180°
या ∠BCD = 180° – ∠DAB = 180° – 729
या ∠BCD = 108° इतिसिद्धम्
प्रश्न 9.
यदि एक चक्रीय चतुर्भुज की दो भुजाएँ समान्तर हों, (RBSESolutions.com) तो सिद्ध कीजिए कि शेष भुजाएँ बराबर होंगी और विकर्ण भी बराबर होंगे। (माध्य. शिक्षा बोर्ड, 2018)
हल:
दिया है-
चक्रीय चतुर्भुज ∆BCD में,

AB || DC है।
सिद्ध करना है-
(i) AD = BC
(ii) AC = BD
उपपत्ति-
∴ AB || DC और BC एक AK तिर्यक रेखा है,
अतः ∠ABC + ∠DCB = 180° ……………….(1)
परन्तु ABCD एक चक्रीय चतुर्भुज है,
अतः ∠ABC + ∠ADC = 180° …………………(2)
समीकरण (1) और (2) से
∠ABC + ∠DCB = ∠ABC + ∠ADC
या ∠DCB = ∠ADC ………………..(3)
अब AADC और ABCD में,
∠ADC = ∠DCB [समीकरण (3) से]
∠DAC =∠DBC (एक ही वृत्त खण्ड के कोण) और DC = DC (उभयनिष्ठ)
∆ADC = ∆BCD. (ASA से)
अतः सर्वांगसम त्रिभुजों की संगत भुजाएँ समान होंगी,
अर्थात् AD = BC
और AC = BD इतिसिद्धम्
प्रश्न 10.
आकृति में, ABCD एक चतुर्भुज है, जिसमें AD = BC और A ∠ADC = ∠BCD है। (RBSESolutions.com) सिद्ध कीजिए। ABCD एक चक्रीय चतुर्भुज है।
हल:
दिया है-
चतुर्भुज ABCD में AD = BC और ∠ADC = ∠BCD है।
सिद्ध करना है-
ABCD एक चक्रीय चतुर्भुज है।
रचना-
DN ⊥ AB और CM ⊥ AB खींचे।
उपपत्ति-
दिया है कि
∠ADC = ∠BCD
∴ ∠ADN = ∠ADC – 90° …………(1)
= ∠BCD – 90°[समीकरण (1) से]
∠ADN = ∠BCM ……………….(2)
अब AAND और AIBMC में
∠ANI) = ∠l8MC (समकोण)
∠ADN = ∠1CM [समीकरण (2) से]
ओर AD = BC (दिया है)
∴ AAND = AlBMC (AAS से)
अतः सर्वांगसम त्रिभुजों के संगत कोण समान होंगे,
अर्थात् ∠A = ∠B …………………(3)
इसी प्रकार ∠C = ∠D ……………(4)
परन्तु ∠A + ∠13 + 2 + ∠D = 360°
समीकरण (3) और (4) से,
∠B + ∠B + ∠D + ∠D = 360°
2∠B + 2∠D = 360°
∠B + ∠D = 180
ABCD एक चक्रीय चतुर्भुज है। इतिसिद्धम्
![]()
प्रश्न 11.
दिये गये चित्र में, त्रिभुज ABC है। जिसमें ∠BAC = 30° है। (RBSESolutions.com) सिद्ध कीजिए कि BC त्रिभुज ABC के परिवृत्त की त्रिज्या है, जिसका केन्द्र O है।
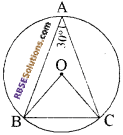
हल:
हम जानते हैं कि केन्द्र पर बना कोण शेष परिधि पर बने कोण का दुगुना होता है।
इस कारण से
∠BOC = 2 ∠BAC
∠BOC = 2 × 30°
∴ ∠BAC = 30°
∴ ∠BOC = 60°
OB = OC एक ही वृत्त की त्रिज्यायें हैं।
∠CBO = ∠BCO
हम जानते हैं
∠CBO + ∠BC) + ∠BOC = 180°
⇒ ∠CB0 + ∠BC() = 180° – ∠ BOC
⇒ ∠CBO + ABCO = 180° – 60° = 120°
लेकिन ∠CB) = ∠IBCO
अत: हम कह सकते हैं कि
∠CBO = ∠BCO = 60°
अतः त्रिभुज BOC एक समबाहु त्रिभुज होगा। इसमें OB = OC = BC लेकिन OB = OC वृत्त की त्रिज्या है।
अत: BC भी वृत्त की त्रिज्या होगी अतः BC त्रिभुज ABC के परिवृत्त की त्रिज्या है जिसका केन्द्र O है। इतिसिद्धम्
प्रश्न 12.
आकृति में ABCD एक चक्रीय चतुर्भुज है। a और b का मान ज्ञात कीजिए। (RBSESolutions.com) (माध्य. शिक्षा बोर्ड, मॉडल पेपर, 2017-18)
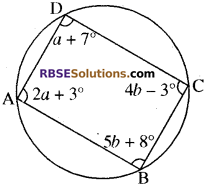
हल:
दी हुई आकृति में ABCD एक चक्रीय चतुर्भुज है इसलिए ∠A + ∠C = 180° होगा।

![]()
We hope the RBSE Solutions for Class 10 Maths Chapter 12 वृत्त Additional Questions help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 12 वृत्त Additional Questions drop a comment below and we will get back to you at the earliest.