RBSE Solutions for Class 10 Maths Chapter 14 Constructions Ex 14.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 14 Constructions Exercise 14.2.
Rajasthan Board RBSE Class 10 Maths Chapter 14 Constructions Ex 14.2
Question 1.
State wether following statements (RBSESolutions.com) are true or false. Justify your answer if possible :
(i) Circumcircle and incircle of an quadrilateral triangle can be drawn taking the same center.
(ii) All three sides of a triangle touch its in circle.
(iii) If the given triangle ¡s obtuse, its circumcenter lies on one of its sides.
(iv) The circumcentre of triangle situated inside the triangle when It is an acute triangle.
(v) To construct an incircle of a triangle, we have draw the perpendicular bisector of an two sides of the triangle to obtain the incircle.
Solution :
(i) True, since the incentre circumcentre and orthocentre of an equilateral triangle are concurrent.
(ii) True, since radius of the incircle of a triangle is equal to the perpendicular drawn from incentre to any of the side of triangle.
(iii) False, only right angled triangle has its circumcentre only on its hypotenuse.
(iv) True.
(v) False, because the incentre of a triangle is the intersecting point of bisectors of any two angles of the triangle.
![]()
Question 2.
Construct an incircle of an equilateral triangle (RBSESolutions.com) with side 4.6 cm. Give reasons if its circumcentre and incentre are concurrent.
Solution :
Given equilateral ΔPQR with its sides 4.6 cm each.
To construction : Incircle of this triangle.
Steps of construction :
(1) Draw a line segment PQ = 4.6 cm
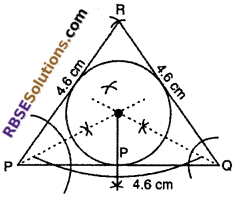
(2) Taking P as center and with 4.6 cm as radius draw an arc.
(3) Taking Q as center and with 4.6 cm as (RBSESolutions.com) radius draw another arc, which intersect each other at R.
(4) Join PQ and QR, PQR is the required equilateral triangle.
(5) Now draw the bisectors of ∠RPQ and ∠RQP, which intersect each other at O.
(6)d Draw MT ⊥ PQ from O.
(7) Taking O as centre and radius equal to OM draw a circle which touches the three sides of ΔPQR.
This is required incircie of ΔPQR.
∵ The internal angles ans sides of an equilateral triangle are equal so its circumcentre and incentre are concurrent.
Question 3.
Draw an incircle of MBC where AB = 46 cm, AC = 42 cm and ∠A = 90°.
Solution :
Given :
AB = 46 cm, AC = 4.2 cm and ∠A=90°.
To construct : Incircle of ΔABC.
Steps of construction:
(1) First of all draw a (RBSESolutions.com) line segment AB = 4.6 cm.
(2)Construct an angle of 90° at A and from mark a point C at a distance of 4.2 from A.
(3) Join BC, we get ΔABC.
(4) Draw the bisectors of ∠A and ∠B to intersects at O.
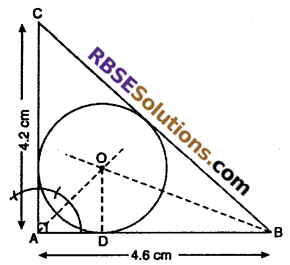
(5) Draw OD ⊥ AB from O.
(6) Taking O as center and with radius OD draw a circle which touches three sides of ΔABC
Hence, it is the incircle of ΔABC.
Question 4.
Draw a circumcircle of a triangle (RBSESolutions.com) whose sides are 10.5 cm, 12.7 cm and 13 cm respectively. Give reason, why the circumcentre of this triangle is inside the ΔABC.
Solution :
Given :
Sides of triangle arc ABC, AB = 10.5 cm, AC = 12.7 cm and BC = 13 cm.
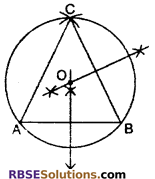
To construct:
Circumcircle of ΔABC.
(1) Taking A as center and radius 13 cm draw an arc. Taking B as center and radius 12.7 cm draw another arc which intersect the first arc at C.
(2) Join AC and BC. In this way we get ΔABC.
(3) Draw the perpendicular (RBSESolutions.com) bisectors of AB and BC which intersect each other point O. Join O and A.
(4) Taking O as center and radius equal to OA draw a circle which passes through all the three vertices of ΔABC.
Since, constructed ΔABC is an acute angled triangle so its center lies inside the circle.
![]()
Question 5.
Where should the circumcentre of a triangle with sides 5 cm, 4.5 cm and 7 cm be situated ? Show it by construction of circumcircle of this triangle.
Solution :
Given :
A triangle whose sides are 5 cm, 4.5 cm and 7 cm.
To construct : Circumcircle of this triangle.
Steps of construction:
(1) Let triangle be ABC, whose (RBSESolutions.com) sides AB = 5 cm, AC = 4.5 cm and BC = 7 cm.
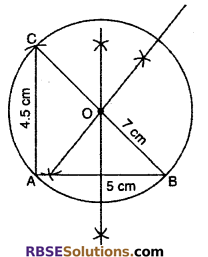
(2) From point A radius 4.6 cm drawn an arc also from point B and radius 7 cm draw another arc that intersects the first arc at C.
(3) Join AC and BC. In this way we get the ΔABC. Since it is an obtuse triangle. Thus its circumcentre will lie outside the circle.
(4) Draw the perpendicular bisectors of sides AB and BC to intersect each other at O. Which is the circumcentre of the ΔABC and is outside the triangle.
(5) Join A to O taking O as center and with radius equal to AO draw a circle which passes through three vertices of ΔABC.
This is the circumcircle of ΔABC.
Question 6.
Draw a ΔABC, in which AB = 6 cm, BC = 4 cm and (RBSESolutions.com) angle B = 120°. Construct an incircle of this triangle.
Solution :
Given :
AB = 6 cm, BC = 4 cm. and ∠B = 120°
To construct: Incircle of ΔABC
Steps of construction :
(1) Draw a line segment BC = 4 cm.
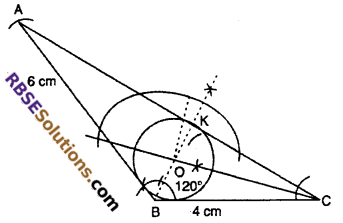
(2) Construct a ray making (RBSESolutions.com) an angle of 120° at B of BC. Cut AB = 7 cm.
(3) Join A to C, and obtain ΔABC.
(4) Now bisects ∠ABC and ∠BCA that to intersect at O.
(5) Draw OD ⊥ AC and with O as centre and OD as radius draw a circle which touches three sides of ΔABC.
This is the incircle of ΔABC.
We hope the given RBSE Solutions for Class 10 Maths Chapter 14 Constructions Ex 14.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 14 Constructions Exercise 14.2, drop a comment below and we will get back to you at the earliest.