RBSE Solutions for Class 10 Maths Chapter 15 Circumference and Area of a Circle Additional Questions

RBSE Solutions for Class 10 Maths Chapter 15 Circumference and Area of a Circle Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 15 Circumference and Area of a Circle Additional Questions.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 10
Subject	Maths
Chapter	Chapter 15
Chapter Name	Circumference and Area of a Circle
Exercise	Additional Questions
Number of Questions Solved	28
Category	RBSE Solutions

Rajasthan Board RBSE Class 10 Maths Chapter 15 Circumference and Area of a Circle Additional Questions

Multiple Choice Questions
Question 1.
If circumference of a circle and perimeter (RBSESolutions.com) of a square are same then, [NCERT Exemplar Problem]
(A) Area of circle = Area of square
(B) Area of circle > Area of square
(C) Area of circle < Area of square
(D) Nothing is definite
Solution :
(B) is correct option.

Question 2.
If sum of area of the circles of radius R₁ and R₂ is equal to the area of circle of radius R, then [NCERT Exemplar Problem]
(A) R₁ + R₂ = R
(B) R₁² + R₂² = R²
(C) R₁ + R₂ < R
(D) R₁² + R₂² < R²
Solution :
(B) is correct.

Question 3.
In fig. OACB is a quadrant of circle with center O and (RBSESolutions.com) radius 3.5 cm. If OD = 2 cm, then area of shaded part will be :

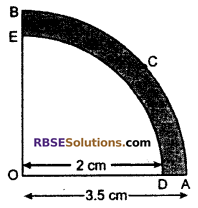
(A) 6.482 cm²
(B) 5.485 cm²
(C) 4.485 cm²
(D) 3.485 cm²
Solution :
Area of shaded part = \(\frac { 1 }{ 4 }\)π(R² – r²),
(where R = outer radius, r = Inner radius)

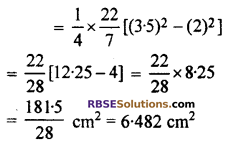
Thus, option (A) is correct.

Question 4.
Area of circle inscribed in a square of (RBSESolutions.com) side 6 cm will be : [NCERT Exemplar Problem]
(A) 36π cm²
(B) 18π cm²
(C) 12π cm²
(D) 9π cm²
Solution :
Given
Side of square ABCD = 6 cm

Radius of circle inscribe in a square of radius (r) = \(\frac { 6 }{ 2 }\) = 3 cm
Area of circle = πr²
= π × (3)²
= 9π cm
Thus (D) is correct.

Question 5.
The area of square inscribed in a (RBSESolutions.com) circle of radius 8 cm will be : [NCERT Exemplar Problem]
(A) 256 cm²
(B) 128 cm²
(C)64 \(\sqrt { 2 }\) cm²
Solution :
Given
Radius of circle (r) = 8 cm
∴ Radius of circle = 2 × 8 = 16 cm

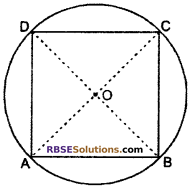
∵ We know that diagonals of square (RBSESolutions.com) inscribed in a circle bisects at center of circle.
Thus AC = 16 cm
Let side of square = x cm
In right angled triangle ABC

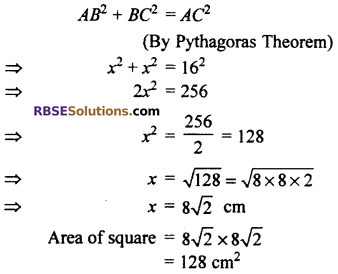
Thus option (B) is correct.

Question 6.
If perimeter of a circle is equal to the (RBSESolutions.com) perimeter of a square then ratio of their area will be : [NCERT Exemplar Problem]
(A) 22 : 7
(B) 14 : 11
(C) 7 : 22
(D) 11 : 14
Solution :
Let r is radius of circle and x is side of square.
Perimeter of circle = Perimeter of square

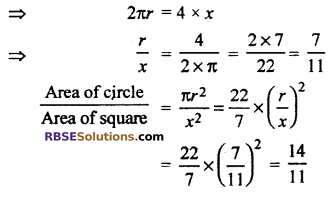
Area of circle : Area of square = 14 : 11
Thus, option (B) is correct.

Question 7.
The area of largest triangle which can be (RBSESolutions.com) drawn ¡n a semicircle of radius r : [NCERT Exemplar Problem]
(A) r²
(B) \(\frac { 1 }{ 2 }\)r²
(C) 2r²
(D) \(\sqrt { 2 }\)r²
Solution :
Let AB is diameter of semi-circle.
whose center is O and ΔABC is largest triangle which can be drawn in semicircle in which AC = BC
∠ACB = 90° (angle in semicircle is 90°)

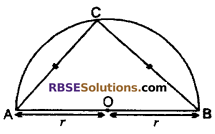
Thus, ACB is right triangle
Let AC = BC = x
Radius of (RBSESolutions.com) semicircle = r (given)
In right angled triangle ABC,

Thus, option(A) is correct.

Question 8.
If π = \(\frac { 22 }{ 7 }\), then (RBSESolutions.com) distance covered in the revolution (in m) of a wheel of radius 35 cm will be : [CBSE 2013]
(A) 2.2
(B) 1.1
(C) 9.625
(D) 96.25
Solution :
Given
Diameter of wheel = 35 cm
∴ Radius of wheel (r) = \(\frac { 35 }{ 2 }\) cm
Distance covered in 1 revolution by wheel = circumference of wheel
= 2πr
= 2 × \(\frac { 22 }{ 7 }\) × \(\frac { 35 }{ 2 }\)
= 110 cm = 1.1 m
Thus, option (B) ¡s correct.

Question 9.
The radius of a circle of circumference (RBSESolutions.com) equal to the sum of circumference of two circles of diameter 36 cm and 20 cm will be : [NCERT Exemplar problem]
(A) 56 cm
(B) 42 cm
(C) 28 cm
(D) 16 cm
Solution :
Diameters of two circles are 36 cm and 20 cm respectively so their radius r₁ = \(\frac { 36 }{ 2 }\) = 18 cm and r₂ = \(\frac { 20 }{ 2 }\) = 10 cm
Let R be the radius of required circle.
According to the question
Sum of circumference of (RBSESolutions.com) given circles = Circumference of required circle

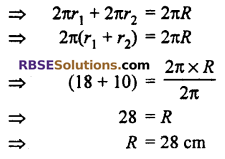
Thus, option (C) is correct.

Question 10.
The diameter of a circle of area equal to sum of areas of (RBSESolutions.com) two circles of radius 24 cm and 7 cm will be : [NCERT Exemplar Problem]
(A) 31 cm
(B) 25 cm
(C) 62 cm
(D) 50 cm
Solution :
Given :
Radius of two circles r₁ = 24 cm, r₂ = 7 cm
Let R be the radius of required circle.
According to question
Sum of areas of two given circles = area of required circle

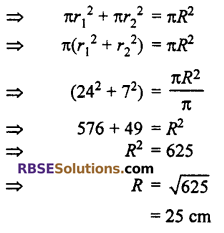
Thus, diameter of required circle = 2 × 25 = 50 cm
Thus, (D) is correct.

Short/Long Answer Type Questions

Question 1.
If radius of a circle is 14 cm, then find (RBSESolutions.com) area of circle. [M.S.N. Raj 2013]
Solution :
Given
Radius of circle (r) = 14 cm
Area of circle = πr²
= \(\frac { 22 }{ 7 }\) × (14)²
= 22 × 14 × 2
= 616 sq cm
Thus, Area of circle = 616 sq cm

Question 2.
Find the area of sector of a circle of radius r, whose (RBSESolutions.com) angle is θ in degree. (MS.B. Raj 2014)
Solution :
Area of sector of circle whose radius r and angle is in degree θ, is
= \(\frac { { \pi r }^{ 2 }\theta }{ { 360 }^{ \circ } }\)

Question 3.
A sector of circle of radius r, whose angle In degree is O. Find the length of arc. (M.S.B. Raj 2015)
Solution :
A sector of circle of radius r, whose angle in degree is 9 then length of arc (l) = \(\frac { \pi r\theta }{ { 180 }^{ \circ } } \)

Question 4.
Find the area of circle whose (RBSESolutions.com) circumference is 44 cm. (M.S.B. Raj 2014)
Solution :
Given :
Circumference of circle = 44 cm
We know that
Circumference of circle = 2πr
44 = 2 × \(\frac { 22 }{ 7 }\) × r
r = \(\frac { 44\times 7 }{ 2\times 22 }\) = 7 cm
Area of circle = πr²
= \(\frac { 22 }{ 7 }\) × 7 × 7
= 154 sq cm

Question 5.
Find the area of major sector (RBSESolutions.com) corresponding to angle 120° In circle of radius 7 cm. (M.S.B. Raj 2015)
Solution :
Given : θ = 120° radius r = 7 cm
Area of major sector

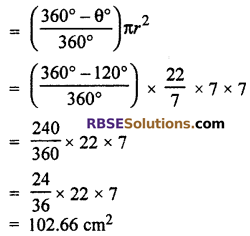
Question 6.
Find the circumference of a (RBSESolutions.com) circle of diameter 14 cm. (M.S.B. 2015)
Solution :
Given
Diameter of circle = 14 cm
We know that
Radius r = \(\frac { 14 }{ 2 }\) = 7 cm
Circumference of circle = 2πr
= 2 × \(\frac { 22 }{ 7 }\) × 7
= 44 cm

Question 7.
The diameter of a circular pond is 17.5 m. It is enclosed by a circular path of width 2 m. Find the cost of making this path at ₹ 25/m². (NCERT Exemplar Problem)
Solution :
Let O is center of circular pond whose (RBSESolutions.com) diameter is 17.5 m and it is enclosed by a 2 m broad path. So radius of circular path.

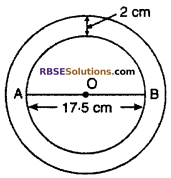
r = \(\frac { 17.5 }{ 2 }\) m
Radius of pond along with path (R)
\(\frac { 17.5 }{ 2 }\) + 2
\(\frac { 21.5 }{ 2 }\) m
Area of circular path

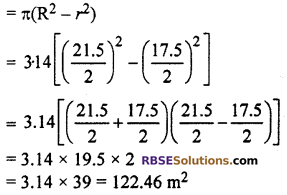
Making cost of path = 122.46 × 25 = ₹ 3061.50
Thus, cost of path = ₹ 3061.50

Question 8.
An arc of circle of radius 21 cm, subtends an (RBSESolutions.com) angle 60° at center, then find area of corresponding major sector. (BSER 2012)
Solution:
Radius (r) = 21 cm
Let arc AB subtends angle 60° at center corresponding major sector angle
θ = 360°- 60° = 300°

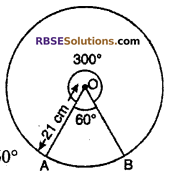
Area of corresponding major sector

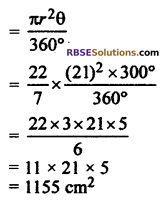
Thus area of corresponding major sector = 1155 cm²

Question 9.
Find the area of sector of circle (RBSESolutions.com) of radius 4 cm, whose angle is 60°. Also find area of corresponding major sector [π = 3.14] [M.S.R. Raj 2013]
Solution:
Radius of circle (r) = 4 cm
Angle of sector r(θ) = 60°

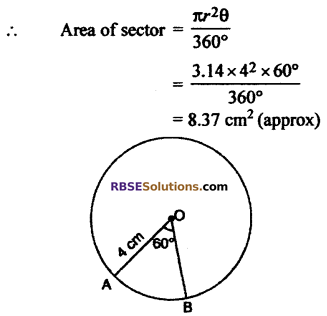
Angle of corresponding major sector = 360° – 60° = 300°
∴ Area of corresponding major sector

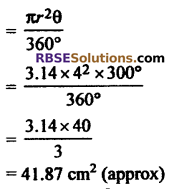
Thus area of sector = 8.37 cm² (approx)
area of major sector = 41.87 cm² (approx)

Question 10.
ln given figure, find the area of shaded part If ABCD is a (RBSESolutions.com) square of side 14 cm and APD and BPC are two semicircles. (CBSE 2012)
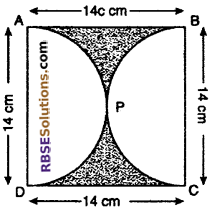Solution :
Given: Side of square = 14 cm
Diameter of semi circle (AD = CB) = 14 cm
Radius of (RBSESolutions.com) semicircle (R) = \(\frac { 14 }{ 2 }\) = 7 cm
∴ Area of square ABCD = (side)²
= 14 × 14 = 196 cm²
Area of semicircle = \(\frac { 1 }{ 2 }\)πr²
\(\frac { 1 }{ 2 }\) × \(\frac { 22 }{ 7 }\) × 7 × 7 = 77 cm²
Area of two semicircle =2 × 77 = 154 cm²
∴ Area of shaded part Area of square ABCD – Area of two semicircles
= 196 – 154 = 42 cm²
Thus area of shaded part 42 sq cm

Question 11.
From each corner of square of side 4 cm, quadrant of (RBSESolutions.com) circle of radius 1 cm is cut and also a circle of 2 cm diameter is cut from middle as shown in figure. Find the area of remaining part of square. (CBSE 2012)

Solution :
Let ABCD is a square.
Its each side = 4 cm
∴ Area of square = (side)²
= (4)² = 16 cm²
Radius of quadrant of circle (r) = 1 cm
∴ Area of four (RBSESolutions.com) quadrants = 4 × \(\frac { 1 }{ 4 }\)πr²
= πr²
= \(\frac { 22 }{ 7 }\) × (1)²
= \(\frac { 22 }{ 7 }\) sq cm
∵ Diameter of circle cut in center = 2 cm
Radius (R) = \(\frac { 2 }{ 2 }\) = 1 cm
∴ Area of circle = πr²
= \(\frac { 22 }{ 7 }\) × (1)²
= \(\frac { 22 }{ 7 }\) cm²
Now area of shaded part = Area of square – area of 4 quadrants – area of circle
= 16 – \(\frac { 22 }{ 7 }\) – \(\frac { 22 }{ 7 }\)
= \(\frac { 112-22-22 }{ 7 }\) = \(\frac { 68 }{ 7 }\)
Thus, area of shaded part = \(\frac { 68 }{ 7 }\) sq cm

Question 12.
In the following figure, find the area of shaded (RBSESolutions.com) portion. If AB = 5 cm, AC = 12 cm and O is center of circle. (MS.B. Raj. 2014)

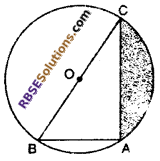
Solution :
From figure it is clear that ∠BAC is angle is semicircle.
Thus, this a (RBSESolutions.com) right angled triangle
By Pythagoras theorem,
BC² = AB² + AC²
= (5)² + (12)²
= 25 + 144
= 169
BC = 13 cm
Radius of circle R = \(\frac { 13 }{ 2 }\)cm
∴ Area of shaded portion = Area of semicircle – Area of ΔABC

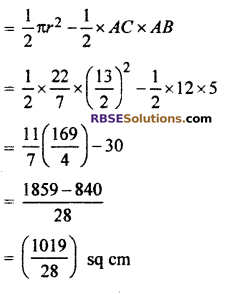
Thus, area of shaded portion = \(\frac { 1019 }{ 28 }\) sq.cm

Question 13.
Find the area of minor segment of (RBSESolutions.com) circle of radius 14 cm, whose central angle in 60°. Also find area of corresponding major segment. \(\left( \pi =\frac { 22 }{ 7 } \right) \) (CBSE 2015)
Solution :
Given : Radius of circle = 14 cm
Angle subtended chord AB at O is 60°
Now Area of circle = πr²
= \(\frac { 22 }{ 7 }\) × (14)² = 616 cm²
Area of sector AOB


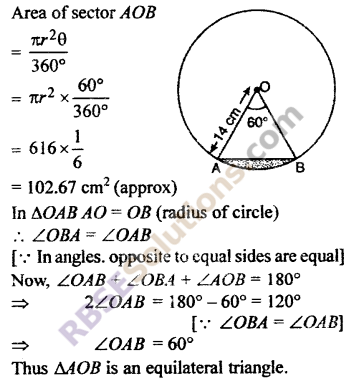
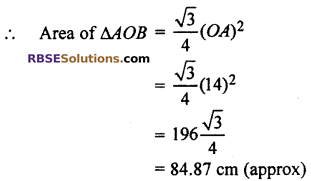
Area of minor (RBSESolutions.com) segment = A a of sector AOB – Area of ΔAOB
= 102.67 – 84.87
= 17.8 cm² (approx)
Area of major segment = Area of circle – Area of minor segment
= 616 – 17.8
= 598.2 cm²

Question 14.
In adjoining figure, OACB is a quadrant of a circle (RBSESolutions.com) with center O and radius 3.5 cm. If OD = 2 cm, then find the area of the following :
(i) Quadrant OACB
(ii) Shaded part

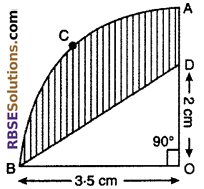
Solution :
Radius of circle (r) =3.5 cm and OD = 2 cm
(i) Area of quadrant OACB
= \(\frac { 1 }{ 4 }\) × πr²
= \(\frac { 1 }{ 4 }\) × \(\frac { 22 }{ 7 }\) × (3.5)²
= \(\frac { 38.5 }{ 4 }\) cm²
= \(\frac { 77 }{ 8 }\) cm² = 9.625 cm²
(ii) Area of quadrant OACB – Area of right triangle ΔOBD

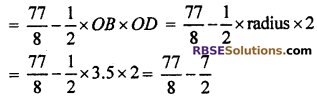
= \(\frac { 77-28 }{ 8 }\) = \(\frac { 49 }{ 8 }\) cm²= 6.125 cm²
Thus, area of shaded part = 6.125 cm²

Question 15.
In given fig, O is center of the circle in (RBSESolutions.com) which AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded part. [π = 3.14] [CBSE – 2012]
Solution :
Given : O is center of circle. So BC is diameter of circle.
∠CAB = 90° (∵ Angle in semicircle is 90°)
∴ CAB is a right angled triangle. in which AC = 24 cm and AB = 7 cm
In right angled triangle CAB
BC² = AC² + AB² (By Pythagoras Theorem)
⇒ BC² = 24² + 7²

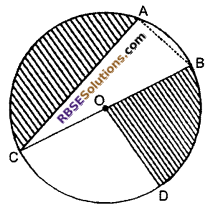
⇒ BC² = 576 + 49
⇒ BC² = 625
⇒ BC = \(\sqrt { 625 }\) = 25 cm
⇒ Radius (OC) = \(\frac { 25 }{ 2 }\) cm
Now, area of shaded part = Area of (RBSESolutions.com) semicircle – area of right angled ΔCBD + area of quadrant BOD


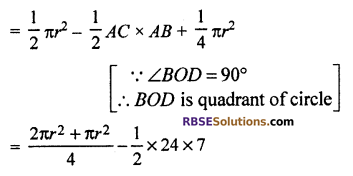
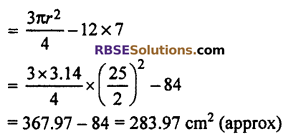
So, area of shaded part = 283.97 cm² (approx)

Question 16.
The sides of a triangles field are 15 m, 16 m and 17 m. For grazing in (RBSESolutions.com) field a cow a buffalo and a horse are tied at each corner of field by 7 m long rope separately. Find the area of that portion of field which will not be grazed by these animals. [NCERT Exemplar Problem]
Solution :
Let ABC ¡s triangular field with sides AB = 15 cm, BC = 16 m and AC = 17 m. A cow, a buffalo and a horse are tied at vertices of field A, B and C respectively and radius of each sector is 7 cm.

Question 17.
Three circles of equal radius 3.5 cm are drawn In which (RBSESolutions.com) each touches other two find the area enclosed by these circles. (NCERT Exemplar Problem)
Solution :
Taking A, B, and C as centers and radius 3.5 cm draw three circles in which each touches other two. Join AB, BC and CA.

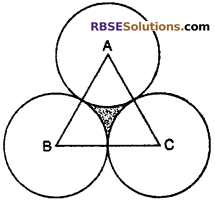
AB = 3.5 + 3.5 = 7 cm
BC = 3.5 + 3.5 = 7 cm
AC = 3.5 + 3.5 = 7 cm
Thus, ABC ¡s an equilateral triangle
∠A = ∠B = ∠C = 60°
Area of sector with center A

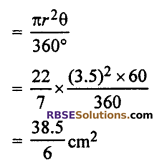
∵ Radius and angle of three (RBSESolutions.com) sectors are same
∴ Area of three sectors = \(\frac { 3\times 38.5 }{ 6 } \)
= 19.25 cm²
Area of equilateral ΔABC
= \(\frac { \sqrt { 3 } }{ 4 } \) × (side)²
= \(\frac { 1.732 }{ 4 }\) × (7)² = 21.217 cm²
Area of enclosed by three circles = Area of shaded part = Area of equilateral triangle – Area of three sectors
= 21.217 – 19.25
= 1.967 cm² (approx)
Thus, area enclosed by three cicrles = 1.967 cm² (approx)

Question 18.
In gives figure, in a quadrant OPBQ of a circle, (RBSESolutions.com) a square OABC is inscribed. If OA = 1 cm, then find area of shaded part.\(\left( \pi =\frac { 22 }{ 7 } \right) \)

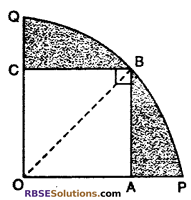
Solution :
∵ OABC is a square
∴ OA = AB = BC = OC = 21 cm
In right angled ΔOAB
OB² = OA² + AB²
= (21)² + (21)²
= 441 + 441 = 882
⇒ OB = \(\sqrt { 882 }\) = 21\(\sqrt { 2 }\) cm
∴ Radius of (RBSESolutions.com) quadrant (r) = 21\(\sqrt { 2 }\) cm
Angle of sector (θ) = 90°
Area of quadrant OPBQ

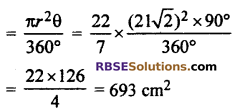
Area of square OABC = 21 × 21 = 441 cm²
∴ Area of shaded part
= Area of quadrant OPBQ – Area of square OABC
= 693 – 441 = 252 cm²
Thus area of shaded part = 252 cm²

We hope the given RBSE Solutions for Class 10 Maths Chapter 15 Circumference and Area of a Circle Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 15 Circumference and Area of a Circle Additional Questions, drop a comment below and we will get back to you at the earliest.