RBSE Solutions for Class 10 Maths Chapter 15 समान्तर श्रेढ़ी Additional Questions

RBSE Solutions for Class 10 Maths Chapter 15 समान्तर श्रेढ़ी Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 15 समान्तर श्रेढ़ी Additional Questions.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 10
Subject	Maths
Chapter	Chapter 15
Chapter Name	समान्तर श्रेढ़ी
Exercise	Additional Questions
Number of Questions Solved	43
Category	RBSE Solutions

Rajasthan Board RBSE Class 10 Maths Chapter 15 समान्तर श्रेढ़ी Additional Questions

वस्तुनिष्ठ प्रश्न 

प्रश्न 1.
संख्या है
(A) परिमेय
(B) अपरिमेय
(C) काल्पनिक
(D) इनमें से कोई नहीं
उत्तर:
(B) अपरिमेय

प्रश्न 2.
एक वृत्त की त्रिज्या 7 सेमी. है, (RBSESolutions.com) तो उसका क्षेत्रफल है
(A) 154 वर्ग सेमी.
(B) 308 वर्ग सेमी.
(C) 44 वर्ग सेमी.
(D) 606 वर्ग सेमी.
उत्तर:
(A) 154 वर्ग सेमी.

प्रश्न 3.
चित्र में वृत्त का केन्द्र 0 है। वृत्त की त्रिज्या 18 सेमी. है तथा ∠AOB = 30° है, तो लघु चाप AB की लम्बाई है

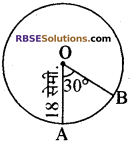
(A) 2π
(B) 3π
(C) 6π
(D) 4π
उत्तर:
(B) 3π

प्रश्न 4.
एक वृत्त की परिधि 176 सेमी. है, (RBSESolutions.com) तो उसकी त्रिज्या है
(A) 21 सेमी.
(B) 14 सेमी.
(C) 28 सेमी.
(D) 7 सेमी.
उत्तर:
(C) 28 सेमी.

प्रश्न 5.
एक वृत्तखण्ड की त्रिज्या 5 सेमी. है। इसे वृत्त के 9 सेमी. लम्बाई के चाप द्वारा बने त्रिज्यखण्ड का क्षेत्रफल है
(A) 45 वर्ग सेमी.
(B) 22.5 वर्ग सेमी.
(C) 67.5 वर्ग सेमी.
(D) 2.25 वर्ग सेमी.
उत्तर:
(B) 22.5 वर्ग सेमी.

प्रश्न 6.
एक वृत्ताकार मार्ग का बाह्य और अन्तः व्यास क्रमश: 10 मीटर व 6 मीटर है। (RBSESolutions.com) वृत्ताकार मार्ग का क्षेत्रफल है
(A) 257 वर्ग मीटर
(B) 16 वर्ग मीटर
(C) 97 वर्ग मीटर
(D) 77 वर्ग मीटर
उत्तर:
(B) 16 वर्ग मीटर

प्रश्न 7.
वृत्तखण्ड में क्षेत्रफल ज्ञात करने का सूत्र है
(A) \(\frac { \pi r ^ { 2 } \theta } { 180 ^ { \circ } } – \frac { 1 } { 2 } \sin \theta\)
(B) \(\frac { \pi r ^ { 2 } \theta } { 360 ^ { \circ } } – \frac { 1 } { 2 } r ^ { 2 } \cos \theta\)
(C) \(\frac { \pi r ^ { 2 } \theta } { 360 ^ { \circ } } – \frac { 1 } { 2 } r ^ { 2 } \sin \theta\)
(D) इनमें से कोई नहीं
उत्तर:
(C) \(\frac { \pi r ^ { 2 } \theta } { 360 ^ { \circ } } – \frac { 1 } { 2 } r ^ { 2 } \sin \theta\)

प्रश्न 8.
त्रिज्यखण्ड के चाप की (RBSESolutions.com) लम्वाई है
(A) \(\frac { 2 \pi r } { 360 } \times \theta\)
(B) \(\frac { \pi r } { 360 ^ { \circ } } \times \theta\)
(c) \(\frac { 2 r \theta } { 360 ^ { \circ } }\)
(D) \(\frac { r \theta } { 360 ^ { \circ } }\)
उत्तर:
(A) \(\frac { 2 \pi r } { 360 } \times \theta\)

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
एक वृत्त की परिधि 14 सेमी. है। इसकी त्रिज्या लिखिए।
हल:
∴ परिधि = 2πr
2πr = 14π
\(r = \frac { 14 \pi } { 2 \pi }\)
∴ r = 7 सेमी. उत्तर

प्रश्न 2.
वृत्त की परिधि किसे कहते हैं?
उत्तर:
वृत्त के अनुदिश एक पूरे चक्कर में तय की गयी दूरी को वृत्त की परिधि कहते हैं।

प्रश्न 3.
T के मान की गणना किस गणितज्ञ (RBSESolutions.com) ने की थी?
उत्तर:
भारतीय गणितज्ञ आर्यभट्ट ने के मान की गणना की थी।

प्रश्न 4.
दो संकेन्द्रीय वृत्तों द्वारा परिबद्ध क्षेत्र के क्षेत्रफल का सूत्र लिखिए।
उत्तर:
\(\pi \left( r _ { 1 } ^ { 2 } – r _ { 2 } ^ { 2 } \right) !\)

प्रश्न 5.
दो वृत्तों की त्रिज्याएँ क्रमशः 6 सेमी. और 4 सेमी. हैं। उनके क्षेत्रफलों का अनुपात लिखिए।
हल:
पहले वृत्त का क्षेत्रफल
\(\begin{array} { l } { = \pi r ^ { 2 } } \\ { = \pi ( 6 ) ^ { 2 } = 36 \pi } \end{array}\)
दूसरे वृत्त का क्षेत्रफल \(= \pi r ^ { 2 } = \pi \times ( 4 ) ^ { 2 } = 16 \pi\)
अतः क्षेत्रफलों का अनुपात = ला का अनुपात
\(= \frac { 36 \pi } { 16 \pi } = \frac { 9 } { 4 } = 9 : 4\) उत्तर

प्रश्न 6.
एक घड़ी की मिनट की सुई द्वारा 20 मिनट में केन्द्र पर (RBSESolutions.com) अन्तरित कोण का मान ज्ञात कीजिए।
हल:
घड़ी की मिनट की सुई 60 मिनट में कोण बनाती है = 360°
1 मिनट में कोण बनायेगी = \(\frac { 360 ^ { \circ } } { 60 ^ { \circ } }\)
अतः 10 मिनट में कोण बनायेगी =
\(\begin{array} { l } { = \frac { 360 ^ { \circ } } { 60 ^ { \circ } } \times 20 } \\ { = 120 ^ { \circ } } \end{array}\) उत्तर

प्रश्न 7.
उस त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए जिसके चाप की लम्बाई 10 सेमी. और त्रिज्या 6 सेमी. हो।।
हल:
यहाँ त्रिज्या = 6 सेमी., चाप (L) = 10 सेमी.
त्रिज्यखण्ड का क्षेत्रफल = \(\frac { 1 } { 2 }\) × L × r
= \(\frac { 1 } { 2 }\) × 10 × 6 = 30 सेमी. उत्तर

प्रश्न 8.
21 सेमी. त्रिज्या के वृत्त से काटे गये त्रिज्यखण्ड का कोण 60° है। (RBSESolutions.com) त्रिज्यखण्ड की चाप की लम्बाई और क्षेत्रफल ज्ञात कीजिए।
हल:
त्रिज्या r = 21 सेमी.
त्रिज्यखण्ड का कोण θ = 60°
केन्द्र पर θ कोण अन्तरित करने वाले चाप की लम्बाई
\(= \frac { \pi r \theta } { 180 ^ { \circ } } = \frac { 22 \times 21 \times 60 ^ { \circ } } { 7 \times 180 ^ { \circ } } = 22\) सेमी. उत्तर
त्रिज्यखण्ड का क्षेत्रफल = \(= \frac { \pi \mathrm { R } ^ { 2 } \theta } { 360 ^ { \circ } } = \frac { 22 \times 21 \times 21 \times 60 ^ { \circ } } { 7 \times 360 ^ { \circ } }\) वर्ग सेमी. उत्तर

प्रश्न 9.
यदि एक अर्द्धवृत्ताकार चाँदे का व्यास 14 cm. है, तो इसकी परिधि ज्ञात कीजिये।
हल:
व्यास = 14 cm., ∴ त्रिज्या (r) = \(\frac { 14 } { 2 }\) = 7 cm
परिधि \(= 2 \pi r = 2 \times \frac { 22 } { 7 } \times 7\)
= 44 cm. उत्तर

प्रश्न 10.
दो वृत्तों की परिधियों का अनुपात 2 : 3 है। (RBSESolutions.com) उनकी त्रिज्याओं का अनुपात ज्ञात कीजिये
हल:
माना दो वृत्तों की त्रिज्याएँ क्रमश: ri व r) हैं।
∴ परिधियों का अनुपात
\(= \frac { 2 \pi r _ { 1 } } { 2 \pi r _ { 2 } } = \frac { 2 } { 3 } \Rightarrow \frac { r _ { 1 } } { r _ { 2 } } = \frac { 2 } { 3 }\)
r₁ : r₂ = 2: 3 उत्तर

प्रश्न 11.
यदि एक वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप से बराबर है तो वृत्त की त्रिज्या ज्ञात कीजिये।
हल:
माना वृत्त की त्रिज्या = r है।
∴ प्रश्नानुसार वृत्त का परिमाप = वृत्त का क्षेत्रफल
2πr = πr²
r = 2 मात्रक उत्तर

प्रश्न 12.
त्रिज्या R वाले वृत्त के उस त्रिज्यखण्ड का क्षेत्रफल लिखिये जिसका कोण θ° है।
हल:
त्रिज्यखण्ड का क्षेत्रफल \(= \frac { \pi \mathrm { R } ^ { 2 } \theta ^ { \circ } } { 360 ^ { \circ } }\) वर्ग इकाई

प्रश्न 13.
r त्रिज्या वाले वृत्त के एक त्रिज्यखण्ड, जिसका कोण अंशों में से है, (RBSESolutions.com) के संगत चाप की लम्बाई लिखिये ।
हल:
कोण 8 वाले त्रिज्यखण्ड के संगत चाप की लम्बाई
\(= \frac { \theta } { 360 ^ { \circ } } \times 2 \pi r\)

प्रश्न 14.
यदि एक वृत्त की त्रिज्या 14 सेमी. हो, तो वृत्त का क्षेत्रफल ज्ञात कीजिए।
हल:
यहाँ वृत्त की त्रिज्या (r) = 14 सेमी.
∴ वृत्त का क्षेत्रफल
\(\begin{array} { l } { = \pi r ^ { 2 } } \\ { = \frac { 22 } { 7 } \times ( 14 ) ^ { 2 } = \frac { 22 } { 7 } \times 14 \times 14 } \end{array}\)
= 22 × 2 × 14 = 616 वर्ग सेमी. उत्तर

प्रश्न 15.
44 सेमी. परिधि वाले वृत्ते का क्षेत्रफल (RBSESolutions.com) ज्ञात कीजिए।
हल:
प्रश्नानुसार परिधि = 44 सेमी.
या 2πr = 44
\(\therefore r = \frac { 44 \times 7 } { 2 \times 22 } = 7\) सेमी.
∴ वृत्त का क्षेत्रफल
\(\begin{array} { l } { = \pi r ^ { 2 } } \\ { = \frac { 22 } { 7 } \times 7 \times 7 } \end{array}\)
= 154 सेमी. उत्तर

प्रश्न 16.
14 सेमी. व्यास वाले वृत्त की परिधि ज्ञात कीजिए।
हल:
∵ व्यास = 14 सेमी.
∴ त्रिज्या (r) = \(\frac { 14 } { 2 }\) = 7 सेमी.
∵ वृत्त की परिधि = 2πr
\(= 2 \times \frac { 22 } { 7 } \times 7 = 44\) सेमी. उत्तर

लघूत्तरात्मक प्रश्न

प्रश्न 1.
त्रिज्या r के एक अर्द्धवृत्त के अन्तर्गत खींचे जा सकने (RBSESolutions.com) वाले सबसे बड़े त्रिभुज का क्षेत्रफल ज्ञात कीजिये।
हल:
मानी AB अर्द्धवृत्त का व्यास है जिसका केन्द्र ) है तथा त्रिभुज ABC अर्द्धवृत्त में खींचा जा सकने वाला सबसे बड़ा ऐसा त्रिभुज है, जिसमें AC = BC होगा।
∠ACB = 90°
(अर्द्धवृत्त में बना कोण समकोण होता है)
यहाँ पर ACB समकोण त्रिभुज है। माना कि AC = BC = x
अर्द्धवृत्त की त्रिज्या = r (दिया है)
समकोण त्रिभुज ABC में,

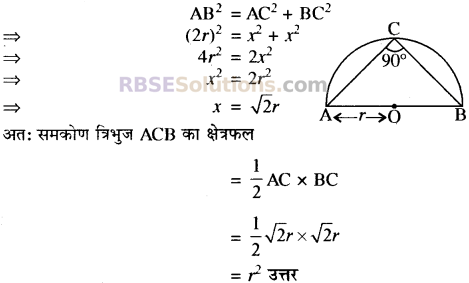
प्रश्न 2.
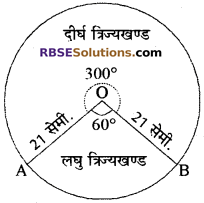
त्रिज्या 21 सेमी. वाले वृत्त का एक चाप केन्द्र पर 60° का कोण अन्तरित करता है, (RBSESolutions.com) तो संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिये।
हल:
दिया गया है–
वृत्त की त्रिज्या r = 21 सेमी.
दीर्घ त्रिज्यखण्ड चाप द्वारा बनाये गये दीर्घ त्रिज्यखण्ड का क्षेत्रफल

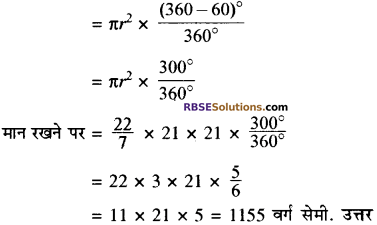
प्रश्न 3.
दी गयी आकृति में छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए, (RBSESolutions.com) जहाँ ABCD भुजा 14 cm का एक वर्ग है।

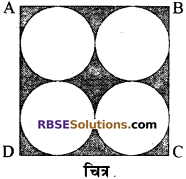
हल:

अतः छायांकित भाग का क्षेत्रफल = (196 – 154) cm² = 42 cm² उत्तर

प्रश्न 4.
7 सेमी. त्रिज्या वाले वृत्त में कोण 120° के संगत दीर्घ त्रिज्यखण्ड का (RBSESolutions.com) क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्नानुसार वृत्त के त्रिज्यखण्ड की त्रिज्या (R) = 7 cm.
केन्द्रीय कोण = 120°

प्रश्न 5.
एक वृत्त का चाप केन्द्र पर 45° का कोण अन्तरित करता है। (RBSESolutions.com) यदि इसके लघु त्रिज्यखण्ड का क्षेत्रफल 77 cm² है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
हल:
दिया है। θ = 45°
त्रिज्यखण्ड का क्षेत्रफल = 77 cm
दिया हुआ त्रिज्यखण्ड OAPB है।
त्रिज्यखण्ड का क्षेत्रफल \(= \frac { \theta } { 360 } \times \pi r ^ { 2 }\)
मान रखने पर।

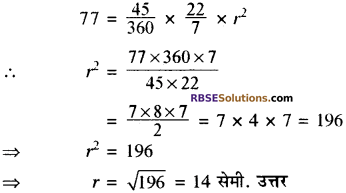
प्रश्न 6.
एक साइकिल का पहिया 11 km चलने में 5000 चक्कर लगाता है (RBSESolutions.com) तो पहिए की व्यास ज्ञात कीजिए।
हल:
पहिये द्वारा एक चक्कर में तय की गई दूरी

प्रश्न 7.
दी गई आकृति में ABC एक समबाहु त्रिभुज है, जिसकी एक भुजा 20 सेमी. है। (RBSESolutions.com) त्रिभुज के प्रत्येक शीर्ष से 10 सेमी. त्रिज्या के चाप खींचे गये हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 व \(\sqrt { 3 }\) = 1.73 लीजिए)

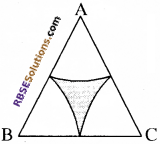
हल:
समबाहु त्रिभुज की भुजा की लम्बाई
(a) = 20 सेमी.
समबाहु त्रिभुज का क्षेत्रफल \(= \frac { \sqrt { 3 } } { 4 } \times ( 20 ) ^ { 2 }\)
समबाहु त्रिभुज का क्षेत्रफल \(= \frac { \sqrt { 3 } } { 4 }\) (भुजा)
\(\begin{aligned} & = \frac { \sqrt { 3 } } { 4 } \times 20 \times 20 \\ & = 1.73 \times 100 = 173 \end{aligned}\) सेमी².
समबाहु त्रिभुज का प्रत्येक कोण 60° होता है। (RBSESolutions.com) अतः तीनों त्रिज्य खण्डों का क्षेत्रफल समान होगा। तीनों त्रिज्य खण्डों का क्षेत्रफल

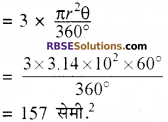
= 157 सेमी².
छायांकित भाग का क्षेत्रफल = (173 – 157) = 16 सेमी². उत्तर

प्रश्न 8.
एक घड़ी के घण्टे की सुई 6 सेमी. लम्बी है। 90 मिनट में इस सुई द्वारा बनाये गये (RBSESolutions.com) त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
हल:
घण्टे की सुई की लम्बाई = 6 सेमी.
घण्टे की सुई 6 सेमी. त्रिज्या का त्रिज्यखण्ड बनायेगी।
घण्टे की सुई द्वारा 12 घण्टे में बनाया गया कोण = 360°
घण्टे की सुई द्वारा 1 घण्टे में बनाया गया कोण = \(= \frac { 360 } { 12 } = 30 ^ { \circ }\)
घण्टे की सुई द्वारा 1 मिनट में बनाया गया कोण \(= \frac { 30 } { 60 } = \left( \frac { 1 } { 2 } \right) ^ { \circ }\)
अत. घण्टे की सुई द्वारा 90 मिनट में बनाया गया कोण \(= \left| \frac { 1 } { 2 } \right| ^ { \circ } \times 9 ( ) ^ { \circ } = 45 ^ { \circ }\)
घण्टे की सुई द्वारा निर्मित त्रिज्यखण्ड का क्षेत्रफल \(= \frac { \pi r ^ { 2 } \theta } { 360 }\)

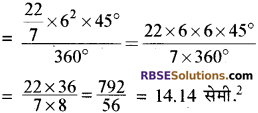
घण्टे की सुई द्वारा निर्मित त्रिज्यखण्ड का क्षेत्रफल = 14.14 सेमी². उत्तर

प्रश्न 9.
दी गई आकृति में छायांकित भाग का (RBSESolutions.com) क्षेत्रफल ज्ञात कीजिए।

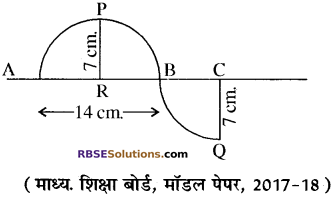
हल:
दिया है–

निबन्धात्मक प्रश्न

प्रश्न 1.
चित्र में छायांकित भाग का क्षेत्रफल ज्ञात (RBSESolutions.com) कीजिए।
हल:
दी गई आकृति में
\(P R = \sqrt { ( P Q ) ^ { 2 } + ( Q R ) ^ { 2 } }\)
\(P R = \sqrt { 16 + 9 }\) सेमी.
\(P R = \sqrt { 25 }\) सेमी.
PR = 5 सेमी.

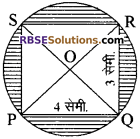
सेमी. वृत्तं की त्रिज्या \(( O P ) = \frac { P R } { 2 }\)
की त्रिज्या \(( O P ) = \frac { 5 } { 2 }\) सेमी. = 2.5 सेमी.
वृत्त का क्षेत्रफल = πr
= \(\frac { 22 } { 7 }\) × 2.5 × 2.5 सेमी².
= 19.642 सेमी.2
आयत PQRS का क्षेत्रफल = PQ × QR
= 4 × 3 सेमी = 12 सेमी².
छायांकित भाग का क्षेत्रफल = (वृत्त का क्षेत्रफल – आयत का क्षेत्रफल)
= (19.642 – 12) सेमी².
= 7.642 सेमी². उत्तर

प्रश्न 2.
चित्र में, अर्द्धवृत्त का केन्द्र O है। तथा अर्द्धवृत्त की त्रिज्या 5 सेमी. है। (RBSESolutions.com) यदि PR = 8 सेमी. हो तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

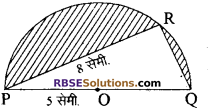
हल:
अर्द्धवृत्त का क्षेत्रफल


छायांकित भागं का क्षेत्रफल = (अर्द्धवृत्त का क्षेत्रफल – त्रिभुज PQR का क्षेत्रफल)
= (39.28 – 24) सेमी². = 15.28 सेमी².
∴ छायांकित भाग को क्षेत्रफल = 15.28 सेमी². उत्तर

प्रश्न 3.
चित्र में PQRS एक वर्ग है। जिसकी एक भुजा 7 सेमी. है। (RBSESolutions.com) वर्ग के प्रत्येक शीर्ष। पर 3.5 सेमी. त्रिज्या के वृत्त खींचे गये हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

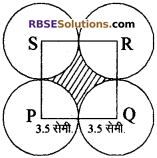
हल:
संलग्न आकृति में वर्ग की भुजा = 7 सेमी.
वर्ग का क्षेत्रफल = 7 × 7 सेमी².
= 49 सेमी².
दी गई आकृति में चारों वृत्त समान क्षेत्रफल के हैं। इन वृत्तों में त्रिज्यखण्ड कटता है।
चारों वृत्तों में त्रिज्यखण्ड का कोण (θ) = 90°
त्रिज्या (r) = 3.5 सेमी.
चारों वृत्तों के त्रिज्यखण्डों का क्षेत्रफल समान होगा।
अतः चारों त्रिज्यखण्डों का क्षेत्रफल

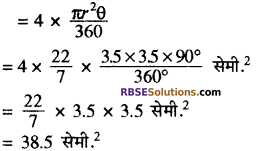
छायांकित भाग का क्षेत्रफल = (वर्ग का क्षेत्रफल – चारों क्रिज्यखण्डों का क्षेत्रफल)
= (49 – 38.5) सेमी².
= 10.5 सेमी². उत्तर

प्रश्न 4.
56 मीटर भुजा वाले एक वर्गाकार बगीचे ABCD के AB वे CD भुजा पर दो वृत्ताकार फूलों की क्यारियाँ बनाई गयी हैं। (RBSESolutions.com) यदि प्रत्येक वृत्ताकार क्यारी का केन्द्र बगीचे के विकर्णो का प्रतिच्छेद बिन्दु 0 है, तो बगीचे और क्यारियों के क्षेत्रफल का योग ज्ञात कीजिये।
हल:
वर्गाकार बगीचा ABCD का क्षेत्रफल
= भुजा × भुजा = 56 × 56 वर्ग मी. ……………………….. (i)
माना OA = OB = × मीटर है।

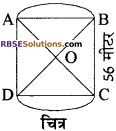
हम जानते हैं कि वर्ग के विकर्ण समकोण पर प्रतिच्छेद D करते हैं। (RBSESolutions.com) इस कारण से ∠BOA = 90°
अत: ΔAOB एक समकोण त्रिभुज है।

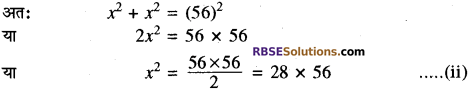
अब त्रिज्यखण्ड OAB का क्षेत्रफल

समीकरण (ii) से मान रखा है। साथ ही ΔOAB का क्षेत्रफल

∴ क्यारी AB को क्षेत्रफल

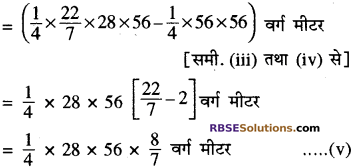
इसी तरह से दूसरी क्यारी का क्षेत्रफल

अतः सम्पूर्ण क्षेत्र = वर्ग का क्षेत्रफल + दोनों क्यारियों का क्षेत्रफल

प्रश्न 5.
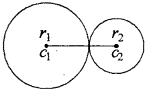
दो वृत्त बाह्यतः स्पर्श करते हैं। यदि इनके क्षेत्रफलों का योग 130 cm² है तथा इनके केन्द्रों के (RBSESolutions.com) बीच की दूरी 14 cm है, तो इन वृत्तों की त्रिज्याएँ ज्ञात कीजिये।
हल:
माना कि c₁ तथा c₂ दिये गये वृत्त के केन्द्र हैं और इनकी त्रिज्यायें क्रमश: r₁ और r₂ हैं। चूंकि दोनों वृत्त बाह्यतः स्पर्श करते हैं।


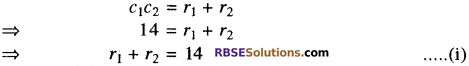
प्रश्नानुसार दोनों बूथों के क्षत्रफलों का योग = 13π cm²

समीकरण (i) तथा (iv) को जोड़ने पर ।
2r₁ = 22
∴ r₁ = 11 cm
r₁ का मान समीकरण (i) में रखने पर r₂ = 3 cm प्राप्त होता है।
अतः दोनों वृत्तों की त्रिज्यायें क्रमशः 11 cm तथा 3 cm हैं। उत्तर

प्रश्न 6.
संलग्न आकृति में AABC के शीर्ष बिन्दु A पर एक समकोण त्रिभुज है। (RBSESolutions.com) जहाँ AB = 6 cm, BC = 10 cm तथा I, त्रिभुज ABC के अन्तःवृत्त का केन्द्र है तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिये।
हल:
समकोण ∆ABC में

∴ ∆ABC का क्षेत्रफल = \(\frac { 1 } { 2 }\) × AB × AC.
⇒ ∆ABC का क्षेत्रफल = \(\frac { 1 } { 2 }\) × 6 × 8 = 24 cm² माना अन्त:वृत्त की त्रिज्या r cm है।
∴ ∆ABC का क्षेत्रफल = ∆IBC का क्षेत्रफल + ∆ICA का क्षेत्रफल :

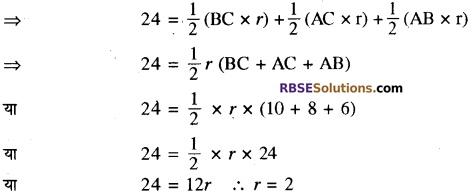
∴ छायांकित भाग का क्षेत्रफल
= ∆ABC का क्षेत्रफल = ∆IBC का क्षेत्रफल

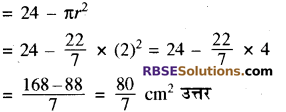
प्रश्न 7.
4 सेमी. त्रिज्या वाले एक वृत्त के उस त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, (RBSESolutions.com) जिसका कोण 60° है। साथ ही संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल भी ज्ञात कीजिए। ( π = 3.14 का प्रयोग करें।)
हल:
प्रश्नानुसार वृत्त के त्रिज्यखण्ड की त्रिज्या (R) = 4 cm. केन्द्रीय कोण (θ) = 60°

अत: त्रिजयखंड का क्षेत्रपाल = 8.37 सेमी². उतर
संगत दीर्घ त्रिजयखंड का

प्रश्न 8.
आकृति में, OACB केन्द्र O और त्रिज्या 3.5 cm. वाले एक वृत्त का चतुर्थांश है। (RBSESolutions.com) यदि OD = 2 cm. है, तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिए
(i) चतुर्थांश OACB
(ii) छायांकित भाग।

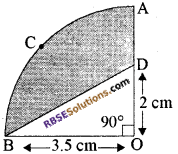
हल:
प्रश्नानुसार,
चतुर्थांश की त्रिज्या (R) = 3.5 cm.
त्रिज्यखण्ड का कोण (θ) = 90°
OD = 2 cm.
(i) चतुर्थांश OACB का क्षेत्रफल
\(= \frac { \pi \mathrm { R } ^ { 2 } \theta } { 360 ^ { \circ } }\)

∴ छायांकित क्षेत्रफल = चतुर्थांश OACB का क्षेत्रफल – ΔODB का क्षेत्रफल

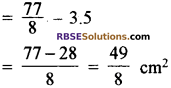
अतः छायांकित भाग का क्षेत्रफल = \(= \frac { 49 } { 8 }\) cm या 6.125 cm उत्तर

प्रश्न 9.
एक वर्गाकार रूमाल पर, नौ वृत्ताकार डिजाइन बने हैं, जिनमें (RBSESolutions.com) से प्रत्येक की त्रिज्या 7 cm. है (देखिए आकृति)। रूमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए।

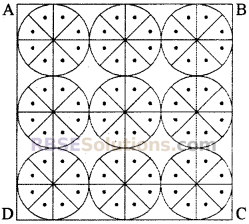
हल:
वृत्त की त्रिज्या (R) = 7 cm.
वृत्त का व्यास = 2 × R
= 2 × 7
= 14 cm,
क्योंकि वर्ग की भुजा के अनुदिश तीन वृत्त हैं।
∴ वर्ग की भुजा = 3 [14] = 42 cm.
रूमाल का कुल क्षेत्रफल = वर्ग का क्षेत्रफल = (भुजा)²
= (42)² = 1764 cm
नौ वृत्ताकार डिजाइनों का क्षेत्रफल

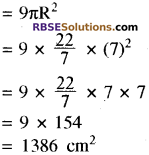
∴ शेष भाग का अभीष्ट क्षेत्रफल ।
= वर्ग का क्षेत्रफल – 9 वृत्ताकार डिजाइनों का क्षेत्रफल = 1764 – 1386
= 378 cm² उत्तर

प्रश्न 10.
एक वृत्ताकार पार्क की त्रिज्या 4.2 मीटर है। पार्क के चारों ओर 1.4 मीटर चौड़ा रास्ता बना हुआ है। (RBSESolutions.com) रास्ते का क्षेत्रफल ज्ञात कीजिए। (माध्य. शिक्षा बोर्ड, 2018)
हल:
दिया है—

We hope the RBSE Solutions for Class 10 Maths Chapter 15 वृत्त की परिधि एवं क्षेत्रफल Additional Questions help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 15 वृत्त की परिधि एवं क्षेत्रफल Additional Questions, drop a comment below and we will get back to you at the earliest.