RBSE Solutions for Class 10 Maths Chapter 2 वास्तविक संख्याएँ Additional Questions

RBSE Solutions for Class 10 Maths Chapter 2 वास्तविक संख्याएँ Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 2 वास्तविक संख्याएँ Additional Questions.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 10
Subject	Maths
Chapter	Chapter 2
Chapter Name	वास्तविक संख्याएँ
Exercise	Additional Questions
Number of Questions Solved	76
Category	RBSE Solutions

Rajasthan Board RBSE Class 10 Maths Chapter 2 वास्तविक संख्याएँ Additional Questions

विविध प्रश्नमाला 2

प्रश्न 1.
196 के अभाज्य गुणनखण्डों की घातों का योगफल है
(क) 1
(ख) 2
(ग) 4
(घ) 6
उत्तर:
(ग) 4

प्रश्न 2.
दो संख्याओं को m = pq³ तथा n = p³q² के रूप में लिखा (RBSESolutions.com)जाये तब m, n का महत्तम समापवर्तक बताइये जबकि p, q अभाज्य संख्याएँ हैं
(क) pq
(ख) pq²
(ग) p²q²
(घ) p³q³
उत्तर:
(ख) pq²

प्रश्न 3.
95 तथा 152 का महत्तम समापवर्तक (HCF) है
(क) 1
(ख) 19
(ग) 57
(घ) 38
उत्तर:
(ख) 19

प्रश्न 4.
दो संख्याओं का गुणनफल 1080 है। उनका महत्तम (RBSESolutions.com) समापवर्तक 30 है तो उनका लघुत्तम समापवर्तक है
(क) 5
(ख) 16
(ग) 36
(घ) 108
उत्तर:
(ग) 36

प्रश्न 5.
संख्या \(\frac { 441 }{ { 2 }^{ 2 }\times { 5 }^{ 7 }\times { 7 }^{ 2 } } \) का दशमलव प्रसार होगा.
(क) सांत
(ख) असांत आवर्ती
(ग) सांत एवं असांत दोनों
(घ) संख्या, परिमेय संख्या नहीं है।
उत्तर:
(ख) असांत आवर्ती

प्रश्न 6.
परिमेय संख्या 2 के दशमलव प्रसार को दशमलव के कितने अंकों के पश्चात् अंत होगा?
(क) एक
(ख) दो
(ग) तीन
(घ) चार
उत्तर:
(ग) तीन

प्रश्न 7.
सबसे न्यूनतम संख्या जिससे \(\sqrt { 27 } \) को गुणा करने (RBSESolutions.com) पर एक प्राकृत संख्या प्राप्त होती है, होगी
(क) 3
(ख) 3
(ग) 9
(घ) 343
उत्तर:
(ख) 3

प्रश्न 8.
यदि दो परिमेय संख्याओं के लिए HCF = LCM, तो संख्याएँ होनी चाहिए—
(क) भाज्य
(ख) समान
(ग) अभाज्य
(घ) सहअभाज्य
उत्तर:
(ख) समान

प्रश्न 9.
यदि a तथा 18 का LCM 36 है तथा a तथा 18 को HCF 2 है, तो a का मान होगा—
(क) 1
(ख) 2
(ग) 5
(घ) 4
उत्तर:
(घ) 4

प्रश्न 10.
यदि n एक प्राकृत संख्या है, तो 6ⁿ – 5ⁿ में इकाई का अंक है-
(क) 1
(ख) 6
(ग) 5
(घ) 9
उत्तर:
(क) 1

प्रश्न 11.
यदि \(\frac { p }{ q } \left( q\neq 0 \right) \) एक परिमेय संख्या है, तो यू पर (RBSESolutions.com) क्या प्रतिबन्ध होगा जबकि \(\frac { p }{ q } \) एक सात दशमलव हो।
हल:
हर q के अभाज्य गुणनखण्ड 2^m × 5ⁿ के रूप के होंगे, जहाँ m, n ऋणेत्तर पूर्णाक हैं।

प्रश्न 12.
सरल कर बताइए कि संख्या \(\frac { 2\sqrt { 45 } +3\sqrt { 20 } }{ 2\sqrt { 5 } } \) एक परिमेय संख्या है या अपरिमेय संख्या?
हल:
दी गयी संख्या

प्रश्न 13.
दर्शाइए कि कोई भी धनात्मक विषम पूर्णांक 4g +1 या 4g + 3 के रूप का होता है, जहाँ q कोई पूर्णाक है।
हल:
माना कि a एक धनात्मक विषम पूर्णाक है। अब a और b = 4 के लिए यूक्लिड विभाजन एल्गोरिथ्म के प्रयोग से a = 4g +r
∵ 0 ≤ r ≤ 4 अतः सम्भावित शेषफल 0, 1, 2, 3 होंगे अर्थात् a के मान 4q या 4q + 1 या 4q +2 या 4q + 3 हो सकते हैं, जहाँ q कोई भाज्य है। अब चूंकि a एक विषम धनात्मक पूर्णांक है अतः यह 4q, 4q + 2 के रूप का नहीं हो सकता क्योंकि ये सभी 2 से भाज्य होने के कारण सम धनात्मक पूर्णाक हैं । अतः कोई भी धनात्मक विषम पूर्णाक 4g + 1 या 4q+3 के रूप का होता है, जहाँ q कोई पूर्णाक है।

प्रश्न 14.
सिद्ध कीजिए कि दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 2 से भाज्य है।
हल:
माना पहला धनात्मक पूर्णांक = n
और इसके क्रमागत दूसरा धनात्मक पूर्णाक = n +1
प्रश्नानुसार हमें दोनों का गुणनफल 2 से भाज्य सिद्ध करना (RBSESolutions.com) है। अतः दोनों का गुणनफल माना f(n) = n(n + 1)
जहाँ f(x) = n²+n
हम जानते हैं कि कोई भी धनात्मक पूर्णांक 2q या (2q + 1) के रूप में होता है। जहाँ q एक पूर्णांक है।
यहाँ दो स्थितियाँ सम्भव हैं—

स्थिति I. जब n = 2q हो तो
n² + n = (2q)² + 2q
= 4q² + 2q
= 2q(2q + 1)
माना r = q(2q + 1)
⇒ n² + n = 2r

स्थिति II. जब n = 2q + 1 हो तो
n²+ n = (2q + 1)² + (2q + 1)
= 4q² + 4q + 1 + 2q + 1
= 4q² + 6q + 2
= 2(2q² + 3q + 1)
= 2r
माना r = 2q² + 3q + 1
⇒ n² + n = 2r …..(ii)
अतः समीकरण (i) व (ii) से स्पष्ट है कि
n² + n, 2 से विभाजित किया जा सकता है।
⇒ n(n + 1), भी 2 से विभाजित है।
अतः दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 2 से भाज्य है। (इतिसिद्धम् )

प्रश्न 15.
वह बड़ी से बड़ी संख्या ज्ञात कीजिए जिससे 2053 और 967 को विभाजित करने पर शेषफल क्रमशः 5 तथा 7 प्राप्त होते हैं।
हल:
यह दिया हुआ है कि 2053 को अभीष्ट पूर्णांक द्वारा विभाजित करने पर (RBSESolutions.com) शेषफल 5 रह जाता है। इसलिए 2053 – 5 = 2048 को अभीष्ट संख्या पूर्णतया भाजित करती है। अर्थात् अभीष्ट संख्या 2048 का गुणनखण्ड है। इसी प्रकार 967-7 = 960 भी अभीष्ट संख्या से विभाज्य है। चूंकि अभीष्ट संख्या सबसे बड़ी ऐसी संख्या है जो 2048 और 960 को विभाजित करती है। अतः अभीष्ट संख्या 2048 तथा 960 का महत्तम समापवर्तक है। गुणनखण्ड विधि के उपयोग से 2048 तथा 960 के अभीष्ट गुणनखण्ड निम्नानुसार हैं
2048 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2¹¹
960 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 5
= 2⁶ × 3 × 5
इसलिए 2048 और 960 का महत्तम समापवर्तक 2⁶ = 64 है।

प्रश्न 16.
व्याख्या कीजिए कि 7 × 11 × 13 + 13 और 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 भाज्य संख्याएँ क्यों हैं ?
हल:
प्रश्नानुसार
7 ×11 × 13 + 13
= 13(7 × 11 + 1)
= 13(77 + 1)
= 13 × 78
= 13 × 2 × 3 × 13
= 2 × 3 × 13 × 13
चूंकि 2, 3 और 13 अभाज्य संख्याएँ हैं। अतः अंक गणित की (RBSESolutions.com) आधारभूत प्रमेय के अनुसार प्रत्येक भाज्य संख्या अभाज्य संख्याओं के एक गुणनफल के रूप में गुणन खण्डित की जा सकती है।
अतः यह एक भाज्य संख्या है।
इसी प्रकार,
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
= 5[7 × 6 × 4 × 3 × 2 × 1 + 1]
= 5(1008 + 1) = 5 × 1009
∵ 5 और 1009 अभाज्य संख्याएँ हैं। अत: अंकगणित की आधारभूत प्रमेय के अनुसार यह एक भाज्य संख्या है।

प्रश्न 17.
यदि दो संख्याओं 306 और 657 का महत्तम समापवर्तक 9 हो, तो इनका लघुत्तम समापवर्तक ज्ञात कीजिए।
हल:
पहली संख्या = 306
दुसरी संख्या = 657
H.C.F. = 9
L.C.M. = ?
हम जानते हैं-

प्रश्न 18.
एक आयताकार बरामदा 18 मी. 72 सेमी. लम्बा तथा 13 मी. 20 सेमी. (RBSESolutions.com) चौड़ा है। इसमें समान विमाओं वाली वर्गाकार टाइलें लगानी हैं। इस प्रकार की टाइलों की न्यूनतम संख्या ज्ञात कीजिए।
हल:
आयताकार बरामदा की लम्बाई = 18 मी. 72 सेमी.
= 1800 सेमी. + 72 सेमी.
= 1872 सेमी.
इसके अभाज्य गुणनखण्ड होंगे = 2 × 2 × 2 × 2 × 3 × 3 × 13
= 2⁴ × 3² × 13
आयताकार बरामदा की चौड़ाई = 13 सेमी. 20 सेमी.
= 1300 सेमी. + 20 सेमी.
= 1320 सेमी.
इसके अभाज्य गुणनखण्ड होंगे = 2 × 2 × 2 × 3 × 11 × 5
= 2³ × 3¹ × 5 × 11
दोनों अभाज्य गुणनखण्डों का HCF = 2³ × 3¹ = 8 x 3 = 24
अतः वर्गाकार टाइल की माप होगी = 24 सेमी.
इस प्रकार से न्यूनतम वर्गाकार टाइलों की संख्या

प्रश्न 19.
सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय संख्याए हैं-

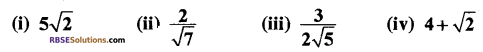
हल:
(i) प्रश्न में दिये गये कथन के विपरीत माना कि \(5\sqrt { 2 } \) एक परिमेय संख्या है। अतः हम ऐसे दो पूर्णांक a तथा b (b ≠ 0) प्राप्त कर सकते हैं कि

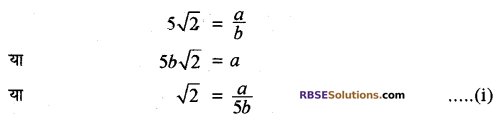
क्योंकि दो पूर्णांकों का भागफल एक परिमेय संख्या होती है।
अतः \(\frac { a }{ 5b } \) = एक परिमेय संख्या
समीकरण (i) से \(\sqrt { 2 } \) भी एक परिमेय संख्या है। परन्तु यह कथन असत्य है। अर्थात् हमारी कल्पना असत्य है। अतः \(5\sqrt { 2 } \) एक अपरिमेय संख्या है।

(इतिसिद्धम् )

(ii) \(\frac { 2 }{ \sqrt { 7 } } \)
प्रश्न में दिये गये कथन के विपरीत माना कि \(\frac { 2 }{ \sqrt { 7 } } \) एक परिमेय संख्या है।
अतः हम अविभाज्य पूर्णांक a और b(b ≠ 0) प्राप्त कर सकते हैं। अर्थात्

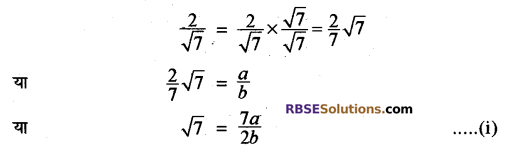
क्योंकि दो पूर्णांकों का भागफल एक परिमेय संख्या होती है।
अतः \(\frac { 7a }{ b } \) = एक परिमेय संख्या
समीकरण (i) से \(\sqrt { 7 } \) भी एक परिमेय (RBSESolutions.com) संख्या है। परन्तु यह कथन असत्य है। अर्थात् हमारी कल्पना असत्य है। अतः \(2\sqrt { 7 } \) एक अपरिमेय संख्या है।

(इतिसिद्धम्)

(iii) \(\frac { 3 }{ 2\sqrt { 5 } } \)
प्रश्न में दिये गये कथन के विपरीत माना कि \(\frac { 3 }{ 2\sqrt { 5 } } \) एक परिमेय संख्या है। अतः हम अविभाज्य पूर्णाक a और b(b ≠ 0) प्राप्त कर सकते हैं। अर्थात्

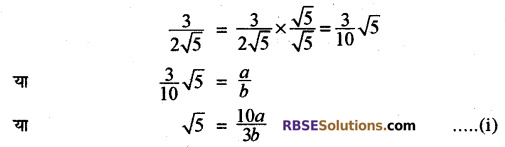
क्योंकि दो पूर्णांकों का भागफल एक परिमेय संख्या होती है।
अतः \(\frac { 10a }{ 3b } \) = एक परिमेय संख्या
समीकरण (i) से \(\sqrt { 5 } \) भी एक परिमेय संख्या है। परन्तु यह कथन असत्य है। अर्थात् हमारी कल्पना असत्य है। अतः \(\frac { 3 }{ 2\sqrt { 5 } } \) एक अपरिमेय संख्या है।

(iv) \(4+\sqrt { 2 } \)
माना कि \(4+\sqrt { 2 } \) एक परिमेय संख्या (RBSESolutions.com) है। अतः हम ऐसी सह-अभाज्य संख्यायें a और b(b ≠ 0) ज्ञात कर सकते हैं कि

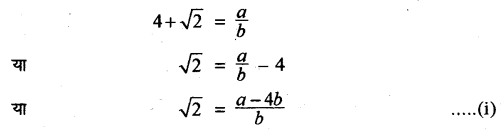
चूँकि a तथा b पूर्णांक हैं अतः \(\frac { a-4b }{ b } \) भी एक पूर्णांक संख्या होगी क्योंकि पूर्णांकों की बाकी तथा पूर्णांकों का भाग भी पूर्णांक होता है।
अर्थात्
\(\frac { a-4b }{ b } \) = एक परिमेय संख्या
इसलिए समीकरण (i) से \(\sqrt { 2 } \) = एक परिमेय संख्या
परन्तु यह कथन कि \(\sqrt { 2 } \) (RBSESolutions.com) एक अपरिमेय संख्या होती है, का विरोधाभासी कथन है।
अतः हमारी कल्पना असत्य है। अर्थात् \(4+\sqrt { 2 } \) एक अपरिमेय संख्या है।

(इतिसिद्धम्)

प्रश्न 20.
निम्न परिमेय संख्याओं के हर के अभाज्य गुणनखण्डन के बारे में आप क्या कह सकते हैं?
(i) 34.12345
(ii) \(43.\overline { 123456789 } \)
हल:

जो कि \(\frac { p }{ q } \) के रूप की एक परिमेय संख्या है।
अतः q के अभाज्य गुणनखण्ड 2 या 5 के अतिरिक्त एक और (RBSESolutions.com) गुणनखण्ड होगा। अतः दी गई संख्या परिमेय है और q के अभाज्य गुणनखण्ड 2 या 5 के अतिरिक्त भी है।
अर्थात् इसके हर का अभाज्य गुणनखण्ड 2m x 5″ के रूप का नहीं है। चूंकि इसका दशमलव प्रसार असांत आवर्ती है।

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
दो संख्याओं का HCF खोजने वाले विद्वान् गणितज्ञ यूक्लिड थे
(A) यूनान के
(B) भारत के
(C) अमेरिका के
(D) ब्रिटेन के
उत्तर:
(A) यूनान के

प्रश्न 2.
एक ऐसी संख्या जिसके 1 और स्वयं के अतिरिक्त कोई गुणनखण्ड न हो, कहलाती है
(A) भाज्य संख्या
(B) अभाज्य संख्या
(C) सम संख्या
(D) विषम संख्या
उत्तर:
(B) अभाज्य संख्या

प्रश्न 3.
सबसे छोटी अभाज्य संख्या है
(A) 5
(B) 4
(C) 3
(D) 2
उत्तर:
(D) 2

प्रश्न 4.
दो या अधिक संख्याओं का HCF (महत्तम समापवर्तक) होता है
(A) सबसे छोटा उभयनिष्ठ
(B) केवल उभयनिष्ठ
(C) सबसे बड़ी संख्या
(D) सबसे बड़ा उभयनिष्ठ
उत्तर:
(D) सबसे बड़ा उभयनिष्ठ

प्रश्न 5.
यदि मानक रूप में लिखी गयी परिमेय संख्या के हर के (RBSESolutions.com) अभाज्य गुणनखण्ड में 2 या 5 या दोनों अंकों के अतिरिक्त कोई अन्य अभाज्य गुणनखण्ड न हो, तो यह संख्या होती है-
(A) असांत दशमलव
(B) सांत दशमलव
(C) सांत व असांत दोनों
(D) उपर्युक्त में से कोई नहीं
उत्तर:
(B) सांत दशमलव

प्रश्न 6.
वास्तविक संख्याएँ कहलाती हैं
(A) केवल परिमेय संख्याएँ
(B) केवल अपरिमेय संख्याएँ
(C) परिमेय एवं अपरिमेय दोनों
(D) उपर्युक्त में से कोई नहीं
उत्तर:
(C) परिमेय एवं अपरिमेय दोनों

प्रश्न 7.
यदि किसी संख्या को है के रूप में नहीं लिखा जा सकता हो, जहाँ p और q पूर्णांक हैं और q ≠ 0 है, तो वे संख्याएँ कहलाती हैं
(A) पूर्ण संख्याएँ
(B) परिमेय संख्याएँ
(C) अपरिमेय संख्याएँ
(D) प्राकृत संख्याएँ।
उत्तर:
(C) अपरिमेय संख्याएँ

प्रश्न 8.
एक परिमेय संख्या और एक अपरिमेय संख्या का (RBSESolutions.com) योग या अन्तर कौनसी संख्या निम्न में से होती है?
(A) परिमेय संख्या
(B) अपरिमेय संख्या
(C) पूर्ण संख्या
(D) प्राकृत संख्या
उत्तर:
(B) अपरिमेय संख्या

प्रश्न 9.
संख्या n² – 1, 8 से विभाज्य होती है, यदि n है एक
(A) पूर्णांक
(B) प्राकृत संख्या
(C) विषम संख्या
(D) सम संख्या
उत्तर:
(C) विषम संख्या

प्रश्न 10.
यदि n² एक सम संख्या है तो n भी एक
(A) विषम संख्या है
(B) सम संख्या है।
(C) कह नहीं सकते
(D) इनमें से कोई नहीं
उत्तर:
(B) सम संख्या है।

प्रश्न 11.
एक शून्येतर परिमेय संख्या और एक (RBSESolutions.com) अपरिमेय संख्या का गुणन होता है
(A) सदैव अपरिमेय संख्या
(B) सदैव परिमेय संख्या
(C) परिमेय या अपरिमेय संख्या
(D) एक
उत्तर:
(A) सदैव अपरिमेय संख्या

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
यूक्लिड विभाजन प्रमेयिका क्या है?
उत्तर:
यदि a तथा b दो धनात्मक पूर्णांक हैं तो दो अद्वितीय पूर्णांक १ तथा r इस प्रकार होते हैं कि
a = bq +r
जबकि 0 ≤ r ≤ b

प्रश्न 2.
यूक्लिड विभाजन एल्गोरिथ्म क्या है?
उत्तर:
यह दो संख्याओं का महत्तम समापवर्तक (HCF) ज्ञात करने की एक विधि है। यह विधि यूक्लिड की एल्गोरिथ्म के नाम से जानी जाती है।

प्रश्न 3.
धनात्मक पूर्णांकों के दो महत्वपूर्ण गुण कौनसे हैं?
उत्तर:

1. यूक्लिड विभाजन एल्गोरिथ्म (कलन विधि),
2. अंकगणित की आधारभूत प्रमेय।।

प्रश्न 4.
अंकगणित की आधारभूत प्रमेय क्या है?
उत्तर:
प्रत्येक भाज्य संख्या को एक अद्वितीय रूप से अभाज्य (RBSESolutions.com) संख्याओं के गुणनफल के रूप में व्यक्त किया जा सकता है। यही तथ्य अंकगणित की आधारभूत प्रमेय कहलाती है।

प्रश्न 5.
एक शून्येत्तर परिमेय संख्या और एक अपरिमेय संख्या का गुणनफल या भागफल कौनसी संख्या होती है?
उत्तर:
एक अपरिमेय संख्या।

प्रश्न 6.
अपरिमेय संख्याओं के उदाहरण दीजिए।
उत्तर:
\(\sqrt { 2 } ,\quad \sqrt { 3 } ,\quad \sqrt { 5 } \) आदि।

प्रश्न 7.
भाज्य संख्या किसे कहते हैं?
उत्तर:
वह संख्या जिसके कम से कम एक गुणनखण्ड 1 और स्वयं के अतिरिक्त हो, भाज्य संख्या कहलाती है।

प्रश्न 8.
लघुत्तम समापवर्त्य (LCM) क्या होता है?
उत्तर:
दो या अधिक संख्याओं का लघुत्तम समापवर्त्य (LCM) वह छोटी से छोटी संख्या होती है जो प्रत्येक संख्या की गुणन है।

प्रश्न 9.
महत्तम समापवर्तक (HCF) क्या होता है?
उत्तर:
दो या दो से अधिक संख्याओं का महत्तम (RBSESolutions.com) समापवर्तक (HCF). वह सबसे बड़ी संख्या होती है जो दी गई सभी संख्याओं को पूर्णतः विभाजित करती है।

प्रश्न 10.
यदि दो संख्याएँ a तथा b दी गई हों तो इनका गुणनफल किसके बराबर होता है?
उत्तर:
HCF (a, b) × LCM (a, b)

प्रश्न 11.
संख्या 32760 को गुणनखण्डों के गुणनफल के रूप में लिखिए।
उत्तर:
32760 = 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13
= 2³ × 3² × 5 × 7 × 13

प्रश्न 12.
वास्तविक संख्याओं को परिभाषित कीजिये।
उत्तर:
वास्तविक संख्याएँ-समस्त परिमेय और समस्त अपरिमेय संख्याओं के सम्मिलित संग्रह या समूह को वास्तविक संख्याओं का समूह कहते हैं।

प्रश्न 13.
सांत दशमलव प्रसार की शर्त लिखिये।
उत्तर:
माना कि \(x=\frac { p }{ q } \) एक ऐसी (RBSESolutions.com) परिमेय संख्या है कि ५ का अभाज्य गुणनखण्ड 2ⁿ 5^m के रूप का है, जहाँ n, m ऋणेतर पूर्णांक है तो x का दशमलव प्रसार सांत होता है।

प्रश्न 14.
48 और 105 का महत्तम समापवर्तक ज्ञात कीजिए।
उत्तर:
48 और 105 48 के अभाज्य गुणनखण्ड = 2 × 2 × 2 × 2 × 3
= 2⁴ × 3
105 के अभाज्य गुणनखण्ड= 3 × 5 × 7
अतः दोनों में अधिकतम उभयनिष्ठ राशि 3 है। अतः इसका महत्तम समापवर्तक 3 होगा। उत्तर

प्रश्न 15.
क्या दो संख्याओं का म.स. (H.C.F) 15 तथा ल.स. (L.C.M.) 175 हो सकता है? कारण दीजिये।
हल:
चूँकि हम जानते हैं कि (L.C.M.), H.C.F से विभाज्य होता है। लेकिन यहाँ पर (L.C.M.) 175, (H.C.F) 15 से विभाज्य नहीं है। अतः दो संख्याओं का म.स. (H.C.F) 15 तथा ल.स. (L.C.M.) 175 नहीं हो सकता है।

प्रश्न 16.
परिमेय संख्या \(\frac { 17 }{ 8 } \) को बिना (RBSESolutions.com) लम्बी विभाजन प्रक्रिया किये दशमलव प्रसार सांत में लिखिये।
हल:
माना कि \(x=\frac { 17 }{ 8 }\) हैं
इसको इस प्रकार से लिख सकते हैं-

प्रश्न 17.
संख्या \(\frac { 3 }{ 625 } \) को दशमलव प्रसार (RBSESolutions.com) सांत है या असांत आवर्ती इसे दशमलव रूप में लिखें।
उत्तर:

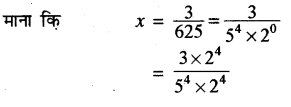
यहाँ पर q का अभाज्य गुणनखण्ड 2ⁿ5^m के रूप का है। जहाँ n, m ऋणेत्तर पूर्णांक हैं, तो x का दशमलव प्रसार सांत होता है।

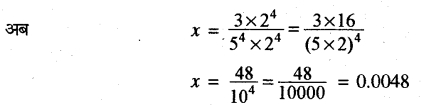
प्रश्न 18.
अभाज्य गुणनखण्ड विधि द्वारा पूर्णांक 375 और 675 का HCF ज्ञात कीजिए।
हल:
पूर्णांक 375 और 675 के अभाज्य गुणनखण्ड करने पर

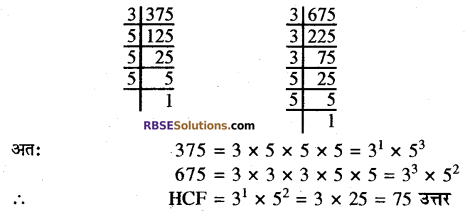
प्रश्न 19.
एक अशून्य-परिमेय संख्या तथा एक, अपरिमेय संख्या (RBSESolutions.com) का गुणनफल तथा भागफल किस तरह की संख्या होती है?
उत्तर:
अपरिमेय संख्या होती है।

प्रश्न 20.
यदि कोई बड़ी संख्या अपने आधे से कम अभाज्य संख्या से (RBSESolutions.com) भाज्य नहीं है, तब संख्या कैसी होगी?
उत्तर:
तब यह संख्या अभाज्य है अन्यथा यह भाज्य है।

प्रश्न 21.
परिमेय संख्या \(\frac { 27 }{ 2\times { 5 }^{ 2 } } \) के दशमलव प्रसार में दशमलव के कितने अंकों के पश्चात् अंत होगा? (माध्य. शिक्षा बोर्ड, मॉडल पेपर, 2017-18)
हल:

प्रश्न 22.
196 के अभाज्य गुणनखण्डों की घातों का योगफल लिखिये (माध्य. शिक्षा बोर्ड, 2018)
हल:
96 के अभाज्य गुणनखण्ड = 2 × 2 × 7 × 7
= 2² x 7²

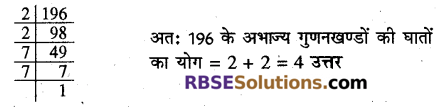
लघूत्तरात्मक प्रश्न

प्रश्न 1.
दर्शाइए कि कोई भी धनात्मक पूर्णाक 3q या 3q+1 या 3q + 2 के रूप में लिखा जा सकता है, जहाँ ५ कोई पूर्णाक है।
हल:
माना कि a कोई धनात्मक पूर्णांक है तथा b = 3 है। a तथा b = 3 पर यूक्लिड विभाजनं प्रमेयिका प्रयुक्त करने पर,
a = 3q +r
जबकि 0 ≤ r ≤ 3 तथा q कोई पूर्णांक है।
⇒ a = 3q > 0 या a = 3q + 1
या a = 3q + 2 [∵ r एक धनात्मक पूर्णाक है ।]
⇒ a = 3q या a = 3q + 1 या a = 3q + 2
किसी भी पूर्णांक q के लिए।

प्रश्न 2.
दर्शाइये कि प्रत्येक धनात्मक समं पूर्णांक 2q के रूप का (RBSESolutions.com) होता है तथा प्रत्येक धनात्मक विषम पूर्णांक 2q +1 के रूप का होता है जहाँ q कोई पूर्णाक है।
हल:
माना कि a कोई धनात्मक पूर्णांक है तथा b = 2 है। अब यदि यूक्लिड विभाजन प्रमेयिका से दो पूर्णांक q तथा r इस प्रकार विद्यमान हैं कि
a = 2q +r
जबकि 0 ≤ r < 2
अब, 0 ≤ r < 2
⇒ 0 ≤ r ≤ 1
⇒ r = 0 या r = 1 [∵ r एक पूर्णांक है]
∴ a = 2q या a = 2q + 1
यदि a = 2q है तो यह एक सम पूर्णाक है।
∵ कोई पूर्णांक या तो सम हो सकता है या विषम हो सकता है।
अतः कोई भी धनात्मक विषम पूर्णांक 2q + 1 के रूप का होगा।

प्रश्न 3.
दर्शाइये कि एक ध्रनात्मक विषम पूर्णाक 4q +1 या 4q +3 के रूप का होता है, जहाँ a कोई पूर्णाक है।
हल:
माना कि a कोई धनात्मक पूर्णांक है तथा b = 4 है। a तथा b = 4 पर यूक्लिड विभाजन प्रमेयिका प्रयुक्त करने पर दो पूर्णांक q तथा । इस प्रकार होते हैं कि
a = 4q +r
जबकि 0 ≤ r < 4
⇒ a = 4q या a = 4q + 1
या a = 4q + 2 या a = 4q + 3

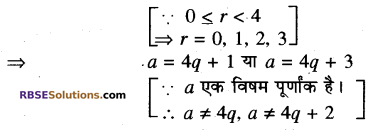
अतः कोई भी विषम पूर्णांक 4q + 1 या 4q + 3 के रूप का होगा ।

प्रश्न 4.
सिद्ध कीजिए कि प्रत्येक तीन क्रमागत धनात्मक (RBSESolutions.com) पूर्णाकों में से एक 3 से विभाज्य है।
हल:
माना कि n, n+ 1 तथा n + 2 तीन क्रमागत धनात्मक पूर्णांक हैं।
∴ n, 3q या 3q + 1 या 3q + 2 के रूप का होता है। इस स्थिति में निम्न तीन स्थितियाँ हैं-
स्थिति I: जब n = 3q है।
इस स्थिति में n, 3 से विभाज्य है परन्तु n + 1 तथा n + 2, 3 से विभाज्य नहीं है।
स्थिति II : जब n = 3q + 1
इस स्थिति में n + 2 = 3q + 1 + 2 = 3(q+ 1), जो कि 3 से विभाज्य है परन्तु n तथा n +1 का 3 से विभाज्य नहीं है।
स्थिति III : जब n = 3q + 2 है।
इस स्थिति में n + 1 = 3q + 2 + 1 = 3(q + 1), 3 से विभाज्य है परन्तु n तथा n + 2 का 3 से विभाज्य नहीं है।
अतः n, n + 1 तथा n + 2 में से एक 3 से विभाज्य है।

प्रश्न 5.
81 और 27 का महत्तम समापवर्तक (HCF) यूक्लिड विभाजन विधि का प्रयोग कर ज्ञात कीजिए।
हल:
81 और 237
चरण I: यहाँ पर दिये गये पूर्णांक 81 एवं 237 इस प्रकार हैं कि 237 > 81, अतः इन पूर्णाकों पर यूक्लिड विभाजन विधि का प्रयोग करने पर निम्न प्राप्त होता है-
237 = 81 × 2 + 75 ……….(i)
चरण II: यहाँ शेषफल 75 ≠ 0 है। अतः भाजक 81 एवं शेषफल 75 पर यूक्लिड विभाजन विधि का प्रयोग करने पर
81 = 75 × 1 + 6 …..(ii)
चरण III: समीकरण (ii) से स्पष्ट है कि यहाँ भी शेषफले 6 ≠ 0 है। | अतः पुनः भाजक 75 एवं शेषफल 6 पर यूक्लिड विभाजन विधि का प्रयोग करेंगे अर्थात्
75= 6 × 12 + 3 …..(iii)
चरण IV: यहाँ पर भी शेषफल 3 ≠ 0 है। अतः यूक्लिड विभाजन विधि के भाजक 6 एवं शेषफल 3 पर प्रयोग करने पर हमें प्राप्त होता है-
6 = 3 × 2 + 0 …..(iv)
समीकरण (iv) से स्पष्ट है कि इस स्थिति में शेषफले 0 (शून्य) प्राप्त हो गया है। अतः अन्तिम भाजक 3 ही 81 एवं 237 का महत्तम समापवर्तक (HCF) है।

प्रश्न 6.
एक मिठाई विक्रेता के पास 420 काजू की बर्फियाँ और 130 बादाम की बर्फियाँ हैं। वह इनकी ऐसी ढेरियाँ बनाना चाहता है कि प्रत्येक ढेरी में बर्फियों की संख्या समान रहे तथा ये ढेरियाँ बफ की परात में न्यूनतम स्थान घेरें । इस काम के लिए, प्रत्येक ढेरी में कितनी बर्फियाँ रखी जा सकती हैं?
हल:
यह कार्य जाँच और भूल विधि से किया जा सकता है। परन्तु इसे एक क्रमबद्ध रूप से करने के लिए हम HCF (420, 130) ज्ञात करते हैं। तब, इस HCF से प्रत्येक ढेरी में रखी जा सकने वाली बर्फियों की अधिकतम संख्या प्राप्त होगी, जिससे ढेरियों की संख्या न्यूनतम होगी और परात में ये बर्फियाँ न्यूनतम स्थान घेरेंगी।
अब यूक्लिड एल्गोरिथ्म का प्रयोग करने पर
420 = 130 × 3 + 30
130 = 30 × 4 + 10
30 = 10 × 3 + 0
अतः 420 और 130 का HCF 10 है। इसलिए, प्रत्येक प्रकार (RBSESolutions.com) की बर्फियों के लिए मिठाई विक्रेता दस-दस की ढेरी बना सकता है। उत्तर

प्रश्न 7.
जाँच कीजिये कि क्या किसी प्राकृत संख्या n के लिए संख्या 6″ अंक शून्य पर समाप्त हो सकती है?
हल:
हम जानते हैं कि कोई भी धनात्मक पूर्णाक जिसका इकाई अंक शून्य होता है, वह अंक 5 से भाज्य होता है। अर्थात् उस धनात्मक पूर्णांक का गुणनखण्ड 5 होना चाहिए। यहाँ पर किसी n के लिए 6ⁿ धनात्मक पूर्णांक है जो शून्य पर समाप्त होता है अतः गुणनखण्डन करने पर 6ⁿ = (2 × 3)= 2ⁿ × 3ⁿ प्राप्त होता है।

इस प्रकार 6ⁿ के गुणनखण्ड में 2 एवं 3 के अतिरिक्त अभाज्य गुणनखण्ड नहीं हैं अर्थात् गुणनखण्ड में अंक 5 नहीं है। अतः 6ⁿ किसी भी प्राकृत संख्या n के लिए 0 (शून्य) अंक पर समाप्त नहीं होगा।

प्रश्न 8.
निम्नलिखित धनात्मक पूर्णांकों को अभाज्य गुणनखण्डों के (RBSESolutions.com) गुणनफल के रूप में व्यक्त कीजिए-
(i) 5005
(ii) 7429
हल:

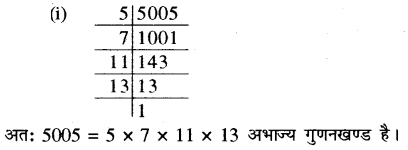
प्रश्न 9.
अभाज्य गुणनखण्डन विधि द्वारा 144, 180 और 192 के HCF एवं LCM ज्ञात कीजिए।
हल:
144 = 2 × 2 × 2 × 2 × 3 × 3 = 2⁴ × 3²
180 = 2 × 2 × 3 × 3 × 5 = 2² × 3² × 5
तथा 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3 = 26 × 31
HCF ज्ञात करने के लिए हम उभयनिष्ठ अभाज्य गुणनखण्ड की सबसे छोटी घात ज्ञात करते हैं।
अतः HCF = 2² ×3¹ = 4 × 3 = 12 उत्तर
अब लघुत्तम समापवर्तक LCM ज्ञात करने के लिए हम संख्याओं के अभाज्य गुणनखण्डों की अधिकतम घातांकों को लेते हैं।
अतः LCM = 2⁶ × 3² × 5
= 64 × 9 × 5 = 2880 उत्तर

प्रश्न 10.
पूर्णांकों के युग्म (510, 92) के HCF एवं LCM ज्ञात कीजिये तथा (RBSESolutions.com) इसकी जाँच कीजिये कि युग्म की दोनों संख्याओं का गुणनफल = HCF × LCM है।
हल:
अभाज्य गुणनखण्डन विधि से हम युग्म की संख्याओं को निम्न प्रकार लिख सकते हैं-
510 = 2 × 3 × 5 × 17 = 2¹ × 3¹ × 5¹ × 17¹
92 = 2 × 2 × 23 = 2² × 23¹
∴ HCF = 2
अब
LCM = 2² × 3¹ × 5¹ × 17¹ × 23¹
= 4 × 3 × 5 × 17 × 23
= 23460
सत्यापन-
LCM × HCF = 23460 × 2
= 46920
संख्याओं का गुणन = 510 × 92
= 46920
अतः LCM × HCF = संख्याओं का गुणनफल ( इतिसिद्धम् )

प्रश्न 11.
सिद्ध कीजिये कि \(7\sqrt { 5 } \) एक अपरिमेय संख्या है।
हुल
माना \(7\sqrt { 5 } \) एक परिमेय संख्या है।
इसलिए \(7\sqrt { 5 } =\frac { a }{ b } \)
जहाँ पर b ≠ 0 और a, b सहअभाज्य पूर्णांक संख्यायें हैं।
या \(\sqrt { 5 } =\frac { a }{ 7b } \) …..(i)
चूँकि a, b पूर्णांक हैं इसलिए \(\frac { a }{ 7b } \) एक परिमेय संख्या है। अत: समीकरण (i) से स्पष्ट है कि \(\sqrt { 5 } \) एक परिमेय संख्या होगी जो कि विरोधाभास कथन है। क्योंकि हम जानते हैं कि \(\sqrt { 5 } \) तो अपरिमेय संख्या होती है। अतः हमारी परिकल्पना कि \(7\sqrt { 5 } \) एक परिमेय संख्या है, (RBSESolutions.com) गलत है। इससे सिद्ध होता है कि \(7\sqrt { 5 } \) एक अपरिमेय संख्या है।

प्रश्न 12.
सिद्ध कीजिये कि \(3+2\sqrt { 5 } \) एक अपरिमेय संख्या है।
उत्तर:
माना कि \(3+2\sqrt { 5 } \) एक परिमेय संख्या है।
इसलिए \(3+2\sqrt { 5 } \) = \(\frac { a }{ b } \) b ≠ 0
जहाँ a, b पूर्णांक सह अभाज्य संख्यायें हैं।
समीकरण (i) को इस प्रकार से भी लिख सकते हैं-

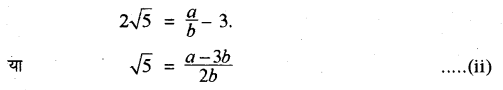
चूँकि a, b पूर्णांक संख्यायें हैं, अतः \(\frac { a-3b }{ 2b } \) एक परिमेय संख्या प्राप्त होगी। अतः समीकरण (ii) से परिणाम प्राप्त होता है कि \(\sqrt { 5 } \) एक परिमेय संख्या है। जबकि हम जानते हैं कि \(\sqrt { 5 } \) तो अपरिमेय संख्या है। अतः परिणाम विरोधाभासी है। अतः हमारी परिकल्पना कि \(3+2\sqrt { 5 } \) परिमेय संख्या है, गलत है। इससे सिद्ध होता है कि \(3+2\sqrt { 5 } \) एक अपरिमेय संख्या है।

प्रश्न 13.
लम्बी विभाजन विधि के बिना बताइये कि निम्न परिमेय संख्याओं के दशमलव प्रसार सांत हैं या असांत आवर्ती हैं-

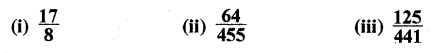
हल:

प्रश्न 14.
वह सबसे बड़ी संख्या ज्ञात कीजिए जो 247 और 2055 को इस प्रकार (RBSESolutions.com)विभाजित करती है कि प्रत्येक स्थिति में शेषफल 7 प्राप्त हो। (माध्य. शिक्षा बोर्ड, मॉडल पेपर, 2017-18)
हल:
दिया गया है कि 247 और 2055 को अभीष्ट संख्या से विभाजित करने पर प्रत्येक स्थिति में शेषफल 7 प्राप्त होता है। अत: 247 -7 = 240 एवं 2055 -7 = 2048

अर्थात् 240 और 2048 को अभीष्ट संख्या द्वारा पूर्णतया विभाजित किया जा सकता है। यह तभी सम्भव है जबकि अभीष्ट संख्या 240 एवं 2048 का उभयनिष्ठ गुणनखण्ड हो। यह भी ज्ञात है कि अभीष्ट संख्या इस उभयनिष्ठ गुणनखण्ड में
सबसे बड़ी संख्या है। अर्थात् अभीष्ट संख्या 240 एवं 2048 का महत्तम समापवर्तक | (HCF) होगी। अतः यूक्लिड विभाजन विधि का चरणबद्ध प्रयोग करने पर
2048 = 240 × 8 + 128
240 = 128 × 1 + 112
128 = 112 × 1 + 16
112 = 16 × 7 + 0
स्पष्ट है कि अन्तिम शेषफल शून्य प्राप्त हो गयी है। इस प्रकार अभीष्ट महत्तम समापवर्तक भाजक 16 प्राप्त हुआ, जो कि अभीष्ट संख्या है।

प्रश्न 15.
यदि दो संख्याओं का गुणनफल 525 है और उनका महत्तम समापवर्तक 5 है, तो उनका लघुत्तम समापवयं ज्ञात कीजिए। (माध्य. शिक्षा बोर्ड, 2018)
हल:
दिया है-
दो संख्याओं का गुणनफल = 525
उनका महत्तम समापवर्तक = 5
हम जानते हैं-

निबन्धात्मक प्रश्न

प्रश्न 1.
यूक्लिड विभाजनं प्रमेयिका का प्रयोग कर दर्शाइये कि किसी धनात्मक पूर्णाक का वर्ग 3m या 3m +1 के रूप का होता है, जहाँ m कोई पूर्णांक है।
हल:
माना a कोई धनात्मक पूर्णांक है। हम जानते हैं कि यह धनात्मक(RBSESolutions.com)  पूर्णांक a = 3q या a = 3q + 1 या a = 3q + 2 के रूप का होगा।
(i) यदि a = 3q है, तब
(a)² = (3q)² = 9q² = 3(3q²) = 3m ….(i)
जहाँ m = 3q² है।
(ii) यदि a = 3q + 1 है तब
a² = (3q + 1)² = 9q² + 6q + 1
a² = 3(3q² + 2q) + 1
= 3m +1 ….(ii)
जहाँ m = 3q² + 2q है।
(iii) यदि a = 3q + 2 है तब
(a)² = (3q + 2)² = 9q² + 12q +4
= 9q² + 12q + 3+ 1
= 3(3q² + 4q + 1) + 1 है
= 3m + 1 …….(iii)
जहाँ m = 3q²+ 4g + 1
अतः उपर्युक्त (i), (ii) एवं (iii) स्थिति से स्पष्ट है कि पूर्णांक a का वर्ग 3m या 3m + 1 के रूप का होता है।

प्रश्न 2.
किसी परेड में 616 सदस्यों वाली एक सेना की टुकड़ी को 32. सदस्यों वाले एक आर्मी बैण्ड के पीछे मार्च करना है। दोनों समूहों को समान संख्या वाले स्तम्भों में मार्च करना है। उन स्तम्भों की अधिकतम संख्या ज्ञात कीजिए।
हल:
616 और 32
यूक्लिड विभाजन एल्गोरिथ्म (विधि) के प्रयोग से-
चरण I: ∵ 616 > 32 अतः यूक्लिड प्रमेयिका के अनुसार
∵ 616 = 32 × 19 + 8
चरण I: ∵ शेषफल 8 ≠ 0 है अतः अब 32 और 8 पर यूक्लिड प्रमेयिका प्रयुक्त करने पर
32 = 8 × 4 + 0
अब शून्य प्राप्त हो जाने पर यह प्रक्रिया समाप्त हो जायेगी। चरण II में भाजक 8 है अतः 616 और 32 का HCF 8 है। इस प्रकार सेना टुकड़ी एवं बैण्ड के सदस्यों का समूह अधिकतम 8 स्तम्भों में मार्च करेंगे।
संक्षेप में इस विभाजन प्रक्रिया को इस प्रकार समझा जा सकता है-

∴ 616 तथा 32 का HCF, 8 है।
इसलिए स्तम्भों की अधिकतम संख्या = 8

प्रश्न 3.
वह सबसे बड़ी संख्या ज्ञात कीजिये जो 245 और 2053 को इस प्रकार विभाजित करती है कि प्रत्येक स्थिति में शेषफल 5 प्राप्त हो।
हल:
यह दिया हुआ है कि 245 और 2053 को अभीष्ट पूर्णांक द्वारा विभाजित (RBSESolutions.com) करने पर प्रत्येक स्थिति में शेषफल 5 रह जाता है। इसलिए 245 -5 = 240 और 2053 – 5 = 2048 को अभीष्ट संख्या द्वारा पूर्णतया विभाजित किया जा सकता है। यह तभी सम्भव है जबकि अभीष्ट संख्या 240 एवं 2048 का उभयनिष्ठ गुणनखण्ड हो। यह भी ज्ञात है कि अभीष्ट संख्या इस उभयनिष्ठ गुणनखण्ड में सबसे बड़ी संख्या है। अर्थात् अभीष्ट संख्या 240 एवं 2048 का  (HCF) होगी। अतः यूक्लिड विभाजन विधि का चरणबद्ध प्रयोग करने पर-
2048 = 240 × 8 + 128
240 = 128 × 1 + 112
128 = 112 ×1 + 16
112 = 16 × 7+ 0
स्पष्ट है कि अन्तिम शेषफल 0 प्राप्त हो गया है। इस प्रकार अभीष्ट महत्तम समापवर्तक भाजक 16 प्राप्त हुआ जो कि अभीष्ट संख्या है।

प्रश्न 4.
दर्शाइये कि \(\sqrt { 2 } +\sqrt { 5 } \) एक अपरिमेय संख्या है।
हल:
माना \(\sqrt { 2 } +\sqrt { 5 } \) एक परिमेय संख्या है।
इसलिए \(\sqrt { 2 } +\sqrt { 5 } =\frac { a }{ b } \), b #0 ……..(i)
जहाँ a, b पूर्णांक सह अभाज्य संख्यायें हैं।
समीकरण (i) को इस तरह से भी लिख सकते हैं

चूँकि a, b पूर्णांक है, अतः \(\frac { { a }^{ 2 }-3{ b }^{ 2 } }{ 2ab } \) एक परिमेय संख्या होगी। अतः समीकरण (ii) से परिणाम प्राप्त होता है कि \(\sqrt { 2 } \) एक परिमेय संख्या है। जबकि हम जानते हैं कि \(\sqrt { 2 } \) एक अपरिमेय संख्या है। अतः यह परिणाम विरोधाभासी है। इसलिए हमारी हमारी परिकल्पना कि \(\sqrt { 2 } +\sqrt { 5 } \) एक परिमेय संख्या है, गलत है।
इससे सिद्ध होता है कि \(\sqrt { 2 } +\sqrt { 5 } \) एक अपरिमेय संख्या है।

प्रश्न 5.
सिद्ध कीजिए कि 2 एक अपरिमेय संख्या है।
हल
माना \(\sqrt { 2 } \) एक परिमेय संख्या है। तब दो पूर्णांक a (RBSESolutions.com)एवं है के लिए निम्न कथन को लिख सकते हैं-
\(\sqrt { 2 } =\frac { a }{ b } ,\quad b\neq 0\)
जहाँ पर a और b सह अभाज्य संख्यायें हैं। अर्थात् a, b में कोई उभयनिष्ठ गुणनखण्ड नहीं है।
अतः \(\sqrt { 2 } \) b = a
दोनों पक्षों का वर्ग करने पर
2b² = a² …..(i)
∵ 2b², 2 से विभाजित होता है, अतः हम कह सकते हैं कि 2, a² को विभाजित करता है।
अतः हम प्रमेय 23 से जानते हैं कि 2, a को भी विभाजित करेगा। इस प्रकार प्रथम परिणाम यह प्राप्त हुआ कि 2, 4 को विभाजित करता है। पूर्णांक 4 को निम्न रूप में लिख सकते हैं
a = 2c जहाँ c एक पूर्णाक है।
अतः a² = 4c² …..(ii)
समीकरण (i) से समीकरण (ii) में a का मान प्रतिस्थापित करने पर हमें निम्न प्राप्त होता है-
2b² = 4c²
अर्थात् b² = 2c²
∵ 2c², 2 से विभाजित होता है अत: b भी 2 से विभाजित होगा।
अतः प्रमेय 2.3 के उपयोग से हम कह सकते हैं कि 2, b को विभाजित करेगा। इस प्रकार द्वितीय परिणाम यह प्राप्त हुआ कि 2, b को भी विभाजित करता है-

प्रथम एवं द्वितीय परिणाम से स्पष्ट है कि 2, पूर्णांक 4 और b का एक उभयनिष्ठ गुणनखण्ड है परन्तु यह कथन प्रारम्भ में प्राप्त तथ्य का विरोधाभासी है। कि a और b में कोई उभयनिष्ठ गुणनखण्ड नहीं है। अतः इससे निष्कर्ष निकलता है कि हमारी शुरू की कल्पना कि \(\sqrt { 2 } \) एक परिमेय संख्या है, गलत है। अतः यह प्रमाणित हुआ कि \(\sqrt { 2 } \) एक अपरिमेय संख्या है।

प्रश्न 6.
सिद्ध कीजिये कि \(\sqrt { 3 } \) एक अपरिमेय संख्या है।
हल:
माना \(\sqrt { 3 } \) एक परिमेय संख्या है। तब दो पूर्णांक a एवं b के लिए निम्न कथन लिखा जा सकता है-
\(\sqrt { 3 } =\frac { a }{ b } ,\quad b\neq 0\)
जहाँ a तथा b सह अभाज्य संख्यायें हैं। अर्थात् a, b में कोई उभयनिष्ठ गुणनखण्ड नहीं है।
अतः \(\sqrt { 3 } \) b = a
दोनों पक्षों का वर्ग करने पर
3b² = a² …..(i)
अतः प्रमेयानुसार यह स्पष्ट है कि 3, 4 को भी विभाजित करेगा। इस प्रकार | प्रथम परिणाम यह प्राप्त होता है कि 3, a को विभाजित करता है। अतः हम पूर्णांक 4 को निम्न रूप में लिख सकते हैं-
a = 3c जहाँ c एक पूर्णाक है।
अतः a² = (3c)² = 9c² …..(ii)
समीकरण (i) तथा (ii) से
3b² = 9c² अर्थात् b² = 3c²
यहाँ चूंकि 3c²,3 से विभाजित होता है, अत: b भी 3 से विभाजित होगा।
अतः प्रमेयानुसार हम कह सकते हैं कि 3, b को विभाजित करेगा। इस प्रकार (RBSESolutions.com) द्वितीय परिणाम यह प्राप्त हुआ कि 3, b को विभाजित करता है।
समीकरण (i) एवं (ii) परिणामों से स्पष्ट है कि 3, पूर्णांक a और b का एक उभयनिष्ठ गुणनखण्ड है लेकिन यह कथन प्रारम्भ में प्राप्त तथ्य को विरोधाभासी है कि a और b में कोई उभयनिष्ठ गुणनखण्ड नहीं है। अतः निष्कर्ष निकलता है कि हमारी प्रारम्भिक कल्पना कि \(\sqrt { 3 } \) एक परिमेय संख्या है, गलत है।
अत: यह सिद्ध हुआ कि \(\sqrt { 3 } \) एक अपरिमेय संख्या है।

प्रश्न 7.
सिद्ध कीजिये कि \(\sqrt { 5 } \) एक अपरिमेय संख्या है।
हल:
माना \(\sqrt { 5 } \) एक परिमेय संख्या है। तब दो पूर्णांकों a और b के लिए निम्न कथन लिखा जा सकता है कि
\(\sqrt { 5 } =\frac { a }{ b } ,\quad b\neq 0\)
जहाँ a और b सह अभाज्य (co-prime) संख्याएँ हैं अर्थात् a, b में कोई उभयनिष्ठ गुणनखण्ड नहीं है।
अतः \(\sqrt { 5 } \)b = a
⇒ 5b² = a² ……..(i)
चूँकि 5b², 5 से विभाजित होता है अतः a² भी 5 से विभाजित किया जा सकता है।
प्रमेयानुसार हम कह सकते हैं कि 5, a को भी विभाजित करेगा। इस प्रकार | प्रथम परिणाम यह प्राप्त हुआ है कि 5, a को विभाजित करता है। अतः पूर्णांक 4 को निम्न रूप में लिख सकते हैं
a = 5c, जहाँ c एक पूर्णाक है।
⇒ a² = 25c² …..(ii)
समीकरण (i) एवं (ii) से हमें निम्न प्राप्त होता है-
5b² = 25c²
⇒ b² = 5c²
यहाँ स्पष्ट है कि 2, 5 से विभाजित किया जा सकता है।
प्रमेयानुसार 5, b को भी विभाजित करेगा। इस प्रकार द्वितीय परिणाम यह प्राप्त हुआ कि 5, b को विभाजित करता है।
समीकरण (i) तथा (ii) से कि 5, पूर्णांक a और B का एक उभयनिष्ठ गुणनखण्ड है परन्तु यह कथन प्रारम्भ में प्राप्त तथ्य का विरोधाभासी है कि a और b में कोई उभयनिष्ठ गुणनखण्ड नहीं है।
अतः निष्कर्ष निकलता है कि हमारी प्रारम्भिक कल्पना कि 5 एक परिमेय संख्या है, गलत है।
अतः यह प्रमाणित होता है कि \(\sqrt { 5 } \) एक अपरिमेय संख्या है।

प्रश्न 8.
दर्शाइये कि किसी धनात्मक पूर्णाकं का घन, (RBSESolutions.com) किसी पूर्णांक m के लिये 4m, 4m + 1 या 4m + 3 के रूप का होता है।
हल:
माना कि एक घन पूर्णाक है।
यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग करने पर यह 4q या 4q + 1 या 4q + 2 या 4q + 3 के रूप का होगा।
अतः इसकी निम्नलिखित स्थितियाँ उत्पन्न होंगी-
स्थिति I. जब x = 4q
तब दोनों पक्षों का धन करने पर
(x)³ = (4q)³ = 64q³
= 4 × (16q³)
= 4m, जहाँ m = 16q²³

स्थिति II. जब x = 4q + 1
⇒ तब (x)³ = (4q + 1)³ दोनों पक्षों का धन करने पर
⇒x³ = 64q³ + 48q² + 12q + 1
= 4q(16q² + 12q + 3) + 1
= 4m + 1, जहाँ m = q(16q² + 12q + 3)

स्थिति III. जब x = 4q + 2
⇒ तब x³ = (4q + 2)³ दोनों पक्षों (RBSESolutions.com) को धन करने पर
⇒ x³ = 6q³ + 96q² + 48q + 8
= 4(16q³ + 24q² + 12q + 2)
= 4m, जहाँ m = 16q³ + 24q² + 12q + 2

स्थिति IV. जबे x = 4q + 3
⇒ तब x³ = (4q + 3)³ दोनों पक्षों का धन करने पर
⇒ x³ = 64q³ + 144q² + 108q + 27
= 64q³ + 144q² + 108q + 24 + 3
= 4(16q³ + 36q² + 27q + 6) + 3
= 4m + 3, जहाँ m = 16q² + 36q + 27q + 6
अतः किसी धनात्मक पूर्णांक का धन, किसी पूर्णांक m के लिये 4m, 4m + 1 या 4m + 3 के रूप का होता है । ( इतिसिद्धम् )

We hope the RBSE Solutions for Class 10 Maths Chapter 2 वास्तविक संख्याएँ Additional Questions help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 2 वास्तविक संख्याएँ Additional Questions, drop a comment below and we will get back to you at the earliest.