RBSE Solutions for Class 10 Maths Chapter 2 वास्तविक संख्याएँ Ex 2.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 2 वास्तविक संख्याएँ Exercise 2.2.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Chapter Name | वास्तविक संख्याएँ |
| Exercise | Exercise 2.2 |
| Number of Questions Solved | 5 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 2 वास्तविक संख्याएँ Ex 2.2
प्रश्न 1.
अग्रलिखित संख्याओं को अभाज्य गुणनखण्डों के (RBSESolutions.com) गुणनफल के रूप में व्यक्त कीजिए–
(i) 468
(ii) 945
(iii) 140
(iv) 3825
(v) 20570
हल:
(i) 468 के अभाज्य गुणनखण्ड
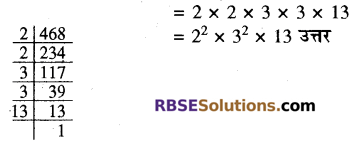
(ii) 945 के अभाज्य गुणनखण्ड
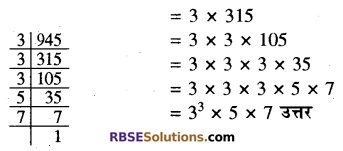
(iii) 140 के अभाज्य गुणनखण्ड
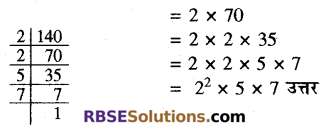
(iv) 3825 के अभाज्य गुणनखण्ड
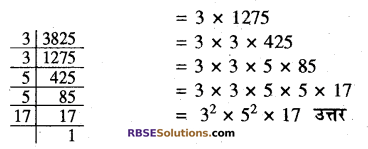
(v) 20570 के अभाज्य गुणनखण्ड
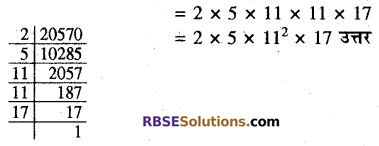
प्रश्न 2.
पूर्णांकों के निम्नलिखित युग्मों का महत्तम समापवर्तक (HCF) एवं लघुत्तम (RBSESolutions.com) समापवर्तक (LCM) ज्ञात कीजिए तथा सत्यापित कीजिए कि HCF x LCM = पूर्णाकों का गुणनफल
(i) 96 और 404
(ii) 336 और 54
(iii) 90 और 144
हल:
(i) 96 और 404
96 के अभाज्य गुणनखण्ड, = 2 × 48
= 2 × 2 × 24
= 2 × 2 × 2 × 2 × 2 × 3
= 25 × 3
404 के अभाज्य गुणनखण्ड = 2 × 202
= 2 × 2 × 101
= 22 × 101
इसलिए 96 और 404 को LCM = 25 × 3 × 101
L.C.M, के लिये अभाज्य गुणनखण्ड (RBSESolutions.com) की अधिकतम घात लेने पर
= 32 × 3 × 101
= 96 × 101 = 9696 उत्तर
तथा 96 और 404 का HCF = 22 = 2 x 2 = 4 उत्तर
H.C.F के लिए उभयनिष्ठ अभाज्य गुणनखण्ड की न्यूनतम घात लेने पर
सत्यापन-HCF (96, 404) × LCM (96, 404)
= 4 × 25 × 3 × 101
= (4 × 101) × 32 × 3
= 404 × 96 = 96 × 404
= दी गई संख्याओं का गुणनफल
![]()
(ii) 336 और 54
336 के अभाज्य गुणनखण्ड = 2 × 168
= 2 × 2 × 84
= 2 × 2 × 2 × 42
= 2 × 2 × 2 × 2 × 21
= 2 × 2 × 2 × 2 × 3 × 7
= 24 × 3 × 7
54 के अभाज्य गुणनखण्ड = 2 × 27
2 × 3 × 9
= 2 × 3 × 3 × 3
= 2 × 33
H.C.F के लिये उभयनिष्ठ अभाज्य गुणनखण्ड (RBSESolutions.com) की न्यूनतम घात लेने पर
∴ HCF (336, 54) = 2 × 3 = 6 उत्तर L.C.M, के लिये अभाज्य गुणनखण्ड की अधिकतम घात लेने पर।
LCM = 24 × 33 × 7 = 16 × 27 × 7
= 3024 उत्तर
सत्यापन-HCF (336, 54) × LCM (336, 54)
= 6 × 3024
= 2 × 3 × 24 × 33 × 7
= 24 × 3 × 7 × 2 × 33
= 336 x 54
= दी गई संख्याओं का गुणनफल
(iii) 90 और 144
90 के अभाज्य गुणनखण्ड = 2 × 45
= 2 × 3 × 15
= 2 × 3 × 3 × 5
= 2 × 32 × 5
144 के अभाज्य गुणनखण्ड = 2 × 72
= 2 × 2 × 36
= 2 × 2 × 2 × 18
= 2 × 2 × 2 × 2 × 9
= 2 × 2 × 2 × 2 × 3 × 3
= 24 × 32
H.C.F के लिये उभयनिष्ठ अभाज्य गुणनखण्ड (RBSESolutions.com) की न्यूनतम घात लेने पर
∴ HCF (90, 144) = 2 × 32 = 2 × 9 = 18 उत्तर
L.C.M. के लिये अभाज्य गुणनखण्ड की अधिकतम घात लेने पर
LCM (90, 144) = 24 × 32 × 5
= 16 x 9 x 5 = 720 उत्तर
सत्यापन-HCF (90, 144) × LCM (90, 144)
= 18 × 16 × 9 × 5
= 18 × 5 × 16 × 9
= 90 × 144
= दी गई संख्याओं का गुणनफल
![]()
प्रश्न 3.
अभाज्य गुणनखण्डन विधि द्वारा निम्नलिखित पूर्णाकों (RBSESolutions.com) का महत्तम समापवर्तक एवं लघुत्तम समापवर्तक ज्ञात कीजिए
(i) 12, 15 और 21
(ii) 24, 15 और 36
(iii) 17, 23 और 29
(iv) 6, 12 और 120
(v) 40, 36 और 126
(v) 8, 9 और 25
हल:
(i) 12, 15 और 21
12 के अभाज्य गुणनखण्ड = 2 × 2 × 3
15 के अभाज्य गुणनखण्ड = 3 × 5
21 के अभाज्य गुणनखण्ड = 3 × 7
L.C.M. के लिये अभाज्य गुणनखण्ड की अधिकतम घात लेने पर
∴ LCM (12, 15 और 21) = 22 × 3 × 5 × 7
= 420 उत्तर
H.C.F के लिये उभयनिष्ठ अभाज्य गुणनखण्ड की न्यूनतम घात लेने पर।
तथा HCF (12, 15 और 21) = 3 उत्तर
![]()
(ii) 24, 15 और 36
24 के अभाज्य गुणनखण्ड = 2 × 2 × 2 × 3
= 22 × 3
15 के अभाज्य गुणनखण्ड = 3 × 5
36 के अभाज्य गुणनखण्ड = 2 × 2 × 3 × 3
= 22 × 32
L.C.M, के लिये अभाज्य गुणनखण्ड की अधिकतम घात लेने पर
∴ LCM (24, 15 और 36) = 22 × 32 × 5
= 8 × 9 × 5
= 360 उत्तर
H.C.F के लिये उभयनिष्ठ अभाज्य गुणनखण्ड (RBSESolutions.com) की न्यूनतम घात लेने पर तथा HCF (24, 15 और 36) = 3 उत्तर
(iii) 17, 23 और 29
17 के अभाज्य गुणनखण्ड = 1 × 17
23 के अभाज्य गुणनखण्ड = 1 × 23
29 के अभाज्य गुणनखण्ड = 1 × 29
L.C.M, के लिये अभाज्य गुणनखण्ड की अधिकतम घात लेने पर
∴ LCM (17, 23 और 29) = 17 × 23 × 29
= 11339 उत्तर
H.C.F के लिये उभयनिष्ठ अभाज्य गुणनखण्ड की न्यूनतम घात लेने पर
तथा HCF (17, 23 और 29) = 1 उत्तर
(iv) 6, 72 और 120
6 के अभाज्य गुणनखण्ड = 2 × 3
72 के अभाज्य गुणनखण्ड = 2 × 2 × 2 × 3 × 3
= 23 × 32
120 के अभाज्य गुणनखण्ड = 2 × 2 × 2 × 3 × 5
=23 × 3 × 5
L.C.M, के लिये अभाज्य गुणनखण्ड की अधिकतम घात लेने पर
∴ LCM (6, 72 और 120) = 2 × 3 × 5
= 8 × 9 × 5
= 360 उत्तर
H.C.F के लिये उभयनिष्ठ अभाज्य गुणनखण्ड की न्यूनतम घात लेने पर तथा HCF (6, 72 और 120) = 2 x 3
= 6 उत्तर
![]()
(v) 40, 36 और 126
40 के अभाज्य गुणनखण्ड = 2 × 2 × 2 × 5
= 23 × 5
36 के अभाज्य गुणनखण्ड = 2 × 2 × 3 × 3
= 22 × 32
126 के अभाज्य गुणनखण्ड = 2 × 3 × 3 × 7
= 23 × 32 × 7
L.C.M, के लिये अभाज्य गुणनखण्ड की अधिकतम घात लेने पर
∴ LCM (40, 36 और 126) = 23 × 32 × 5 × 7
= 8 × 9 × 5 × 7
= 2520 उत्तर
H.C.F के लिये उभयनिष्ठ अभाज्य गुणनखण्ड (RBSESolutions.com) की न्यूनतम घात लेने पर
तथा HCF (40, 36 और 126) = 2 उत्तर
(vi) 8, 9 और 25
8 के अभाज्य गुणनखण्ड = 2 × 2 × 2 = (2)3 x 1
9 के अभाज्य गुणनखण्ड = 3 × 3 = (3)2 × 1
25 के अभाज्य गुणनखण्ड = 5 × 5 = (5)2 x 1
L.C.M, के लिये अभाज्य गुणनखण्ड की अधिकतम घात लेने पर
∴ LCM (8, 9 और 25) = (2)3 × (3)2 × (5)2
= 8 × 9 × 25
= 1800 उत्तर
H.C.F के लिये उभयनिष्ठ अभाज्य गुणनखण्ड की न्यूनतम घात लेने पर
तथा HCF (8, 9 और 25) = 1 उत्तर
![]()
प्रश्न 4.
किसी खेल के मैदान के वृत्ताकार पथ पर मैदान का (RBSESolutions.com) एक चक्कर पूरा करने में रमन को 18 मिनट लगते हैं, जबकि इसी वृत्ताकार पथ पर मैदान का एक चक्कर पूरा करने में अनुप्रिया को 12 मिनट का समय लगता है। माना कि दोनों एक ही स्थान से एक ही समय पर चलना प्रारम्भ करते हैं तथा एक ही दिशा में चलते हैं तो बताइये कितने समय बाद दोनों पुनः प्रारम्भिक स्थान पर मिलेंगे?
हल:
रमन द्वारा वृत्ताकार मैदान का 1 चक्कर लगाने का समय = 18 मिनट अनुप्रिया द्वारा उसी मैदान का एक चक्कर लगाने में लगा समय = 12 मिनट
यह ज्ञात करने के लिए कि वे पुनः दोनों कितने समय के बाद प्रारम्भिक बिन्दु पर मिलेंगे, हमें 18 वे 12 का LCM ज्ञात करना होगा।
अतः 18 के अभाज्य गुणनखण्डन = 2 × 9
= 2 × 3 × 3 = 2 × 32
तथा 12 के अभाज्य गुणनखण्डन = 2 × 6
= 2 × 2 × 3 = 22 × 3
18 और 12 के सभी अधिकतम घातांक में अभाज्य (RBSESolutions.com) गुणनखण्डों का गुणनफल लेने पर
∴ LCM (18, 12) = 22 × 32
= 4 × 9 = 36
अर्थात् रमन एवं अनुप्रिया प्रारम्भिक बिन्दु पर 36 मिनट बाद मिलेंगे। उत्तर
प्रश्न 5.
एक संगोष्ठी में हिन्दी, अंग्रेजी तथा गणित में भाग लेने वाले प्रतिभागियों की संख्या क्रमशः 60, 84 और 108 है। यदि प्रत्येक कमरे में बराबर संख्या में एक ही विषय के प्रतिभागी बैठाये जाते हैं तो आवश्यक कमरों की न्यूनतम संख्या ज्ञात कीजिए।
हल:
चूँकि न्यूनतम कमरों की आवश्यकता है। इसलिये प्रत्येक (RBSESolutions.com) कमरे में प्रत्याशियों की संख्या 60, 84 और 108 का H.C.F होगा
60 के अभाज्य गुणनखण्ड = 2 × 2 × 3 × 5
= 22 × 3 × 5
84 के अभाज्य गुणनखण्ड = 2 × 2 × 3 × 7
= 22 x 3 x 7
108 के अभाज्य गुणनखण्ड = 2 × 2 × 3 × 3 × 3
= 22 × 33
हमें प्रत्येक कमरे में बराबर संख्या में प्रतिभागी बैठाने हैं। अत: HCF निकालने पर
HCF = 22 × 3 = 4 x 3 = 12
अतः प्रत्येक कमरे में 12 प्रत्याशियों को बैठाया जा सकता है।
![]()

अतः अभीष्ट कमरों की संख्या 21 है। उत्तर
We hope the RBSE Solutions for Class 10 Maths Chapter 2 वास्तविक संख्याएँ Ex 2.2 help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 2 वास्तविक संख्याएँ Exercise 2.2, drop a comment below and we will get back to you at the earliest.