RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Miscellaneous Exercise

Rajasthan Board RBSE Class 11 Maths Chapter 2 Relations and Functions Miscellaneous Exercise

Question 1.
If A = {a, b, c, d} and B = {p, q, r, s} then relation from A to B is
(A) {(a, p), (b, s, (c, r)}
(B) {(a, p), (b, q), (c, r), (s, d)}
(C) {{b, a), (q, b), (c, r)}
(D) {(c, s), (d, s), (r, a), (q, b)}
Solution:
A × B = {(a, p), (a, q), (a, r), (a, s), {b, p), (b, q), {b, r), (b, s), (c, p), (c, q), (c, r) (c, s) (d, p), (d, q), (d, r), (d, s)}
{(a, p), (b, r), (c, r)}
Because {(a, p), (b, r), (c, r)} ⊆ A × B.
Hence, option (A) is correct.

Question 2.
A relation R in N is defined such that xRy ⇔ x + 4y = 16, then the range of R is
(A) {1, 2, 4}
(B) {1, 3, 4}
(C) {1, 2, 3}
(D) {2, 3, 4}
Solution:
Given,set N = set of natural number = {1, 2, 3,…}
A relation R in Nto N is defined as
xRy ⇔ x + 4y = 16 ∀ x, y ∈ N
or xRy ⇔ y = \(\frac { 16-x }{ 2 }\) ∀ x, y ∈ N
when x = 4 then

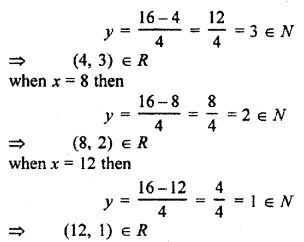
So, R = {(4, 3), (8, 2), (12, 1)}
So, range of R= {3, 2, 1} and {1, 2, 3}
Hence, option (C) is correct.

Question 3.
Rule form of relation {(1, 2), (2, 5), (3, 10), (4, 17), …} in N
(A) {(x, y) : x, y ∈ N, y = 2x + 1}
(B) {(x, y) : x, y ∈ N, y = x² + 1}
(C) {(x, y) : x, y ∈ N, y = 3x – 1}
(D) {(x, y) : x, y ∈ N, y = x + 3}
Solution:
{(x, y) : x, y ∈ N, y = x² + 1}
when x = 1, then y = (1)² + 1 = 2 ⇒ (1, 2) ∈ N
when x = 2, then y = (2)² + 1 = 4 + 1 = 5 ⇒ (2, 5) ∈ N
when x = 3, then y = (3)² + 1 = 9 + 1 = 10 ⇒ (3, 10) ∈ N
when x = 4, then y = (4)² + 1 = 16 + 1 = 17 ⇒ (4, 17) ∈ N
So, R = {(1, 2), (2, 5), (3, 10), (4, 17), …}
= {(x, y) : x, y ∈ N, y = x² + 1}
Hence, option (B) is correct.

Question 4.
If A = {2, 3, 4} and B = {3, 4, 5, 6, 7, 8} : A relation if from A to B is defined such that “x divides y” then R^-1 is
(A) {(4, 2), (6, 2), (8, 2), (3, 3), (6,3), (4, 4), (8, 4)}
(B) {(2, 4), (2, 6), (2, 8), (3, 3), (3, 6), (4, 4), (4, 8)}
(C) {(3, 3), (4, 4), (8, 4)}
(D) {(4, 2), (6, 3), (8, 4)}
Solution:
Given sets are
A = {2, 3, 4} and B = {3, 4, 5, 6, 7, 8}
Relation R from A to B is defined as
“x divides y” ∀ x ∈ A, y ∈ B
So, when x = 2 ∈ A
Then 2 divides the element 4, 6, 8 of B.
So, (2, 4), (2, 6), (2, 8) ∈ R
when x = 3 ∈ A, then 3 divides elements 3, 6 of B
So, (3, 3), (3, 6) ∈ R
when x = 4 ∈ A then 4 divides the elements 4, 8 of B.
So, (4, 4), (4, 8) ∈ R
R = {(2, 4), (2, 6), (2, 8), (3, 3), (3, 6), (4, 4), (4, 8)}
R^-1 = {(4, 2), (6, 2), (8, 2), (3, 3), (6, 3), (4, 4), (8, 4)}
Hence, option (A) is correct.

Question 5.
In the set of real numbers, Relation “x is smaller than y” will be
(A) Reflexive and Transitive
(B) Symmetric and Transitive
(C) Anti-symmetric and Transitive
(D) Reflexive and Anti-symmetric
Solution:
Because this relationship is only transitive
If “x is less than or equal to y” then this relation is reflexive and anti-symmetric.
Hence, option (C) is correct.

Question 6.
A relation R inset of non zero integers is defined as xRy ⇔ xy = yx then R is
(A) reflexive and symmetric but not transitive
(B) reflexive and anti-symmetric but not transitive
(C) reflexive, anti-symmetric and transitive
(D) reflexive, symmetric and transitive
Solution:
Given, Set I₀ = set of non-zero integers = {±1, ±2, …}
A relation in I₀xRy ⇔ xy = yx ∀ x, y ∈ I₀
⇔ y log x = x log y ∀ x, y ∈ I₀
To prove R is equivalence relation we have to prove that R is reflexive, symmetric and transitive relation.
(i) Reflexivity: Let a ∈ I₀
a ∈ I₀
⇒ a log a = a log a ∀ a ∈ I₀
R is reflexive.

(ii) Symmetricity: Let a, b ∈ I₀
Now, (a, b) ∈ R
(a, b) ∈ R
⇒ b log a = a log b
⇒ (b, a) ∈ R
So, (a, b) ∈ R
⇒ (b, a) ∈ R ∀ a, b ∈ I₀
R is a symmetric relation.

(iii) Transitivity: Let a, b, c ∈ I₀
Now, (a, b) ∈ R, (b, c) ∈ R
(a, b) ∈ R ⇒ b log a = a log b ……(1)
(b, c) ∈ R ⇒ c log b = b log c
⇒ b log c = c log b …(2)
By dividing equation (1) from equation (2).

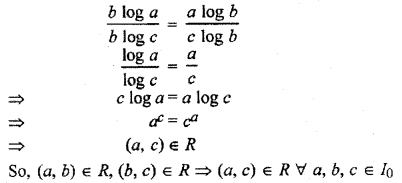
R is a transitive relation.
Thus, it is proved that R is reflexive, symmetric and transitive relation.
Hence, the option (D) is correct.

Question 7.
If relation R is defined as “x is divisor of y” then from the following subet of N. Which is a total ordered set ?
(A) {36, 3, 9}
(B) {7, 77, 11}
(C) {3, 6, 9, 12, 24}
(D) {1, 2, 3, 4, …}
Solution:
Given : N = set of natural numbers = (1, 2, 3, 4, …}
A relation R is N is defined as
xRy ⇒ “x is divisor of y” ∀ x, y ∈ N
⇒ \(\frac { y }{ x }\) = k ∈ N
where N is a set of natural numbers ∀ x, y ∈ N
From option ‘A’, \(\frac { 36 }{ 9 }\), \(\frac { 36 }{ 3 }\), \(\frac { 9 }{ 3 }\) all are natural numbers
From option ‘B’, \(\frac { 11 }{ 7 }\) ∉ N, from option ‘C’, \(\frac { 9 }{ 6 }\) ∉ N
From option ‘D’, \(\frac { 3 }{ 2 }\) ∉ N, Hence, option (A) is correct.

Question 8.
From the following relations defined on set Z of integers, which of the relation is not equivalence relation
(A) aR₁b ⇔ (a + b) is an even integer
(B) aR₂b ⇔ (a – b) is an even integer
(C) aR₃b ⇔ a < b
(D) aR₄b ⇔ a = b
Solution:
Correct option (C)
aR₃b ⇔ a < b, R₃ is not an equivalence relation because it is not reflexive and symmetric.
Hence, option (C) is correct.

Question 9.
A relation R is defined on set A = {1, 2, 3}, where R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)}, then R is
(A) reflexive but not transitive
(B) reflexive but not symmetric
(C) symmetric and transitive
(D) neither symmetric nor reflexive
Sotution:
Given : Set A = {1, 2, 3} and R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)}
(i) Reflexivity: (1, 1) ∈ R, (2, 2) ∈ R, (3, 3) ∈ R
(a, a) ∈ R
R is reflexive.

(ii) Symmetricity: (1, 2) = (2, 1) ∉ R
(1, 3) = (3, 1 ) ∉ R
(2, 3) = (3, 2) ∉ R
(a, b) ∈ R ⇒ (b, a) ∉ R So, R is not symmetric
Hence, option (B) is correct.

Question 10.
If A = {a, b, c}, then number of possible non-zero relations in A is
(A) 511
(B) 512
(C) 8
(D) 7
Solution:
A = {a, b, c} Number of elements in A = n(A) = 3
Then, numbers of elements in A × A = n(A × A) = 3² = 9
So, the number of relations in A are = 2ⁿ – 1 = 2⁹ – 1 = 512 – 1 = 511.
Hence, option (A) is correct.

Question 11.
If A = {1, 2, 3, 4} then which of the following is a function in A
(A) f₁ = {(x, y) : y = x + 1}
(B) f₂ = {(x, y) : x + y > 4}
(C) f₃ = {(x, y) : y < x}
(D) f₄ = {(x, y) : x + y = 5}
Solution:
Here, f₁ = {(x, y) : y = x + 1} = {(1, 2), (2, 3), (3, 4)}
f₂ = {(x, y) : x + y > 4} = (1, 4), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)}
f₃ = {(x, y) : y < x} = {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)}
f₄ = {(x, y) : x + y = 5} = {(x, y) : x = 5 – y} = {(1, 4), (2, 3), (3, 3), (4, 1)}
It is clear that only f₄ is a function because eveiy element of A corresponts to unique element in B.
Hence, the option (D) is correct.

Question 12.
Function f : N → N, f(x) = 2x + 3 is
(A) One-one onto
(B) One-one into
(C) Many one-onto
(D) Many-one into
Solution:
Given: f : N → N and f(x) = 2x + 3
where N = set of natural numbers
Let x₁, x₂ ∈ N is such that f(x₁) = f(x₂)
f(x₁) = f(x₂)
⇒ 2x₁ + 3 = 2x₂ + 3
⇒ 2x₁ = 2x₂
⇒ x₁ = x₂
f(x₁) = f(x₂) ⇒ x₁ = x₂ ∀ x₁, x₂ ∈ N
f is one-one function.
Again, let y ∈ N (co-domain) if possible than let pre image of x is in domain N then f(x) = y
f(x) = y
⇒ 2x + 3 = y
⇒ x = \(\frac { y-3 }{ 2 }\) ∈ N
At y = 1, then x = \(\frac { 1-3 }{ 2 }\) = -1 ∉ N
If this way, y has many values for which x is not exist in domain A. So, f is into function.
Hence, option (B) is correct.

Question 13.
Which one of the following is onto function define from R to R.
(A) f(x) = |x|
(B) f(x) = e^-x
(C) f(x) = x³
(D) f(x) = sin x
Solution:
f(x) = x³
Given, f : R → R and f(x) = x³
Let y ∈ R (co-domain) if possible, then let pre-image of y is x in domain R, then
f(x) = y
⇒ x³ = y
⇒ x = y^1/3 ∈ R ∀ y ∈ R
So, pre-image of each value ofy is exist in domain R.
So, R is onto function.
Hence, option (C) is correct.

Question 14.
Which of the following is one-one function defined from R to R
(A) f(x) = |x|
(B) f(x) = cos x
(C) f(x) = e^x
(D) f(x) = x²
Solution:
(C) f(x) = e^x
Let x, y ∈ R are such that
f(x) = f(y)
⇒ e^x = e^y
⇒ x log_e e = y log_e e
⇒ x = y
f(x) = f(y)
⇒ x = y [∵ log_e e = 1]
f is one-one function ∀ x, y ∈ R

Question 15.
f : R → R, f(x) = x² + x is:
(A) One-one one
(B) One-one into
(C) Many-one onto
(D) Many one onto
Solution:
Given: f : R → R and f(x) = x² + x
where R is a set of real numbers.
Let x₁, x₂ ∈ R are such that f(x₁) = f(x₂)
f(x₁) = f(x₂)
⇒ x₁² + x₁ = x₂² + x₂
⇒ x₁² – x₂² + x₁ – x₂ = 0
⇒ (x₁ – x₂)(x₁ + x₂) + 1 (x₁ – x₂) = 0
⇒ (x₁ – x₂) (x₁ + x₂ + 1} = 0
⇒ x₁ = x₂, x₁ = -(x₂ + 1) ∀ x₁, x₂ ∈ R
Here, element of set A relates to two elements of set B.
So, it is a many-one function.
Again, let y ∈ R (co-domain)
If possible then let pre-image of y is x in domain R.
then f(x) = y
⇒ x² + x = y
⇒ x(x + 1) = y
⇒ x = y, x = y – 1
If y < 1, then there is no real value of x.
So, pre-image of many elements of R does not exist in domain R, so, f is an into function.
Thus, f is many-one, into function.
Hence, the option (D) is correct.

Question 16.
Which of the following is onto function—
(A) f : Z → Z, f(x) = |x|
(B) f : N → Z, f(x) = |x|
(C) f : R₀ → R⁺, f(x) = |x|
(D) f : C → R, f(x) = |x|
Solution:
f : R₀ → R⁺, f(x) = |x|
Pre-image of every positive real number is exists in domain R₀. So, function is onto.
Hence, option (C) is correct.

Question 17.
Domain of function
\(f(x)=\frac { 1 }{ \sqrt { \left| x \right| -x } }\)
(A) R⁺
(B) R^–
(C) R₀
(D) R
Solution:

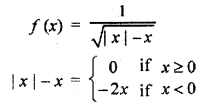
It is clear that function is defined is x < 0 because [x ≥ 0 then f(x) = ∞]
Required domain of f(y) = R^–
Hence, option (B) is correct.

Question 18.
If x is real number than the range of

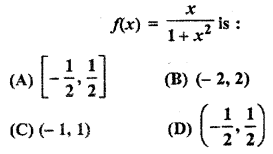
Solution:

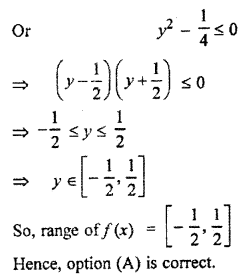
Question 19.
Range of function f(x) = \(\cos { \frac { x }{ 3 } }\) is
(A) (0, ∞)
(B) (\(\frac { -1 }{ 3 }\), \(\frac { 1 }{ 3 }\))
(C) [-1, 1]
(D) [0, 1]
Solution:
Let y = \(\cos { \frac { x }{ 3 } }\)
-1 ≤ \(\cos { \frac { x }{ 3 } }\) ≤ 1
-1 ≤ y ≤ 1
x is defined if -1 ≤ y ≤ 1
Hence, required range = [-1, 1]
Hence, option (C) is correct.

Question 20.
From ]\(\frac { -\pi }{ 2 } ,\frac { -\pi }{ 2 }\)[ which of the following is one-one onto function defined in R
(A) f(x) = tan x
(B) f(x) = sin x
(C) f(x) = cos x
(D) f(x) = e^x + e^-x
Solution:
f(x) = tan x

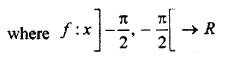
Hence, option (A) is correct.

Question 21.
Find the domain and range of the relaton R
R = {(x + 1, x + 5)} : x ∈ {0, 1, 2, 3, 4, 5}
Solution:
Given relation
R = {(x + 1, x + 5) : x ∈ (0, 1, 2, 3, 4, 5}
Then, domain of relation R {(x + 1) : x ∈ {0, 1, 2, 3, 4, 5}
Domain of R = {1, 2, 3, 4, 5, 6}
and Range of R = {(x + 5) : x ∈ (0, 1, 2, 3, 4, 5}
Range of R = {5, 6, 7, 8, 9, 10}

Question 22.
If A = {1, 2}, then write all non-zero relations defined in A.
Solution:
All non-zero relation are:
{(1, 1)}, {(2, 2)}, {(1, 2)}, {(2, 1)}
{(1, 1), (1, 2)}, {(1, 1), (2, 1)}, {(2, 2), (1,2)}, {(2, 2), (2, 1)}, {(1, 2), (2, 1)}
{(1, 1), (2, 2), (1, 2)}, {(1, 1), (2, 2), (2, 1)}, {(1, 1), (1, 2), (2, 1)}, {(2, 2), (1, 2), (2, 1)}
{(1, 1), (1, 2), (2, 1), (2, 2)}

Question 23.
Find the domain and range of the following relations
(i) R₁ = {(x, y) : x, y ∈ N, x + y = 10}
(ii) R₂ = {(x, y) : y = |x – 1|, x ∈ z and |x| ≤ 3}
Solution:
(i) Given set N = {1, 2, 3,…}
A relation R₁ in N is defined as
R₁ = {(x, y) : x, y ∈ N, x + y = 10} ∀ x, y ∈ N
So, xR₁y ⇔ x + y = 10 ⇔ y = 10 – x
when x = 1, then y = 10 – 1 = 9 ∈ N then (1, 9) ∈ R₁
when x = 2, then y = 10 – 2 = 8 ∈ N then (2, 8) ∈ N
when x = 3, then y = 10 – 3 = 7 ∈ N then (3, 7) ∈ R₁
when x = 4, then y = 10 – 4 = 6 ∈ N then (4, 6) ∈ R₁
Similarly, (5, 5) ∈ R₁, (6, 4) ∈ R₁, (7, 3) ∈ R₁, (8, 2) ∈ R₁, (9, 1) ∈ R₁
R₁ = {(1, 9), (2, 8), (3, 7), (4, 6), (5, 5), (6, 4), (7, 3), (8, 2), (9, 1)}
Domain of R₁ ={1, 2, 3, 4, 5, 6, 7, 8, 9}
Range of R₁ = {9, 8, 7, 6, 5, 4, 3, 2, 1}

(ii) Given set Z = set of integers = {0, ±1, ±2, ±3,…}
A relation R in Z is defined as
R₂ = {(x, y), y = |x – 1|, x ∈ z and x ≤ 3}
or xRy ⇔ y = |x – 1|, |x| ≤ 3 ∀ y ∈ Z
Here |x| ≤ 3 ⇒ -3 ≤ x ≤ 3, x ∈ Z

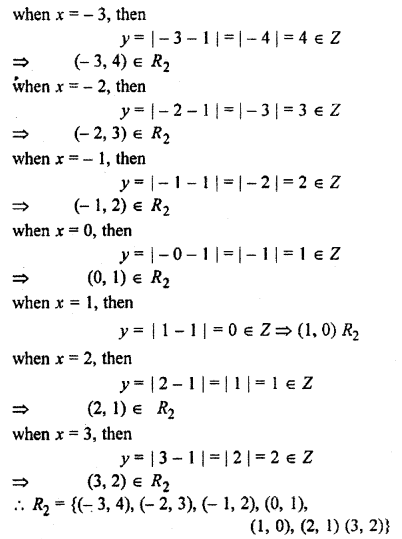
Domain of R₂ = {-3, -2, -1, 0, 1, 2, 3}
Range of R₂ = {4, 3, 2, 1, 0}

Question 24.
In the set of real numbers R, two relations R₁ and R₂ can be defined as
(i) aR₁b ⇔ a – b > 0
(ii) aR₂b ⇔ |a| ≤ b
Also test the reflexivity, symmetricity and transitivity of R₁ and R₂.
Solution:
(i) Given set R = Set of real numbers
Reflexivity R aR₁b ⇔ a – b > 0 ∀ a, b ∈ R
Reflexivity : Let a ∈ R
a ∈ R
⇒ a – a = 0 > 0
⇒ a – a \(\ngtr \) 0
⇒ (a, a) ∉ R₁ a ∈ R
R is not reflexive relation.
Symmetricity : Let a, b ∈ R are such that (a, b) ∈ R₁
(a, b) ∈ R₁
⇒ a – b > 0
⇒ b – a < 0
⇒ (b, a) ∉ R₁
So, (a, b) ∈ R₁
⇒ (b, a) ∉ R₁
R₁ is not symmetric.
Transitivity : Let a, b, c ∈ R are such that
(a, b) ∈ R₁, (b, c) ∈ R₁
(a, b) ∈ R₁
⇒ a – b > 0 …(1)
(b, c) ∈ R₁ ⇒ b – c > 0 …(2)
and a – c = (a – b) + (b – c) > 0 [∴ From (1) and (2)]
⇒ a – c > 0
⇒ (a, c) ∈ R₁
So, (a, b) ∈ R₁, (b, c) ∈ R₁
⇒ (a, c) ∈ R₁ ∀ a, b, c ∈ R
R₁ is transitive.
From above it is clear that R₁ is not reflexive and symmetric relation.
It is only a transitive relation.

(ii) Given: Relation R = set of real numbers
A relation R₂ in R is defined as
aR₂b ⇔ |a| ≤ b ∀ a, b ∈ R
Reflexivity: Let a ∈ R
a ∈ R ⇒ |a| ≤ a is not necessary
For example a = -2 ∈ R
and |-2| ≤ -2 ⇒ (-2, -2) ∈ R₂
So, R₂ is not a reflexive relation.
Symmetricity: Let (a, b) ∈ R are such that (a, b) ∈ R₂
(a, b) ∈ R₂ ⇒ |a| ≤ b
Then |b| ≤ a is not necessary.
For example : a = -2, b = 3
and (-2, 3) ∉ R₂ as |-2| ≤ 3
But (3, -2) ∉ R₂ because |3| ≤ -2
R₂ is not symmetric.
Transitivity : Let a, b, c ∈ R are such that
(a, b) ∈ R₂ and (b, c) ∈ R₂
(a, b) ∈ R₂ ⇒ |a| ≤ b …(1)
(b, c) ∈ R₂ ⇒ |b| ≤ c …(2)
From equation (1) and (2),
|a| ≤ b ≤ |b| ≤ c
⇒ |a| ≤ c
⇒ (a, c) ∈ R₂
So, (a, b) ∈ R₂, (b, c) ∈ R₂
⇒ (a, c) ∈ R₂ ∀ a, b, c ∈ R
R₂ is transitive.
Hence, from above it is clear that R₂ is not reflexive and symmetric relation.
It is only a transitive relation.

Question 25.
In a set of natural numbers, a relation R is defined as
aRb ⇔ a² – 4ab + 3b² = 0, (a, b ∈ N)
Prove that R is reflexive but not symmetric and transitive.
Solution:
Given set N = {1, 2, 3, 4,….}
A relation R in N is defined as
aRb ⇔ a² – 4ab + 3b² = 0, ∀ a, b ∈ N

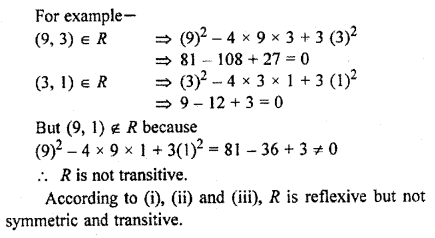
Question 26.
In the set of real numbers R, two relations R₁ and R₂ are defined as
(i) aR₁b ⇔ |a| = |b|
(ii) aR₂b ⇔ |a| ≤ |b|
Prove that R₁ is an equivalence relation but R₂ is not.
Solution:
(i) Given set R = set of real numbers.
A relation R₁ in R is defined as
aR₁b = |a| = |b| ∀ a, b ∈ R
For proving is equivalence relation we have to prove that R₁ is reflexive, symmetric and transitive relation.

Question 27.
A relation R in set A = {1, 2, 3} is defined as:
R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (1, 3), (3, 1), (2, 3), (3, 2)}
Test the reflexivity, symmetricity and transitivity of R.
Solution:
Given : Set A = {1, 2, 3}
Relation R in A is defined as
R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (1, 3), (3, 1) (2, 3), (3, 2)}
(i) Reflexivity : Here
(1, 1) ∈ R
(2, 2) ∈ R
(3, 3) ∈ R
So, ∀ a ∈ A ⇒ (a, a) ∈ R
R is not reflexive.

(ii) Symmetricity :
Here
(1, 2) ∈ R ⇔ (2, 1) ∈ R
(2, 3) ∈ R ⇔ (3, 2) ∈ R
(1, 3) ∈ R ⇔ (3, 1) ∈ R
So, (a, b) ∈ R ⇒ (b, a) ∈ R
R is symmetric relation.

(iii) Transitivity:
(1, 2) ∈ R, (2, 1) ∈ R ⇔ (1, 1) ∈ R etc.,
So, by definition of transitive relation.
R is transitive if
(a, b) ∈ R, (b, c) ∈ R
⇒ (a, c) ∈ R ∀ a, b, c ∈ A

Question 28.
Find the domain of function
\(\frac { 1 }{ \sqrt { \left( x+1 \right) \left( x+2 \right) } }\)
Solution:
Let f(x) = \(\frac { 1 }{ \sqrt { \left( x+1 \right) \left( x+2 \right) } }\)
Function f(x) is defiined if (x + 1) (x + 2) > 0
x > -1, x > -2
⇒ x ∈ (-∞, -2) ∪ (-1, ∞)
Hence, required domain (-∞, -2) ∪ (-1, ∞).

RBSE Solutions for Class 11 Maths