RBSE Solutions for Class 6 Maths Chapter 13 अनुपात व समानुपात Ex 13.1 is part of RBSE Solutions for Class 6 Maths. Here we have given Rajasthan Board RBSE Class 6 Maths Chapter 13 अनुपात व समानुपात Exercise 13.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 6 |
| Subject | Maths |
| Chapter | Chapter 13 |
| Chapter Name | अनुपात व समानुपात |
| Exercise | Ex 13.1 |
| Number of Questions | 12 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 6 Maths Chapter 13 अनुपात व समानुपात Ex 13.1
प्रश्न 1.
एक कस्बे में ग्रीष्मकालीन अवकाश में लगने वाले अभिरुचि शिविर में 25 लड़कियाँ और 15 लड़कों ने परिंडे बाँधे, अनुपात ज्ञात कीजिए।
(i) लड़कियों की संख्या(RBSESolutions.com)का लड़कों की संख्या से
(ii) लड़कियों की संख्या का कुल विद्यार्थियों की संख्या से।
हल :
लड़कियों की संख्या = 25
लड़कों की संख्या = 15
कुल संख्या = 25 + 15 = 40
(i) लड़कियों की संख्या को लड़कों की संख्या से,
अभीष्ट अनुपात = \(\frac { 25 }{ 15 } \) = \(\frac { 5 }{ 3 } \) = 5 : 3
(ii) अभीष्ट अनुपात = \(\frac { 25 }{ 40 } \) = \(\frac { 5 }{ 8 } \) = 5 : 8
![]()
प्रश्न 2.
वृक्षारोपण पखवाड़े में एक कक्षा के विद्यार्थियों ने 40 पौधे लगाए जिसमें 8 नीम के, 13 आम के, 19 करंजी के थे।
(i) नीम के पौधों व(RBSESolutions.com)आम के पौधों की संख्या में अनुपात।
(ii) कुल पौधों में से नीम के पौधों का अनुपात।
हल :
नीम के पेड़ = 8
आम के पौधे = 13
करंजी के पौधे = 19
कुल पौधे = 8 + 13 + 19 = 40
(i) अभीष्ट अनुपात = \(\frac { 8 }{ 13 } \) = 8 : 13
(ii) अभीष्ट अनुपात = \(\frac { 40 }{ 8 } \) = 5 : 1
![]()
प्रश्न 3.
आकृति को देखकर अनुपात बताइए।
(i) सभी त्रिभुजों की संख्या का वृत्तों की संख्या से।
(ii) सभी वर्गों की(RBSESolutions.com)संख्या का कुल आकृतियों से।
(iii) सभी त्रिभुजों की संख्या का कुल आकृतियों से।
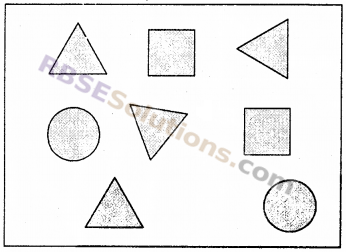
हल :
चित्र में,
त्रिभुज की संख्या = 4
वृत्तों की संख्या = 2
वत्तों की संख्या = 2
कुल आकृतियाँ = 4 + 2 + 2 = 8
(i) सभी त्रिभुजों की संख्या का वृत्तों की संख्या से
अभीष्ट अनुपात = \(\frac { 4 }{ 2 } \) = \(\frac { 2 }{ 1 } \) = 2 : 1
(ii) सभी वर्गों की संख्या का कुल आकृतियों से
अभीष्ट अनुपात = \(\frac { 2 }{ 8 } \) = \(\frac { 1 }{ 4 } \) = 1 : 4
(iii) सभी त्रिभुजों की संख्या का कुल आकृतियाँ से
अभीष्ट अनुपात = \(\frac { 4 }{ 8 } \) = \(\frac { 1 }{ 2 } \) = 1 : 2
![]()
प्रश्न 4.
रिक्त स्थानों को भरिए
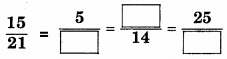
हल :
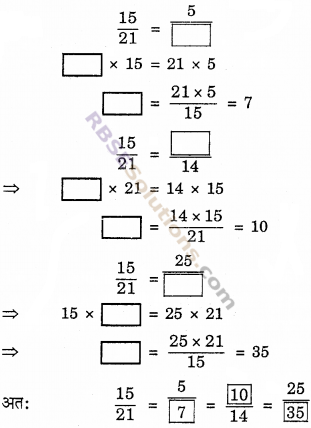
![]()
प्रश्न 5.
निम्न में से प्रत्येक का अनुपात ज्ञात कीजिए।
(i) 25 का 150 से
(ii) 72 का 36 से
(iii) 55 किमी. का 121 किमी. से
(iv) 35 मिनट का 55 मिनट से
हल :
(i) अभीष्ट अनुपात = \(\frac { 25 }{ 150 } \) = \(\frac { 1 }{ 6 } \) = 1 : 6
(ii) अभीष्ट अनुपात = \(\frac { 72 }{ 36 } \) = \(\frac { 2 }{ 1 } \) = 2 : 1
(iii) अभीष्ट(RBSESolutions.com)अनुपात = \(\frac { 55 }{ 121 } \) = \(\frac { 5 }{ 11 } \) = 5 : 11
(iv) अभीष्ट अनुपात = \(\frac { 35 }{ 55 } \) = \(\frac { 7 }{ 11 } \) = 7 : 11
![]()
प्रश्न 6.
निम्न में से प्रत्येक का अनुपात ज्ञात कीजिए।
(i) 60 पैसे तथा 3 रुपये
(ii) 800 ग्राम तथा 5 किग्रा.
(iii) 15 मिनट(RBSESolutions.com)तथा 1 घण्टा
(iv) 1 लीटर तथा 750 मिली.
हल :

![]()
प्रश्न 7.
एक गौशाला में वर्ष भर में 3,25,000 रुपये की राशि प्राप्त हुई और वर्ष भर गौ सेवा हेतु 3,00,000 रु. की राशि खर्च हुई। वर्ष भर की आय का वर्ष भर में खर्च की गई राशि से अनुपात ज्ञात कीजिए।
हल :
एक वर्ष की आय = 3,25,000 रु.
एक वर्ष का(RBSESolutions.com)खर्च = 3,00,000 रु.
\(\frac { 3,25,000 }{ 3,00,000 } \) = \(\frac { 325 }{ 300 } \)
⇒ \(\frac { 25\times 13 }{ 25\times 12 } \) = \(\frac { 13 }{ 12 } \) = 13 : 12
![]()
प्रश्न 8.
महेश प्रतिदिन 4 घण्टे स्वाध्याय करता है और लक्ष्मी प्रतिदिन 180 मिनट स्वाध्याय करती है। बताइए कि महेश और लक्ष्मी द्वारा किए गए स्वाध्याय में लगाए समय का अनुपात क्या होगा ? (1 घण्टा = 60 मिनट)
हल :
महेश प्रतिदिन स्वाध्याय करता है = 4 घण्टे
लक्ष्मी प्रतिदिन(RBSESolutions.com)स्वाध्याय करती है = 180 मिनट

![]()
प्रश्न 9.
एक विद्यालय में कुल 720 विद्यार्थी अध्ययन करते हैं जिसमें 360 विद्यार्थी छात्रावास में रहते हैं तो छात्रावास में रहने वाले विद्यार्थियों का कुल विद्यार्थियों के साथ अनुपात ज्ञात कीजिए।
हल :
कुल विद्यार्थी = 720
छात्रावास(RBSESolutions.com)में रहने वाले विद्यार्थी = 360
अभीष्ट अनुपात = \(\frac { 360 }{ 720 } \) = \(\frac { 1 }{ 2 } \) = 1 : 2
प्रश्न 10.
तलिस्मा व गुरुमित ने पापड़ उद्योग के लिए 2 : 5 में पूँजी लगाई। वर्ष के अन्त में 35,000 रुपये का मुनाफा हुआ तो प्रत्येक का हिस्सा ज्ञात कीजिए।
हल :
दिये गये अनुपातों का योग = 2 + 5 = 7
कुल मुनाफा = 35,000 रु.
तलिस्मा का हिस्सा = \(\frac { 2 }{ 7 } \) x 35,000 = 10,000 रु.
गुरुमित(RBSESolutions.com)का हिस्सा = \(\frac { 5 }{ 7 } \) x 35,000 = 25,000 रु.
![]()
प्रश्न 11.
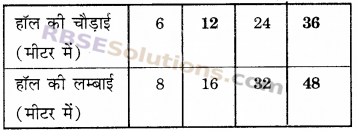
कथन को देखें-एक हॉल की चौड़ाई और लम्बाई का अनुपात 3 : 4 है। निम्न सारणी को पूरा कीजिए जो कि हॉल की कुछ सम्भव चौड़ाई और लम्बाई को दिखाती है।
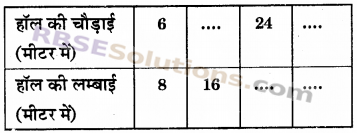
हल :

\(\frac { 25\times 13 }{ 25\times 12 } \) = \(\frac { 36 }{ 48 } \)
अत:
![]()
प्रश्न 12.
पिता की वर्तमान आयु 45 वर्ष और उसके पुत्र की 15 वर्ष है। अनुपात ज्ञात कीजिए
(i) पिता की वर्तमान आयु और पुत्र की वर्तमान आयु का।
(ii) पिता की आयु का पुत्र(RBSESolutions.com)की आयु से जब पुत्र 10 वर्ष का था।
(iii) 5 वर्ष बाद की पिता की आयु का 5 वर्ष बाद की पुत्र की आयु से।
(iv) पिता की आयु का पुत्र की आयु से जब पिता 60 वर्ष के होंगे।
हल :
पिता की वर्तमान आयु = 45 वर्ष
पुत्र की वर्तमान आयु = 15 वर्ष
(i) अभीष्ट अनुपात = \(\frac { 45 }{ 15 } \) = \(\frac { 3 }{ 1 } \) = 3 : 1
(ii) 5 वर्ष पहले (जब पुत्र 10 वर्ष का था) पिता की आयु = 45 – 5 = 40 वर्ष
तथा पुत्र की आयु = 15 – 5 = 10 वर्ष
अभीष्ट अनुपात = \(\frac { 40 }{ 10 } \) = \(\frac { 4 }{ 1 } \) = 4 : 1
(iii) 5 वर्ष बाद, पिता की आयु = 45 + 5 = 50 वर्ष
तथा पुत्र की(RBSESolutions.com)आयु = 15 + 5 = 20 वर्ष
अभीष्ट अनुपात = \(\frac { 50 }{ 20 } \) = \(\frac { 5 }{ 2 } \) = 5 : 2
(iv) जब पिता 60 वर्ष के होंगे (अर्थात् 15 वर्ष बाद) तो उस समय पुत्र की आयु = 15 + 15 = 30 वर्ष
अभीष्ठ अनुपात = \(\frac { 60 }{ 30 } \) = \(\frac { 2 }{ 1 } \) = 2 : 1
![]()
We hope the RBSE Solutions for Class 6 Maths Chapter 13 अनुपात व समानुपात Ex 13.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 6 Maths Chapter 13 अनुपात व समानुपात Exercise 13.1, drop a comment below and we will get back to you at the earliest.