RBSE Solutions for Class 6 Maths Chapter 5 Fractions In Text Exercise is part of RBSE Solutions for Class 6 Maths. Here we have given Rajasthan Board RBSE Class 6 Maths Chapter 5 Fractions In Text Exercise.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 6 |
| Subject | Maths |
| Chapter | Chapter 5 |
| Chapter Name | Fractions |
| Exercise | In Text Exercise |
| Number of Questions | 19 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 6 Maths Chapter 5 Fractions In Text Exercise
Page No. 56
Question 1.
Match the following (RBSESolutions.com) images (coloured parts) with fractions :
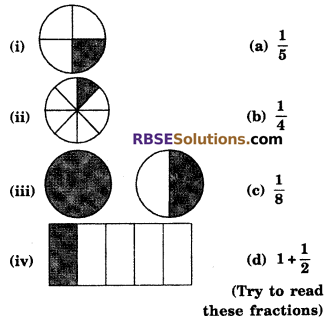
Solution.
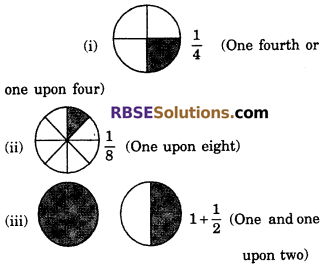

![]()
Page No. 58
Question 1.
Write the shaded part of the following (RBSESolutions.com) figures in the form of fractions.
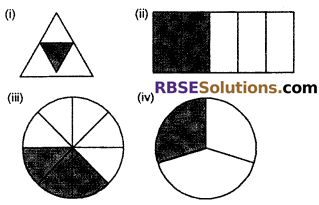
Solution.
Writing shaded part of the figures in the form of fraction –
(i) \(\frac { 1 }{ 4 } \)
(ii) \(\frac { 2 }{ 5 } \)
(iii) \(\frac { 3 }{ 8 } \)
(iv) \(\frac { 1 }{ 3 } \)
Page No. 59
Question 1.
Which of the following diagram is (RBSESolutions.com) right for \(\frac { 1 }{ 3 } \) and which is not ? State the reason as well.
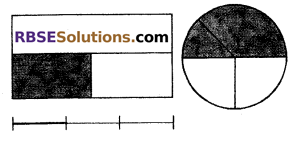
Solution.

This diagram is not right (RBSESolutions.com) for \(\frac { 1 }{ 3 } \), because in this diagram, all 3 parts are not, equal. This diagram makes 4 equal parts.

This diagram is not right for \(\frac { 1 }{ 3 } \), because in this diagram, all 3 parts are equal but shaded part is more than 1/3.
![]()
This diagram is right for \(\frac { 1 }{ 3 } \), because in this diagram, a line is divided into 3 equal parts and 1 part is shaded.
Question 2.
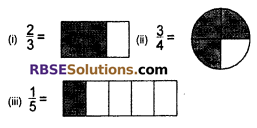
Show following fractions by (RBSESolutions.com) proper diagrams, (i) \(\frac { 2 }{ 3 } \) (ii) \(\frac { 3 }{ 4 } \) (iii) \(\frac { 1 }{ 5 } \)
Solution.
On showing given fractions by proper diagram –
Page No. 61
Question 1.
Express the following mixed (RBSESolutions.com) fractions into improper fractions.
(i) 3 \(\frac { 2 }{ 3 } \) (ii) 7 \(\frac { 1 }{ 9 } \)
Solution.
Improper fractions
![]()
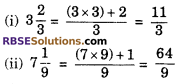
![]()
Page No. 64
Question 1.
Make three equivalent (RBSESolutions.com) fractions of the following.
(i) \(\frac { 3 }{ 4 } \)
(ii) \(\frac { 1 }{ 3 } \)
(iii) \(\frac { 2 }{ 7 } \)
Solution.
On making three equivalent fractions of given fractions –
(i) First equivalent fraction of \(\frac { 3 }{ 4 } \) = \(\frac { 3 }{ 4 } \) × \(\frac { 2 }{ 2 } \) = \(\frac { 6 }{ 8 } \)
Second equivalent fraction of \(\frac { 3 }{ 4 } \) = \(\frac { 3 }{ 4 } \) × \(\frac { 3 }{ 3 } \) = \(\frac { 9 }{ 12 } \)
Third equivalent fraction of \(\frac { 3 }{ 4 } \) = \(\frac { 3 }{ 4 } \) × \(\frac { 4 }{ 4 } \) = \(\frac { 12 }{ 16 } \)
Thus three equivalent fractions of \(\frac { 3 }{ 4 } \) are \(\frac { 6 }{ 8 } \),\(\frac { 9 }{ 12 } \) and \(\frac { 12 }{ 16 } \)
(ii) First equivalent (RBSESolutions.com) fraction of \(\frac { 1 }{ 3 } \) = \(\frac { 1 }{ 3 } \) × \(\frac { 2 }{ 2 } \) = \(\frac { 2 }{ 6 } \)
Second equivalent fraction of \(\frac { 1 }{ 3 } \) = \(\frac { 1 }{ 3 } \) × \(\frac { 3 }{ 3 } \) = \(\frac { 3 }{ 9 } \)
Third equivalent fraction of \(\frac { 1 }{ 3 } \) = \(\frac { 1 }{ 3 } \) × \(\frac { 4 }{ 4 } \) = \(\frac { 4 }{ 12 } \)
Thus, three equivalent fraction of \(\frac { 1 }{ 3 } \) are \(\frac { 2 }{ 6 } \), \(\frac { 3 }{ 9 } \) and \(\frac { 4 }{ 12 } \)
(iii) First equivalent fraction of \(\frac { 2 }{ 7 } \) = \(\frac { 2 }{ 7 } \) × \(\frac { 2 }{ 2 } \) = \(\frac { 4 }{ 14 } \)
Second equivalent fraction of \(\frac { 2 }{ 7 } \) = \(\frac { 2 }{ 7 } \) × \(\frac { 3 }{ 3 } \) = \(\frac { 6 }{ 21 } \)
Third equivalent fraction of \(\frac { 2 }{ 7 } \) = \(\frac { 2 }{ 7 } \) × \(\frac { 4 }{ 4 } \) = \(\frac { 8 }{ 28 } \)
Thus, three equivalent fractions of \(\frac { 2 }{ 7 } \) are \(\frac { 4 }{ 14 } \), \(\frac { 6 }{ 21 } \) and \(\frac { 8 }{ 28 } \)
Question 2.
Check which are the (RBSESolutions.com) equivalent fractions of the following?
(i) \(\frac { 5 }{ 10 } \) and \(\frac { 1 }{ 2 } \)
(ii) \(\frac { 3 }{ 7 } \) and \(\frac { 11 }{ 13 } \)
Solution.

Page No. 66
Question 1.
Dolly get a \(\frac { 1 }{ 5 } \) of the cake and Teenu gets \(\frac { 1 }{ 7 } \) of the cake. Then (RBSESolutions.com) who got the more cake?
Solution.
Dolly get part of cake = \(\frac { 1 }{ 5 } \)
Teenu get part of cake = \(\frac { 1 }{ 7 } \)
∵ Fractions \(\frac { 1 }{ 5 } \) and \(\frac { 1 }{ 7 } \) are unit fractions.
∴ Fractions with smaller denominator will be greater.
Thus, Dolly got more cake than Teenu, because fraction \(\frac { 1 }{ 5 } \) is greater than fraction \(\frac { 1 }{ 7 } \).
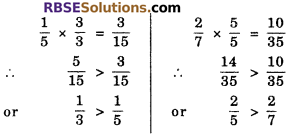
Question 2.
Which fraction (RBSESolutions.com) is greater?
(i) \(\frac { 1 }{ 3 } \) and \(\frac { 1 }{ 5 } \)
(ii) \(\frac { 2 }{ 5 } \) and \(\frac { 2 }{ 7 } \)
Solution.

![]()
Page No. 67
Question 1.
Write the following in (RBSESolutions.com) ascending and descending order.
(i) \(\frac { 3 }{ 7 } \) , \(\frac { 1 }{ 7 } \) , \(\frac { 4 }{ 7 } \) , \(\frac { 8 }{ 7 } \) , \(\frac { 6 }{ 7 } \)
(ii) \(\frac { 4 }{ 13 } \) , \(\frac { 12 }{ 13 } \) , \(\frac { 8 }{ 13 } \)
Solution.
(i) Since, denominators of all fractions are same, so fraction with greater numerator will be greater and fraction with smaller numerator will be smaller.

(ii) Since, denominators of all fractions are same. So (RBSESolutions.com) fraction with greater numerator will be greater and fraction with smaller numerator will be smaller.

Page No. 70
Question 1.
Solve the following
(i) \(\frac { 1 }{ 3 } \) + \(\frac { 2 }{ 3 } \)
(ii) \(\frac { 3 }{ 5 } \) + \(\frac { 2 }{ 7 } \)
(iii) \(\frac { 4 }{ 5 } \) + \(\frac { 7 }{ 15 } \)
Solution.

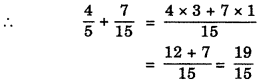
![]()
Page No. 60
Question 1.
Can you define (RBSESolutions.com) proper fraction?
Solution.
Yes, the fractions, where numerator is less than the denominator, are called proper fractions As : \(\frac { 4 }{ 9 } \) , \(\frac { 5 }{ 7 } \)
Question 2.
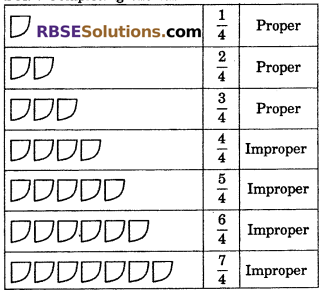
Rashmi has put some pieces of khakhre, O looking at these write them in the fractions and tell us which is proper and improper fraction.

Solution.
Completing (RBSESolutions.com) the table –
Page No. 63
Question 1.
Are all the coloured parts of unit (RBSESolutions.com) in following diagrams equal?
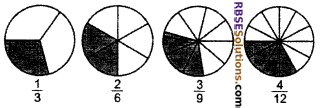
Solution.
Yes, all the coloured parts of unit of the given diagrams are equal, because fractions \(\frac { 2 }{ 6 } \),\(\frac { 3 }{ 9 } \) are equivalent fractions of \(\frac { 4 }{ 12 } \),\(\frac { 1 }{ 3 } \)
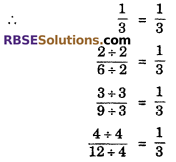
![]()
Page No. 65
Question 1.
Can you compare fractions like (RBSESolutions.com) numbers 18, 81, 28 ?
Solution.
Yes, we can compare fractions like number, if their denominators are same. But, if denominators are not same, then make them same and then compare.
Question 2.

Look at the above diagram and state (RBSESolutions.com) which fraction is smaller \(\frac { 1 }{ 3 } \) or \(\frac { 1 }{ 5 } \)
Solution.
It is shown from the diagram that fraction \(\frac { 1 }{ 5 } \) is smaller than fraction \(\frac { 1 }{ 3 } \), because \(\frac { 1 }{ 3 } \) is a part of 3 parts of a unit, and \(\frac { 1 }{ 5 } \) is a part of 5 parts of a unit.
Question 3.
Which is greater in unit fractions \(\frac { 1 }{ 4 } \) and \(\frac { 1 }{ 7 } \)
Solution.
Unit fraction \(\frac { 1 }{ 4 } \) is greater than fraction \(\frac { 1 }{ 7 } \), because \(\frac { 1 }{ 7 } \) is a part of 7 parts of a unit and \(\frac { 1 }{ 4 } \) is a part of 4 parts of a unit.
Page No. 66
Question 1.
Can you make rules for (RBSESolutions.com) comparisons of fractions?
Solution.
Yes, unit fraction always has 1 as numerator and denominator are different. Thus, the rule is that the fraction having smaller denominator will be greater fraction.
Activity
Page No. 62
Question 1.
Take a paper and colour it half. Fold it differently and (RBSESolutions.com) write the respective fraction. But be aware that all patts should be equal while folding.
Solution.

![]()
We hope the RBSE Solutions for Class 6 Maths Chapter 5 Fractions In Text Exercise will help you. If you have any query regarding Rajasthan Board RBSE Class 6 Maths Chapter 5 Fractions In Text Exercise, drop a comment below and we will get back to you at the earliest.