RBSE Solutions for Class 9 Maths Chapter 15 Statistics Ex 15.3 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 15 Statistics Exercise 15.3.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 15 |
| Chapter Name | Statistics |
| Exercise | Ex 15.3 |
| Number of Questions Solved | 12 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 15 Statistics Ex 15.3
Question 1.
A survey conducted by an organisation for the cause (RBSESolutions.com) of illness and death among the women between the ages 15 – 44 (in years) worldwide, found the following figures (in %)


(i) Represent the information given above graphically by a bar graph.
(ii) Which condition is the major cause (RBSESolutions.com) of women’s ill health and death worldwide?
Solution.
(i) We can represent the above data by a bar graph as shown below:
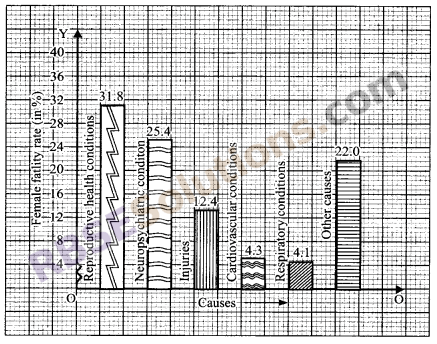
(ii) Reproductive health conditions is the major cause of women’s ill health and death worldwide.
![]()
Question 2.
The following data on the number (RBSESolutions.com) of girls (to the nearest ten) per thousand boys in different sections of Indian society is given below:
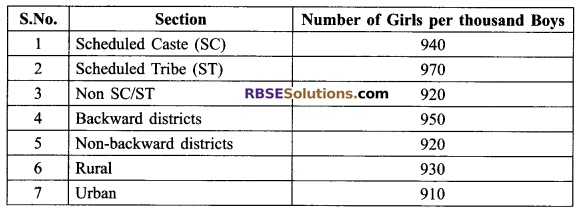
(i) Represent the information above by a bar graph.
(ii) In the class room, discuss what conclusions can be arrived from the graph.
Solution.
(i) Taking different sections of the society (RBSESolutions.com) on the x-axis and number of girls per thousand boys on the y-axis, we draw a bar graph to represent the above data.
We-take one unit of length along y-axis = 10 girls

(ii) (a) The number of girls per thousand boys under Non SC/ST and Non-backward districts are same as 920.
(b) Number of girls under section Scheduled Tribe (ST) per thousand boys is maximum i.e. 970 while minimum 910 in Urban section.
Question 3.
Given below are the seats won by different (RBSESolutions.com) political parties in the polling outcome of a state assembly elections.

(i) Draw a bar graph to represent the polling results.
(ii) Which political party won the maximum number of seats?
Solution.
(i) We draw the bar graph to represent the data, by taking political parties A, B, C, D, E, F along x-axis by taking suitable scale, say 10 small divisions = 10 seats.

(ii) Party A won maximum number of seats i.e., 75.
Question 4.
Construct histogram for the (RBSESolutions.com) following frequency table:

Solution.
We take OX and OY as x-axis and y-axis respectively on the graph paper and O as the origin. We represent class interval on the x-axis by choosing the scale as 1 cm = 5 units. We represent the frequency on y-axis by taking the scale as 1 cm = 4.
We now draw graph for the given frequency table, so rectangles A, B, C, D and E are constructed.
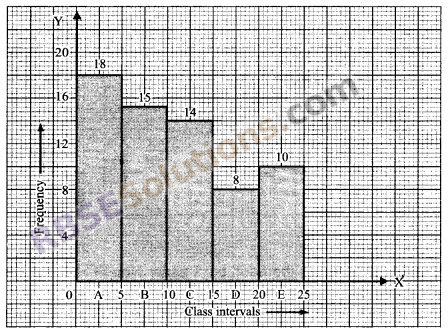
Question 5.
Construct histogram for the (RBSESolutions.com) following frequency table:

Solution.
Take OX and OY as x-axis and y-axis respectively on a graph paper and O as the origin. By taking suitable scale at x-axis (20 class interval = 1 cm) and y-axis (2 frequency = 1 cm), draw graph for the given frequency table.
So, rectangles A, B, C, D and E are constructed.
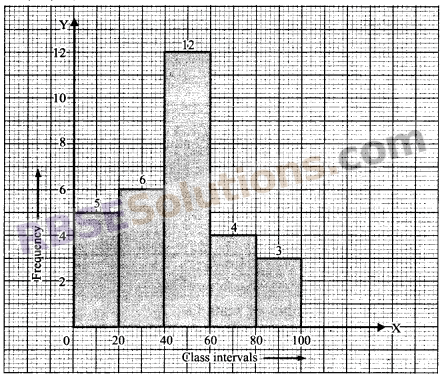
![]()
Question 6.
Construct histogram for the (RBSESolutions.com) following frequency table:

Solution.
Let us represent the class interval along x-axis and the frequency along y-axis. Since, the intervals are not of equal width, therefore we have to construct the rectangles with the classes as their bases and their corresponding heights will be as follows:
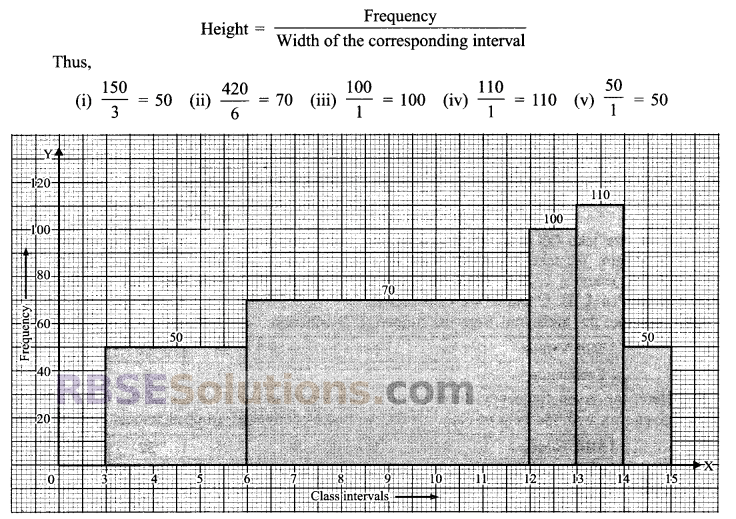
Question 7.
Construct histogram for the (RBSESolutions.com) following frequency distribution:

Solution.
The given frequency distribution is grouped but not continuous. So, first we will make them regular.
Lower limit of 2nd class interval =10;
Upper limit of 1 st class interval = 9
Difference (h) = 10 – 9 = 1
=>\(\frac { h }{ 2 }\) = \(\frac { 1 }{ 2 }\) = 0.5
We subtract 0.5 from lower limit and add 0.5 in upper limit to make class intervals regular.
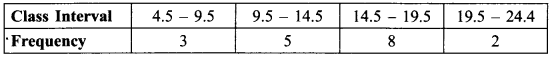
Now, this frequency distribution (RBSESolutions.com) table is grouped as well as continuous.
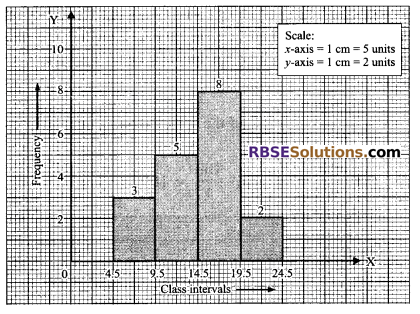
Here, we take OX and OY as x-axis and y-axis respectively on a graph paper with O as the origin. We take a suitable scale at x-axis (5 class intervals = 1 cm) and at the y-axis (2 frequency = 1 cm). Then we draw the graph for the given frequency distribution, so rectangles A, B, C and D are constructed.
Question 8.
Construct the histogram from (RBSESolutions.com) the following distribution.

Solution.
Here, the given frequency distribution is ungrouped and mid values of the distribution are given. So, with the help of class marks, we make continuous grouped frequency distribution.

We take OX and OY as x-axis and y-axis respectively on graph paper with O as the origin. We take suitable scale at x-axis (6 class intervals = 1 cm) and y-axis (5 frequency = 1 cm). Then we draw graph for the given frequency distribution, so rectangles A, B, C, D and E are constructed.

Question 9.
Construct a frequency polygon with the (RBSESolutions.com) help of histogram for the following frequency distribution.

Solution.
We take OX and OY as x-axis and y-axis respectively and O as the origin. By taking suitable scale at the x-axis as 1 cm = 5 units and y-axis as 1 cm = 1 unit, we draw graph of the given distribution and join the upper mid-point of the rectangles A, B, C, D, E and G. Hence, P’PQRSTUVV’ form the required frequency polygon.
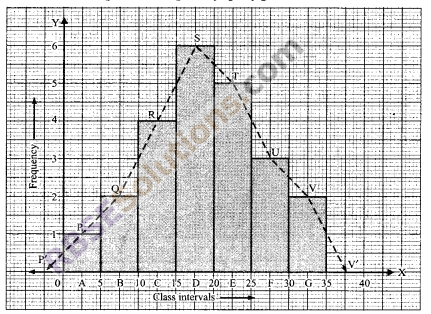
![]()
Question 10.
Construct a frequency polygon with the help (RBSESolutions.com) of histogram for the following frequency distribution. Maximum marks is 10.

Solution.
Here, we see that class interval 4 – 6 is repeated. So, we need to make certain modifications.

Now, we first draw a histogram for this data (RBSESolutions.com) and mark the mid-points of the tops of the rectangles obtained and join them. Then, ABCDEF is the required frequency polygon.
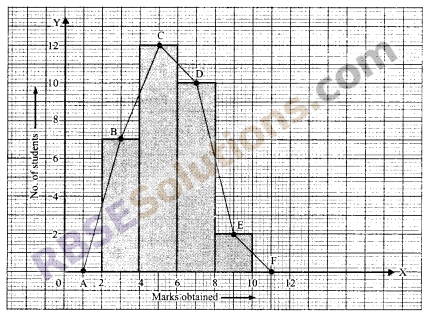
Question 11.
Construct a frequency polygon for the (RBSESolutions.com) following frequency distribution.
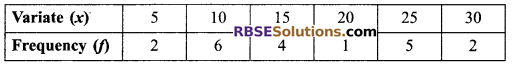
Solution.
The given distribution is ungrouped. So, by taking the scale 1 cm = 5 units along x-axis and 1 cm = 1 unit along y-axis respectively, we mark the variate and frequencies.
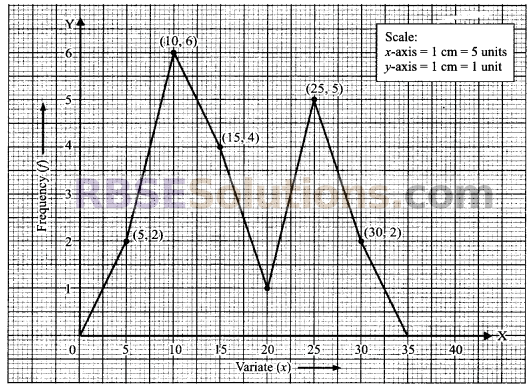
Now, the points (5, 2), (10, 6), (15, 4), (20, 1), (25, 5) and (30, 2) are plotted (RBSESolutions.com) and joined. Since, the value of the variate 0 comes before the first variate, so we join the first point (5, 2) to the origin (0, 0). Similarly, 35 comes ahead than the last variate, so we join the last point (30, 2) to the point (35, 0).
Thus, the required frequency polygon is obtained.
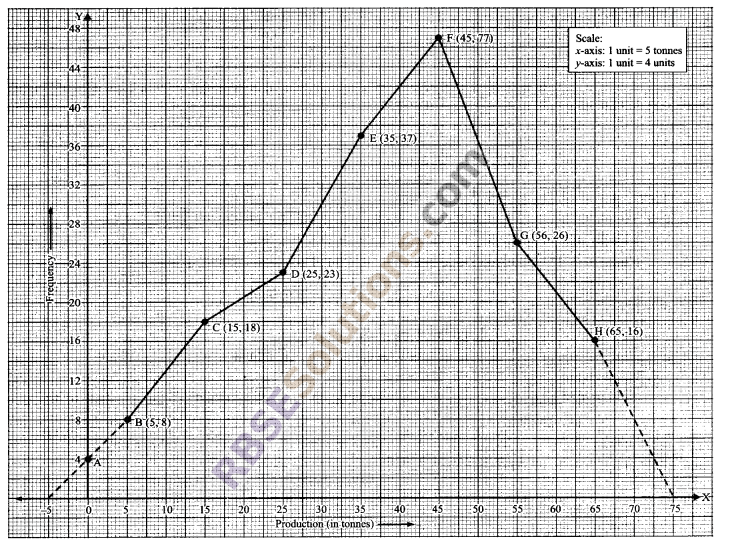
Question 12.
Construct a frequency polygon for the following frequency distribution.

Solution.
To draw a frequency polygon without a histogram, first we find the class-mark of the classes.
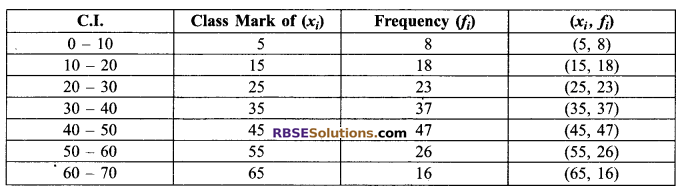
Now, we draw the frequency polygon by plotting the class (RBSESolutions.com) marks along the x-axis, the frequencies along the y-axis and then plotting and joining the points (xi, fi).
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 15 Statistics Ex 15.3 will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 15 Statistics Ex 15.3, drop a comment below and we will get back to you at the earliest.