RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions

RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions is part of RBSE Solutions for Class 9 Maths. Here we have given RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 2 Number System Additional Questions.

Board	RBSE
Class	Class 9
Subject	Maths
Chapter	Chapter 2
Chapter Name	Number System
Exercise	Additional Questions
Number of Questions Solved	40
Category	RBSE Solutions

RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions

Multiple Choice Questions

Question 1.
Which of the following (RBSESolutions.com) is irrational?
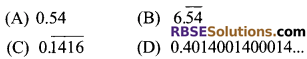
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 1
Solution
D

Question 2.
Between two rational (RBSESolutions.com) numbers, there is/ are:
(A) exactly one rational number
(B) no rational number
(C) infinitely many rational numbers
(D) only one rational number and no irrational number
Solution
C

Question 3.
\(0.34\overline { 67 } +0.13\overline { 33 } \) is equal to:
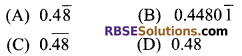
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 2
Solution
B

Question 4.
The rational number for the (RBSESolutions.com) recurring decimal 0.5353… is:
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 3
Solution
B

Question 5.
\(0.\overline { 36 } \) expressed in the (RBSESolutions.com) form \(\frac { p }{ q }\) equals to:
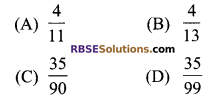
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 13
Solution
A

Question 6.
Decimal representation of an (RBSESolutions.com) irrational number is always:
(A) terminating repeating
(B) terminating
(C) non-terminating repeating
(D) non-terminating non-repeating
Solution
D

Question 7.
Every terminating decimal is:
(A) a natural number
(B) a rational number
(C) an integer
(D) a whole number
Solution
B

Question 8.
Which of the following (RBSESolutions.com) is different from others?
(A) √3
(B) √8
(C) √11
(D) √9
Solution
D

Question 9.
The value of \(0.\overline { 002 } \) in the form \(\frac { p }{ q }\), where p and q are (RBSESolutions.com) integers and q ≠ 0 is:
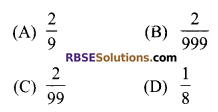
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 14
Solution
B

Question 10.
The value of √32÷√2 is equal to:
(A) √30
(B) 4
(C) \(\frac { 1 }{ 4 }\)
(D) 16
Solution
B

Very Short Answer Type Questions

Question 1.
Express the following in the form \(\frac { p }{ q }\), where p and q are (RBSESolutions.com) integers and q ≠ 0.
(i) \(0.\bar { 6 }\)
(ii) \(0.4\bar { 7 }\)
(iii) \(0.\bar { 001 }\)
Solution.
(i) \(0.\bar { 6 }\)
Let x = \(0.\bar { 6 }\) (Pure recurring decimal)
i.e. x = 0.6666 …(1)
Multiplying (1) by 10, because (RBSESolutions.com) ones digit i.e. 6 is repeating, we get
10x = 6.6666 …(2)
Subtracting (1) from (2), we get
10x – x = (6.6666…) – (0.6666…)
⇒ 9x = 6
⇒ x = \(\frac { 6 }{ 9 }\)
⇒ x = \(\frac { 2 }{ 3 }\)

(ii) Let x = \(0.4\bar { 7 }\) (Mixed recurring decimal)
i.e. x = 0.47777 …(1)
Multiplying (1) by 10, to make it (RBSESolutions.com) pure recurring decimal, we get
10x = 4.7777 …(2)
Further multiplying (2) by 10, we get
100x = 47.777 ….(3)
Subtracting (2) from (3), we get
100x – 10x = (47.777…) – (4.7777…)
⇒ 90x = 43
⇒ x = \(\frac { 43 }{ 90 }\)

(iii) Let x = \(0.\bar { 001 }\)
i.e. x = 0.001001001 …(1)
Multiplying (1) by 1000, we get
1000x = 1.001001 …(2)
Subtracting (1) from (2), we get
1000x – x = (1.001001…) – (0.001001…)
⇒ 999x = 1
⇒ x = \(\frac { 1 }{ 999 }\)

Question 2.
Express 3.2 in the form \(\frac { p }{ q }\), where p and q are (RBSESolutions.com) integers and q ≠ 0.
Solution.
Let x = \(3.\bar { 2 }\) (Pure recurring decimal)
i.e. x = 3.2222 ……(1)
Multiplying (1) by 10, we get
10x = 32.2222 ……(2)
Subtracting (1) from (2), we get
10x – x = (32.222…) – (3.222…)
⇒ 9x = 29
⇒ x = \(\frac { 29 }{ 9 }\)

Question 3.
Express \(15.\bar { 712 }\) as a fraction (RBSESolutions.com) in the simplest form.
Solution.
Let x = \(15.\bar { 712 }\)
i.e. x = 15.7121212 …(1)
Multiplying (1) by 10 and 100 successively, we get
10x = 157.121212 …(2)
and 1000x = 15712.1212 …(3)
Subtracting (2) from (3), we get
1000x – 10x = (15712.1212…) – (157.1212…)
⇒ 990x = 15555
⇒ x = \(\frac { 15555 }{ 990 }\)
⇒ x = \(\frac { 1037 }{ 66 }\)
Hence, \(15.\bar { 712 }\) = \(\frac { 1037 }{ 66 }\)

Question 4.
Is π is a rational (RBSESolutions.com) number?
Solution.
No, is an irrational number.
Reason: π is the ratio of the circumference of a circle to the length of its diameter. The value of π is approximately equal to \(\frac { 22 }{ 7 }\) but not exactly, i.e. π = 3.14159265…
Here in the value of π, no sign of recurrence of the digits was found.
Hence π is an irrational number.
But if we will take the value of π exactly equal to \(\frac { 22 }{ 7 }\) i.e. \(\frac { 22 }{ 7 }\) = \(3.\bar { 142857 }\) then it is said to be rational.

Question 5.
Express 0.00323232 … in the form \(\frac { p }{ q }\), where p and q are (RBSESolutions.com) integers and q ≠ 0.
Solution.
Let x = 0.00323232…
Then 100x = 0.323232 ……(1)
and 1000x = 32.323232 …(2)
Subtracting (1) from (2), we get
9900x = 32
⇒ x = \(\frac { 32 }{ 9900 }\)
⇒ x = \(\frac { 8 }{ 2475 }\)

Question 6.
Simplify each of the (RBSESolutions.com) following expressions:
(i) (3 + √3)(2 + √2)
(ii) (3 + √3)(3 – √2)
(iii) (√5 + √2)2
(iv) (√5 – √2)(√5 + √2)
Solution.
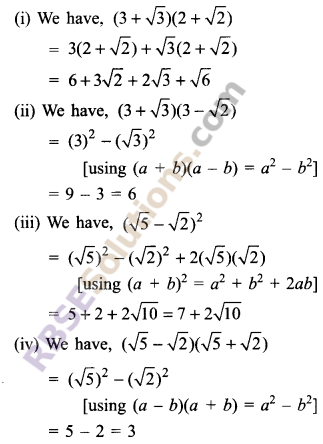
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 15

Question 7.
Simplify each of (RBSESolutions.com) the following:
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 16
Solution.

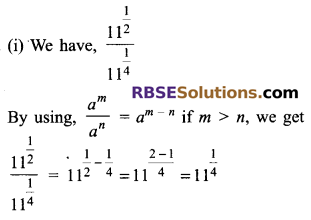
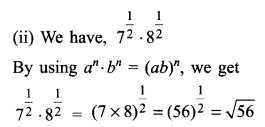
Question 8.
Simplify \(\left( \frac { 8 }{ 125 } \right) ^{ -\frac { 4 }{ 3 } }\)
Solution.
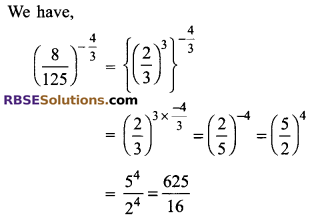
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 19

Question 9.
Solve for x: \(\left( \frac { 1 }{ 7 } \right) ^{ 4-2x }=\surd 7\)
Solution.
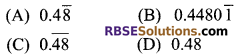
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 11

Question 10.
If \(\left( \frac { 1 }{ 5 } \right) ^{ 3y }\) = 0.008, then find (RBSESolutions.com) the value of (0.25)y
Solution.
We have, \(\left( \frac { 1 }{ 5 } \right) ^{ 3y }\) = 0.008
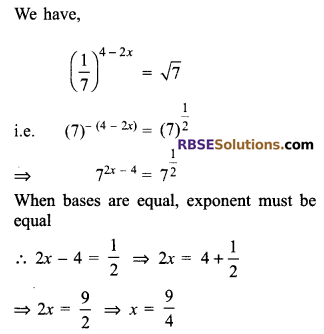
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 20

Short Answer Type Questions

Question 1.
Show how √5 can be represented (RBSESolutions.com) on the number line.
Solution.
On the number line, in the figure, we have marked two point O and P representing numbers 0 and 2 respectively.
We draw PQ = 1 unit ⊥r to the number line at P.
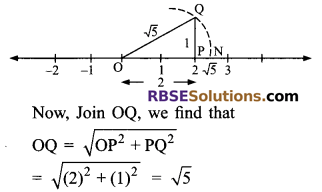
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 22
Now taking O as center and radius OQ = √5 we draw an arc which intersects the number line at the point N.
We observe that ON = √5 (radius)
Therefore, point N on the number line represents the irrational number √5

Question 2.
Locate √2 on the number line.
Solution.
On the number line, in the figure, we have (RBSESolutions.com) marked two points O and A representing numbers 0 and 1 respectively.
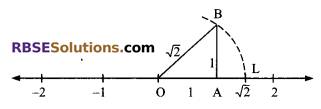
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 23
We draw AB = 1 unit ⊥r to the number line at A.
Now, join OB, we find that
OB = √(OA² + AB²) = √(1² + 1²) = √2
Now taking O as centre and radius OB = √2, we draw (RBSESolutions.com) an arc which intersect the number line at the point L.
We observe that OL = radius = √2.
Therefore, point L on the number line represents the irrational number √2.

Question 3.
Locate √11 on the number line.
Solution.
On the number line, point O represent 0 and (RBSESolutions.com) the point L represents 3.
Thus, we have OL = 3 units.
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 24
Now, with O as centre and radius ON = √11 we draw an arc which (RBSESolutions.com) intersect the number line at the point R.
We observe that OR = √11 (radius).
Therefore, the point R on the number line represents the irrational number √11.

Question 4.
Express \(2.4\bar { 178 }\) in the form \(\frac { p }{ q }\), where p and q are integers and q ≠ 0.
Solution.
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 25

Question 5.
Find two irrational (RBSESolutions.com) number between \(\frac { 1 }{ 7 }\) and \(\frac { 2 }{ 7 }\).
Solution.
On dividing 1 by 7, we get
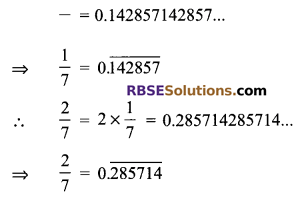
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 26
To find a irrational number between \(\frac { 1 }{ 7 }\) and \(\frac { 2 }{ 7 }\), we find numbers which are non- terminating and non-repeating. There are such infinite numbers.
Two of them may be (RBSESolutions.com) considered as 0.150150015000…, 0.220220022000…

Question 6.
Show that 0.142857142857… = \(\frac { 1 }{ 7 }\).
Solution.
Suppose x = 0.142857142857 …….. (i)
Multiplying (i) by 1000000, we get
1000000x = 142857.142857 …….. (ii)
Subtracting (i) from (ii), we get 999999x = 142857
999999x = 142857
x = \(\frac { 1 }{ 7 }\)
Hence, 0.142857142857… = \(\frac { 1 }{ 7 }\).

Question 7.
Rationalise the (RBSESolutions.com) denominator of \(\frac { 6 }{ \surd 12-\surd 3 }\)
Solution.
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 27

Question 8.
Find the value of x, if \(\sqrt [ 3 ]{ 3x-2 } =4\)
Solution.
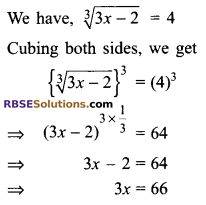
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 28
⇒ x = 22

Question 9.
Express the following irrational numbers/surds with (RBSESolutions.com) a rational denominator.
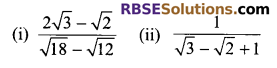
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 29
Solution.

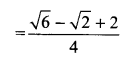
Question 10.
Rationalise the (RBSESolutions.com) denominator of \(\frac { { a }^{ 2 } }{ \sqrt { { a }^{ 2 }+{ b }^{ 2 } } +b }\)
Solution.
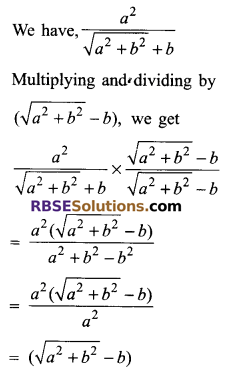
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 33

Long Answer Type Questions

Question 1.
Visualize 3.765 on the number line (RBSESolutions.com) using successive magnification.
Solution.
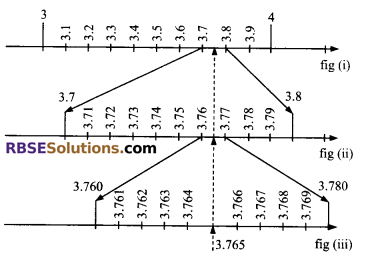
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 34
In figure (i) we observe the location of 3.765 between 3 and 4. Now, we magnify (RBSESolutions.com) the line segment between 3.7 and 3.8 and divide it into ten equal parts as shown in figure (ii). The location of the number 3.765 is in between 3.760 and 3.780. Again we magnify the line segment between 3.760 and 3.780 and divide further into ten equal parts. The position of the number 3.765 is clearly located at the number line as shown in figure (iii).

Question 2.
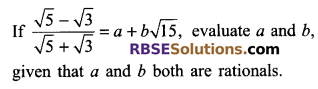
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 35
Solution.

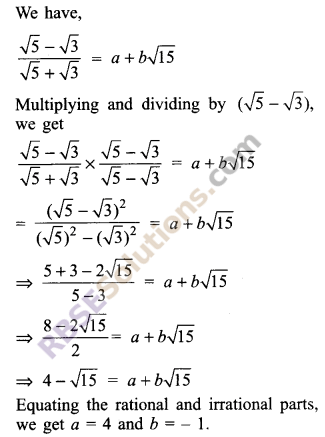
Question 3.
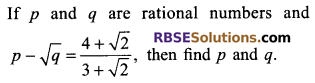
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 37
Solution.

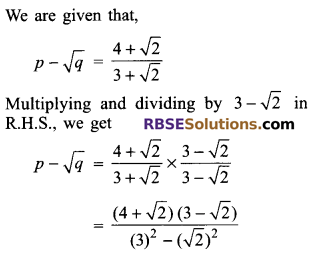
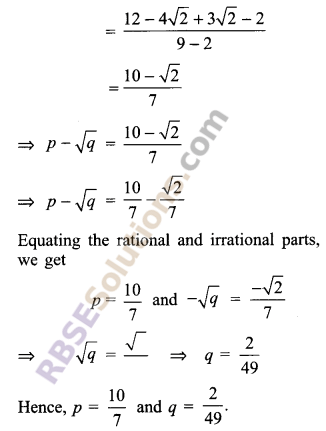
Question 4.
Rationalize the (RBSESolutions.com) denominator and simplify
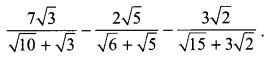
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 40
Solution.

Question 5.
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 43
Solution.

Question 6.
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 45
Solution.

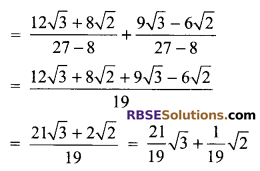
Question 7.
Simplify the (RBSESolutions.com) following:
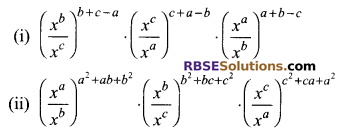
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 48
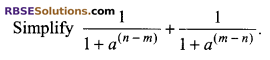
Solution.

Question 8.
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 50
Solution.

Question 9.
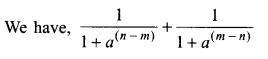
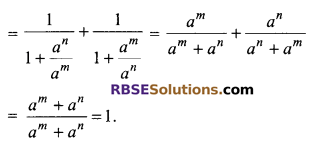
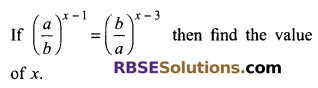
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 53
Solution.

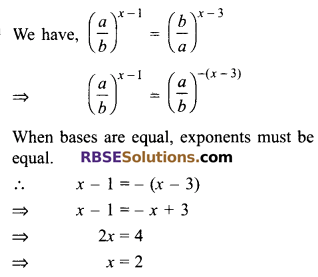
Question 10.
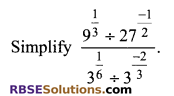
RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions 55
Solution.

We hope the given RBSE Solutions for Class 9 Maths Chapter 2 Number System Additional Questions will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 2 Number System Additional Questions, drop a comment below and we will get back to you at the earliest.