RBSE Solutions for Class 9 Maths Chapter 3 Polynomial Ex 3.4 is part of RBSE Solutions for Class 9 Maths. Here we have given RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 3 Polynomial Ex 3.4.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 3 |
| Chapter Name | Polynomial |
| Exercise | Ex 3.4 |
| Number of Questions Solved | 7 |
| Category | RBSE Solutions |
RBSE Solutions for Class 9 Maths Chapter 3 Polynomial Ex 3.4
Question 1.
Determine which of the following (RBSESolutions.com) polynomials has x – 1 factor.
(i) x4 – 2x3 – 3x2 + 2x + 2
(ii) x4 + x3 + x2 + x + 1
(iii) x4 + 3x3 – 3x2 + x – 2
(iv) x3 – x2 – (2 + √3)x + √3
Solution.
(i) Let p(x) = x4 – 2x3 – 3x2 + 2x + 2 and
g(x) = x – 1
If x – 1 i.e. g(x) be (RBSESolutions.com) a factor of p(x) then
P(1) = 0
Now p(1) = (1)4 – 2(1)3 – 3(1)2 + 2(1) + 2
= 1 – 2 – 3 + 2 + 2 = 0
∵ p(1) = 0
=> x – 1 is a factor of
p(x) = x4 – 2x3 – 3x2 + 2x + 2.
(ii) Let p(x) = x4 + x3 + x2 + x + 1
If x – 1 is a factor of p(x) then p(1) = 0
p(1) = (1)4 + (1)3 + (1)2 + (1) + 1
= 1 + 1 + 1 + 1 + 1 = 5
p(1) ≠ 0
∴ x – 1 is a factor of x4 + x3 + x2 + x + 1.
(iii) Let p(x) = x4 + 3x3 – 3x2 + x – 2
If x – 1 is (RBSESolutions.com) a factor of p(x) then p(1) = 0
∴ p(1) = (1)4 + 3(1)3 – 3(1)2 + (1) – 2
= 1 + 3 – 3 + 1 – 2 = 0
p(1) = 0
∴ x – 1 is a factor of x4 + 3x3 – 3x2 + x – 2.
(iv) Let p(x) = x3 – x2 – (2 + √3)x + √3
If x – 1 is a factor of p(x) then p(1) = 0
∴ p(1)= (1)3 – (1)2 – (2 + √3)(1) + √3
= 1 – 1 – 2 – √3 + √3 = -2
∴ p( 1) ≠ 0
Hence, x – 1 is not a factor of x3 – x2 – (2 + √3)x + √3
![]()
Question 2.
Use the factor theorem (RBSESolutions.com) to determine whether g(x) is a factor of p(x) in each of the following case.
(i) p(x) = 3x3 – x2 – 3x + 1; g(x) = x + 1
(ii) p(x) = 2x4 – 7x3 – 13x2 + 63x – 45; g(x) = x – 1
(iii) p(x) = 3x3 + 3x2 + 3x + 1; g(x) = x + 2
(iv) p(x) = 2x3 + x2 – 2x – 1; g(x) = 2x + 1
Solution.
(i) Here p(x) = 3x3 – x2 – 3x + 1 and g(x) = x + 1
Now we will try to find p(- 1). If p(- 1) = 0 then we say that g(x) is a factor of p(x) otherwise not.
Now p(- 1) = 3(- 1)3 – (- 1)2 – 3(- 1) + 1
= 3(- 1) – (1) + 3 + 1
= -3 – 1 + 3 + 1 = 0
p(1) = 0
∴ g(x) is a factor of p(x)
i.e. x + 1 is a factor of 3x3 – x2 – 3x + 1.
(ii) Here
p(x) = 2x4 – 7x3 – 13x2 + 63x – 45
and g(x) = x – 1
Now
p( 1) = 2(1)4 – 7(1)3 – 13(1)2 + 63(1) – 45
= 2 – 7 – 13 + 63 – 45
= – 65 + 65 = 0
p( 1) = 0
i.e. x – 1 is a factor of 2x4 – 7x3 – 13x2 + 63x – 45
(iii) Here p(x) = 3x3 + 3x2 + 3x + 1 and g(x) = x + 2
Now
p(- 2) = 3(- 2)3 + 3(- 2)2 + 3(- 2) + 1 = -24 + 12 – 6 + 1 = – 30 + 13 = -17
P(- 2) ≠ 0
i.e. x + 2 is not a factor of 3x3 + 3x2 + 3x + 1
(iv) Here p(x) = 2x3 + x2 – 2x – 1 and
g(x) = x + 1
Now
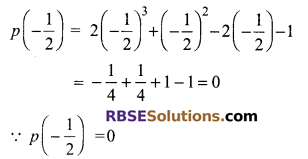
i.e. 2x + 1 is a factor of 2x3 + x2 – 2x – 1.
Question 3.
Find the (RBSESolutions.com) value of k, when x – 5 is a factor of x3 – 3x2 + kx – 10.
Solution.
Let p(x) = x3 – 3x2 + kx – 10
When x – 5 is a factor of p(x) then P( 5) = 0
⇒ (5)3 – 3(5)2 + k x 5 – 10 = 0
⇒ 125 – 75 + 5k – 10 = 0
⇒ 5k – 40 = 0
k = \(\frac { 40 }{ 5 }\) = 8
Hence, k = 8
Question 4.
Find the value of k, when x – 1 is a factor of 2x2 + kx + √2
Solution.
Let p(x) = 2x2 + kx + √2
When x – 1 is a factor of p(x) then p(1) = 0
⇒ 2(1)2 + k(1) + √2 = 0
⇒ 2 + k + √2 = 0
⇒ k = -(2 + √2)
![]()
Question 5.
If (x + 1) and (x – 1) are the (RBSESolutions.com) factors of x4 + ax3 – 3x2 + 2x + b then find the values of a and b.
Solution.
Let p(x) = x4 + ax3 – 3x2 + 2x + b
∵ (x + 1) is a factor of p(x)
∴ P(- 1) = 0
=> (-1)4 + a(-1)3 – 3(- 1)2 + 2(- 1) + b = 0
=> 1 – a – 3 – 2 + b = 0
=> – a + b = 4 ….(i)
Also (x – 1) is a factor of p(x)
∴ P( 1) = 0
=> (1)4 + a(1)3 – 3(1)2 + 2(1) + b = 0
=> 1 + a – 3 + 2 + 6 = 0
=> a + b = 0 …(ii)
Solving (i) and (ii), we get
2b – 4 => b = 2
Substituting b = 2 in (ii), we get
a + 2 = 0 => a = -2
Hence, a = – 2, b = 2
Question 6.
Factorise by splitting (RBSESolutions.com) middle term
(i) 3x2 + 7x + 2
(ii) 4x2 – x – 3
(iii)12x2 – 7x + 1
(iv) 6x2 + 5x – 6
Solution.
(i) Let p(x) = 3x2 + 7x + 2
Here we have to split middle term of p(x)
i.e. 7 into two parts such (RBSESolutions.com) that their sum is 7 and product is 2 x 3 = 6.
6 and 1 are such numbers whose sum is 7 and product is 6
∴ 3x2 + 7x + 2 = 3x2 + 6x + x + 2
= 3x(x + 2) + 1(x + 2)
= (x + 2)(3x + 1)
(ii) Let p(x) = 4x2 – x – 3
Here we have to split middle term – 1 into two parts such that their sum is – 1 product is 3 × – 4 = – 12
– 4 and 3 are such numbers whose sum is – 1 and product is – 12
4x2 – x – 3 = 4x2 – 4x + 3x – 3
= 4x(x – 1) + 3(x – 1)
= (x – 1 )(4x + 3)
(iii) Let p(x) = 12x2 – 7x + 1
Here we have to split middle term – 7 into (RBSESolutions.com) two parts such that their sum is – 7 and product is 12 × 1 = 12
– 4 and – 3 are such numbers whose sum is – 7 and product is 12
12x2 – 7x + 1 = 12x2 – 4x – 3x + 1
= 4x(3x – 1) – 1(3x – 1)
= (3x – 1)(4x – 1)
(iv) Let p(x) = 6x2 + 5x – 6
Here we have to split middle term 5 into two parts such that their sum is 5 and product is 6 × – 6 = – 36
9 and – 4 are such numbers whose sum is 5 and product is – 36. .
6x2 + 5x – 6 = 6x2 + 9x – 5x – 6
= 3x(2x + 3) – 2(2x + 3) = (2x + 3)(3x – 2)
![]()
Question 7.
Find the zeroes of (RBSESolutions.com) the polynomials:
(i) x3 + 6x2 + 11x + 6
(ii) x3 + 2x2 – x – 2
(iii) x4 – 2x3 – 7x2 + 8x + 12
(iv) x3 – 2x3 – x + 2
(v) x3 – 3x2 – 9x – 5
(vi) x3 – 23x2 + 142x – 120
Solution.
(i) Let the given (RBSESolutions.com) polynomial be
p(x) = x3 + 6x2 + 11x + 6
The coefficient of the leading term is 1
and the constant term is 6.






![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 3 Polynomial Ex 3.4 will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 3 Polynomial Ex 3.4, drop a comment below and we will get back to you at the earliest.