RBSE Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Miscellaneous Exercise is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Miscellaneous Exercise.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | दो चरों वाले रैखिक समीकरण |
| Exercise | Miscellaneous Exercise |
| Number of Questions Solved | 22 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Miscellaneous Exercise
विविध प्रश्नमाला
सही उत्तर को चुनिए : (प्रश्न 1 से 10 )
प्रश्न 1.
यदि y = 2x – 3 तथा y = 5 हो तो x का मान होगा
(A) 1
(B) 2
(C) 3
(D) 4
उत्तर
(D)
संकेत : y = 2x – 3
⇒ 2x = y + 3
⇒ x = \(\frac { y+3 }{ 2 }\) = \(\frac { 5+3 }{ 2 }\) = \(\frac { 8 }{ 2 }\) =4
प्रश्न 2.
यदि 2x + y = 6 हो तो इसको संतुष्ट करने वाला युग्म
(A) (1, 2)
(B) (2,1)
(C) (2, 2)
(D) (1, 1)
उत्तर : (C)
संकेत : 2x + y = 6 ⇒ y = 6 – 2x
x = 1 पर, y = 6 – 2(1) = 6 – 2 = 4
(x, y) = (1, 4)
x = 2 पर, y = 6 – 2 (2) = 6 – 4 = 2
(x, y) = (2, 2)
![]()
प्रश्न 3.

उत्तर
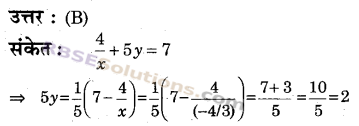
![]()
प्रश्न 4.
यदि \(\frac { 3 }{ x }\) + 4y = 5 तथा y = 1 हो, तो x का मान होगा:
(A) 3
(B) \(\frac { 1 }{ 3 }\)
(C) -3
(D) \(\frac { -1 }{ 3 }\)
उत्तर : (A)
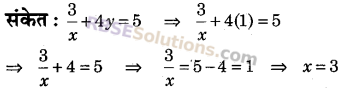
प्रश्न 5.
यदि x = 1 हो, तो समीकरण \(\frac { 4 }{ x }\) + \(\frac { 3 }{ y }\) = 5 में y का मान
(A) 1
(B) \(\frac { 1 }{ 3 }\)
(C) 3
(D) -3
उत्तर : (C)
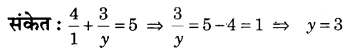
![]()
प्रश्न 6.
यदि किसी संख्या के इकाई तथा दहाई के स्थान पर अंक क्रमशः तथा x हों, तो संख्या होगी :
(A) 10x + y
(B) 10y + x
(C) x + y
(D) xy
उत्तर : (A)
संकेत : इकाई का अंक = y; दहाई का अंक = x
संख्या = 10x + y.
प्रश्न 7.
एक लड़के की आयु अपनी माता की आयु की एक तिहाई है। यदि माता की वर्तमान आयु x वर्ष है तो 12 वर्ष पश्चात् लड़के की आयु होगी :
(A) \(\frac { x }{ 2 }\) + 12
(B) \(\frac { x+12 }{ 3 }\)
(C) x + 4
(D) \(\frac { x }{ 3 }\) – 12
उत्तर : (A)
संकेत : माता की वर्तमान आयु x वर्ष है। लड़के की वर्तमान आयु माता की आयु की एक तिहाई है।
अत: लड़के की(RBSESolutions.com)वर्तमान आयु = \(\frac { x }{ 3 }\) वर्ष
अब लड़के की 12 वर्ष बाद आयु = \(\frac { x }{ 3 }\) + 12 वर्ष
![]()
प्रश्न 8.
x-अक्ष पर बिन्दु है-
(A) (2, 3)
(B) (2,0)
(C) (0, 2)
(D) (2, 2)
उत्तर : (B)
प्रश्न 9.
मूल बिन्दु के निर्देशांक हैं।
(A) (0, 0)
(B) (0, 1)
(C) (1, 0)
(D) (1, 1)
उत्तर : (A)
![]()
प्रश्न 10.
बिन्दु (3, -4) किस पाद में विद्यमान है?
(A) प्रथम
(B) द्वितीय
(C) तृतीय
(D) चतुर्थ
उत्तर : (D)
प्रश्न 11.
समीकरण 5y – 3x – 10 = 0 में 3 को x के रूप में व्यक्त कीजिए। वह बिन्दु ज्ञात कीजिए जहाँ समीकरण 5y – 3x – 10 = 0 द्वारा निरूपित रेखा y-अक्ष को काटती है।
हल

![]()
प्रश्न 12.
x के माने x = -2 से x = 2 तक एवं इनके मध्य लेते हुए समीकरण y = 2x + 1 के मानों से सारणी का निर्माण कीजिए तथा उक्त समीकरण का आलेख खीचिए।
हल
y = 2x + 1
x = -2 पर,
y = 2 (-2) + 1 = -4 + 1 = -3, बिन्दु (-2, -3)
x = -1 पर, y = 2(-1) + 1 = -2 + 1 = -1, बिन्दु (-1, -1)
x = 0 पर, y = 2 (0) + 1 = 0 + 1 = 1, बिन्दु (0, 1)
x = 1 पर, y = 2 (1) + 1 = 2 + 1 = 3, बिन्दु (1,3)
x = 2 पर, y = 2 (2) + 1 = 4 + 1 = 5, बिन्दु (2,5)
सारणी

आलेख
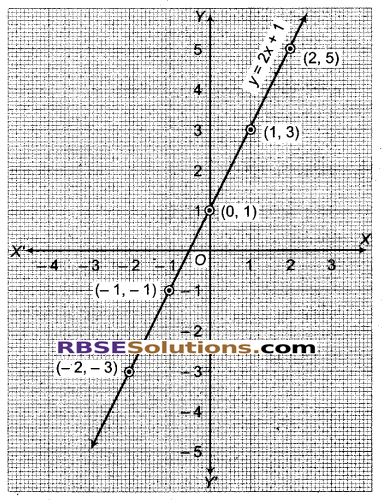
![]()
प्रश्न 13.
निम्न युगपत समीकरणों का हल ज्ञात कीजिए-
0.5x + 0.6y = 2.3; 0.2x + 0.7y = 23
हल
दिए गए समीकरण निकाय के दोनों पक्षों को 10 से गुणा करने पर
5x + 6y = 23 …(i)
2x + 7y = 23 …(ii)
समीकरण (i) में 2 से तथा (ii) में -5 से गुणा करके परस्पर जोड़ने पर
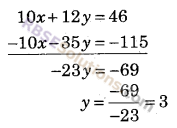
y का मान समीकरण (ii) में रखने पर
2x + 7 (3) = 23
⇒ 2x + 21 = 23
⇒ 2x = 23 – 21
⇒ x = 1
![]()
प्रश्न 14.
समीकरण निकाय 2x + 3y = 9; 3x + 4y = 5 का हल ज्ञात कीजिए।
हल
दिए गए समीकरण हैं :
2x + 3y = 9…(i)
तथा 3x + 4y = 5 …(i)
समीकरण (i) में 4 से तथा (ii) में -3 से गुणा करके परस्पर जोड़ने पर
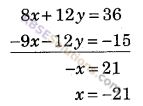
x का मान समीकरण (i) में रखने पर
2 (-21) +3 (y) = 9
⇒ -42 + 3y = 9
⇒ 3y = 9 + 42
⇒ y = 17
![]()
प्रश्न 15.
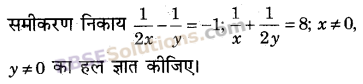
हल:


![]()
प्रश्न 16.
दो संख्याएँ इस प्रकार की हैं कि यदि छोटी संख्या में 7 जोड़ दिया जाय तो योग बड़ी संख्या से दुगुना हो जाता है तथा यदि बड़ी संख्या में 4 जोड़ दिया जाय तो योग छोटी संख्या से तिगुना हो(RBSESolutions.com)जाता है। दोनों संख्याओं को ज्ञात कीजिए।
हल:
माना छोटी संख्या x और बड़ी संख्या y है।
पहली शर्त के अनुसार,
x + 7 = 2
⇒ x – 2y = -7 …(i)
द्वितीय शर्त के अनुसार,
y + 4 = 3x
⇒ 3x – y = 4 …(ii)
⇒ y = 3x – 4
y का मान समीकरण (i) में रखने पर,
⇒ x – 2 (3x – 4) = -7
⇒ x – 6x + 8 = -7
⇒ -5x = -7 – 8
⇒ -5x = -15
⇒ x = 3
x = 3 समीकरण (ii) में रखने पर
3 × 3 – y = 4
⇒ y = 5
अतः छोटी संख्या x = 3 तथा बड़ी संख्या y = 5
![]()
प्रश्न 17.
किसी भिन्न का अंश, हर से 4 कम है। यदि अंश में से 2 घटा दिया जाए तथा हर में 1 जोड़ दिया जाए तो हर, अंश का 8 गुणा हो जाता है। भिन्न ज्ञात कीजिए।
हल:
माना भिन्न का अंश x तथा हर y है तो भिन्न = \(\frac { x }{ y }\)
प्रथम(RBSESolutions.com)शर्तानुसार, x = y – 4 ⇒ x – y = -4 …(i)
द्वितीय शर्तानुसार, 8 (x – 2) = y + 1
⇒ 8x – 16 = y + 1
⇒ 8x – y = 17 …(ii)
समीकरण (ii) में से (i) घटाने पर
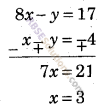
x का मान समीकरण (i) में रखने पर
3 – y = -4 ⇒ y = 3 + 4 = 7
![]()
प्रश्न 18.
5 पुस्तकों तथा 7 कलमों का कुल मूल्य 79 रु है। जबकि 7 पुस्तकों तथा 5 कलमों का कुल मूल्य 77 रु है। 1 पुस्तक तथा 2 कलमों का कुल मूल्य ज्ञात कीजिए।
हल:
माना एक पुस्तक का मूल्य x रुपये तथा एक कलम का मूल्य y रुपये है।
प्रथम(RBSESolutions.com)शर्तानुसार 5x + 7y = 79 ….(i)
द्वितीय शर्तानुसार 7x + 5y = 77 ….(ii)
समीकरण (i) में 5 से तथा (ii) में -7 से गुणा करके परस्पर जोड़ने पर,
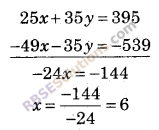
x का मान समीकरण (i) में रखने पर
5 × 6 + 7y = 79
⇒ 7y = 79 – 30 = 49
⇒ 7y = 49
⇒ y = 7
⇒ 2y = 14
अतः 1 पुस्तक का मूल्यं 6 रुपये तथा 2 कलमों का मूल्य 14 रुपयों तथा दोनों का कुल मूल्य (6 + 14) = 20 रुपये है।
![]()
प्रश्न 19.
दो अंकों की एक संख्या इस प्रकार की है कि जब इसे 9 से गुणा किया जाए तो वह उस संख्या की दुगुनी हो जाएगी जो मूल संख्या के अंकों के स्थान परस्पर बदलने से बनती है। यदि संख्या के दोनों अंकों का अंतर 7 हो, तो संख्या ज्ञात कीजिए।
हल:
माना एक संख्या का इकाई का अंक x तथा दहाई का अंक y है। दो अकों की संख्या = 10y + x
अंक परस्पर(RBSESolutions.com)बदलने से बनी संख्या = 10x + y
प्रश्न शर्तानुसार, (10y + x) × 9 = 2 (10x + y)
⇒ 90y + 9x = 20x + 2y
⇒ 20x – 9x – 90y + 2y = 0
⇒ 11x – 88y = 0
⇒ x – 8y = 0 …(i)
दूसरी शर्त के अनुसार, x – y = 7 …(ii)
समीकरण (ii) में से समीकरण (i) को घटाने पर,
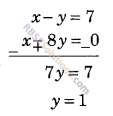
समीकरण (i) में y = 1 रखने पर
x – 8 × 1 = 0 ⇒ x – 8 = 0 ⇒ x = 8
मूल संख्या का इकाई का अंक = 8
और मूल(RBSESolutions.com)संख्या को दहाई का अंक = 1
मूल संख्या = 10y + x = 10 × 1 + 8 = 18
अतः मूल संख्या 18 होगी।
नोट- उपर्युक्त प्रश्न में अंकों का अन्तर y – x लेने पर x तथा y के मान ऋणात्मक रूप में प्राप्त होते हैं। जो कि गलत है।
![]()
प्रश्न 20.
एक त्रिभुज में ∠A = 3°, ∠B = 3° तथा ∠C = y° है। यदि 5x – 3y + 30 = 0 हो, तो सिद्ध कीजिए कि यह समकोण त्रिभुज है।
हल:
दिया है त्रिभुज ABC में,
∠A = x°, ∠B = 3x° तथा ∠C = y°
चूँकि, हम जानते हैं कि त्रिभुज के तीनों कोणों का योग 180° होता है।
x + 3x + y = 180
⇒ 4x + y = 180 ….(i)
दिया है, 5x – 3y + 30 = 0
⇒ 5x – 3y = -30 ……(ii)
समीकरण (i) में 3 से गुणा करके (ii) के साथ जोड़ने पर
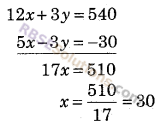
x का मान समीकरण (i) में रखने पर
4 x 30 + y = 180
⇒ y = 180 – 120 = 60
∠B = 3x = 3 × 30° = 90°
अतः त्रिभुज का कोण B = 90° है।
इससे स्पष्ट है कि त्रिभुज ABC एक समकोण त्रिभुज है।
![]()
प्रश्न 21.
निम्न युगपत समीकरणों का हल आलेख विधि से ज्ञात कीजिए।
(a) x + y = 4; x = y
(b) x + y = 3; 2x + 5y = 12
(c) 2x – 3y – 6 = 0; 2x + y + 10 = 0
(d) 2x + y – 3 = 0; 2x – 3y – 7 = 0
हल:
(a) दिया गया समीकरण निकाय है:
x + y = 4 …(i)
x = y …(ii)
चूंकि दोनों समीकरण x व y की प्रथम घात में हैं।
इनके आलेख(RBSESolutions.com)सरल रेखाएँ होंगी।
अब समीकरण x + y = 4 या y = 4 – x से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण x = y से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

अब बिन्दुओं (0, 4), (1, 3) तथा (3, 1) का आलेखन कर मिलाने से समीकरण x + y = 4 का आलेख तथा बिन्दुओं (1,1), (3, 3) तथा (5, 5) का आलेखन कर मिलाने से समीकरण x = y का आलेख प्राप्त होता है।
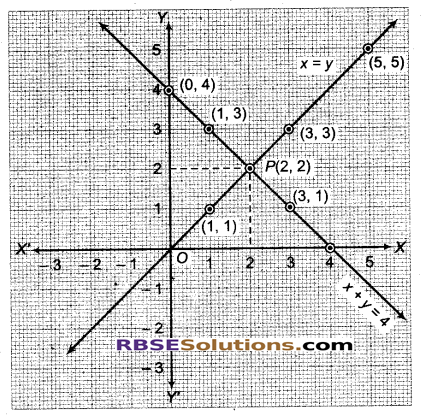
ये सरल रेखाएँ (आलेख) बिन्दु P पर प्रतिच्छेदित होती हैं, जिसके निर्देशांक (2, 2) हैं।
अत: x = 2, y = 2 दिए गए समीकरण(RBSESolutions.com)निकाय का अद्वितीय हल हैं।
(b) दिया गया समीकरण निकाय है-
x + y = 3 …(i)
2x + 5y = 12 …..(ii)
चूंकि, दोनों समीकरण x व y की प्रथम घात में हैं। इनके आलेख सरल रेखाएँ होंगी।
अब समीकरण x + y = 3 या y = 3 – x से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

अब बिन्दुओं (1, 2), (2,1) तथा (3,0) को आलेखन कर मिलाने से समीकरण x + y = 3 का आलेख तथा (1, 2), (-1.5, 3) तथा (3.5,1) का आलेखन कर मिलाने से समीकरण 2x + 5y = 12 का आलेख प्राप्त होता है।
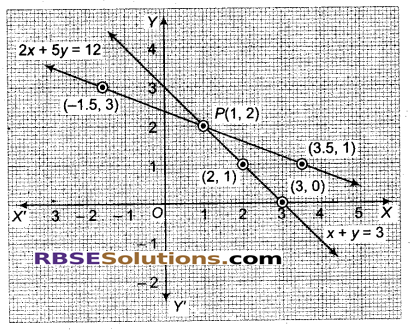
ये सरल रेखाएँ (आलेख) बिन्दु P पर प्रतिच्छेदित होती हैं, जिसके निर्देशांक (1, 2) हैं। अत: x = 1, y = 2 दिए गए निकाय के अद्वितीय हल हैं।
(c) दिया गया समीकरण निकाय है
2x – 3y – 6 = 0 …..(i)
2x + y + 10 = 0 …..(ii)
चूंकि दोनों समीकरण व y की प्रथम घात में हैं।
![]()
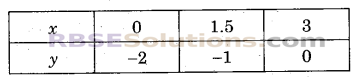
इनके आलेख सरल रेखाएँ होंगी। अब समीकरण 2x – 3y – 6 = 0 या y = \(\frac { 2x-6 }{ 3 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-
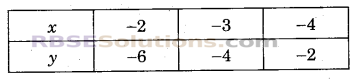
इसी प्रकार, समीकरण 2x + y + 10 = 0 या y = -2x – 10 से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-
अब बिन्दुओं (0, -2), (1.5, -1) तथा (3, 0) का आलेखन कर मिलाने से समीकरण 2x – 3y – 6 = 0 का आलेख तथा (-2, -6), (-3, -4) तथा (-4, -2) का आलेखन करे’ मिलाने से समीकरण 2x + y + 10 = 0 का आलेख प्राप्त होता है।
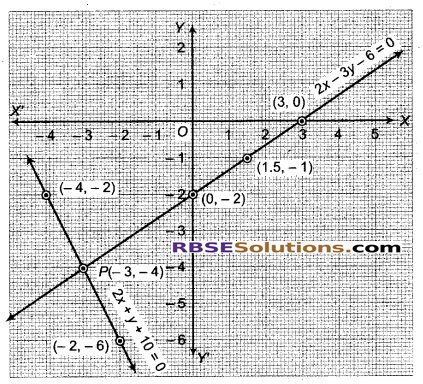
ये सरल रेखाएँ (आलेख) बिन्दु P पर प्रतिच्छेदित(RBSESolutions.com)होती हैं, जिसके निर्देशांक (-3, -4) हैं। अत: x = -3, y = -4 दिए गए निकाय के अद्वितीय हल हैं।
(d) दिया गया समीकरण निकाय है :
2x + y – 3 = 0 …..(i)
2x – 3y – 7 = 0 ……(ii)
चूँकि दोनों समीकरण x वे y की प्रथम घात में हैं।
![]()
इनके आलेख सरल रेखाएँ होंगी। अब समीकरण 2x + y – 3 = 0 या y = 3 – 2x से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण 2x – 3y – 7 = 0 या y = \(\frac { 2x-7 }{ 3 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-
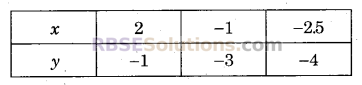
अब बिन्दुओं (0, 3), (1, 1) तथा (2, -1) का आलेखन कर मिलाने से समीकरण 2x + y – 3 = 0 का आलेख तथा (2, -1), (-1, -3) तथा (-2.5, -4) का आलेखन कर मिलाने से समीकरण 2x – 3y – 7 = 0 का आलेख प्राप्त होता है।
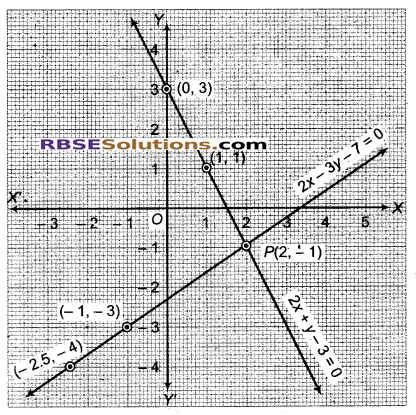
ये सरल रेखाएँ बिन्दु P पर प्रतिच्छेदित होती हैं, जिसके निर्देशांक (2, -1) हैं। अत: x = 2, y = -1 दिए गए समीकरण निकाय का अद्वितीय हल हैं।
![]()
प्रश्न 22.
समीकरण निकाय 2x – y = 1, x + 2y = 8 की आलेख विधि से हल ज्ञात कीजिए तथा(RBSESolutions.com)इनके संगत रेखाएँ y-अक्ष को जिन बिन्दुओं पर मिलती हैं उन बिन्दुओं के निर्देशांक ज्ञात कीजिए।
हल:
दिया गया समीकरण निकाय है-
2x – y = 1…(i)
तथा x + 2y = 8 …(ii)
चूंकि दोनों समीकरण x व y की प्रथम घात में हैं।
अत: इनके आलेख सरल रेखाएँ होंगी।
अब समीकरण 2x – y = 1 या y = 2x – 1 से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

इसी प्रकार, समीकरण x + 2y = 8 या y = \(\frac { 8-x }{ 2 }\) से (x, y) के विभिन्न मानों की निम्न सारणी प्राप्त होती है-

अब बिन्दुओं (0, -1), (2, 3) तथा (3, 5) का आलेखन कर मिलाने से समीकरण 2x – y = 1 का आलेख तथा (0, 4), (2, 3) तथा (4, 2) का आलेखन कर मिलाने से समीकरण x + 2y = 8 का आलेख प्राप्त होता है।
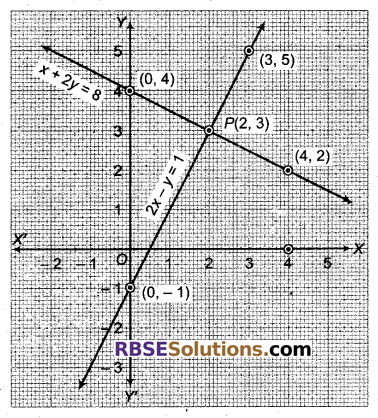
ये सरल रेखाएँ (आलेख) बिन्दु P पर प्रतिच्छेदित(RBSESolutions.com)होती हैं। जिसके निर्देशांक (2, 3) हैं। अत: x = 2, y = 3 दिए गए समीकरण निकाय का अद्वितीय हल हैं।
ग्राफ से स्पष्ट है कि ये रेखाएँ – अक्ष को जिन बिन्दुओं पर मिलती हैं, उनके निर्देशांक (0, -1) और (0, 4) है।
We hope the given RBSE Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Miscellaneous Exercise will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.