RBSE Solutions for Class 9 Maths Chapter 5 Plane Geometry and Line and Angle Miscellaneous Exercise is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 5 Plane Geometry and Line and Angle Miscellaneous Exercise.
| Board | RBSE |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 5 |
| Chapter Name | Plane Geometry and Line and Angle |
| Exercise | Miscellaneous Exercise |
| Number of Questions Solved | 16 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 5 Plane Geometry and Line and Angle Miscellaneous Exercise
Multiple Choice Questions (Q1 to Q7)
Question 1.
In the adjoining figure, if AB || CD || EF, PQ || RS, ∠RQD = 25° and ∠CQP = 60°, then (RBSESolutions.com) the value of ∠QRS.
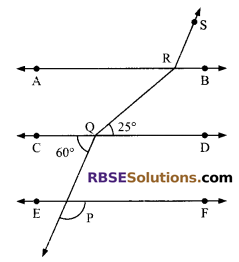
(A) 85°
(B) 135°
(C) 145°
(D) 110°
Question 2.
In figure, for what value of x, POQ is a line?
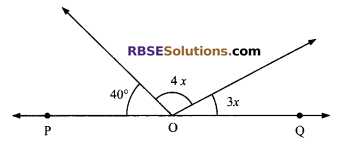
(A) 20°
(B) 25°
(C) 30°
(D) 35°
![]()
Question 3.
In figure, if OP || RS, ∠OPQ =110° and ∠QRS = 130° then ∠PQR is equal to
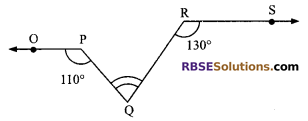
(A) 40°
(B) 50°
(C) 60°
(D) 70°
Question 4.
In figure, the (RBSESolutions.com) reflex ∠AOB is equal to:
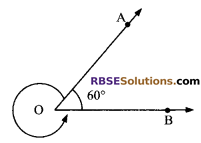
(A) 60°
(B) 120°
(C) 300°
(D) 360°
Question 5.
In figure, two lines AB and CD intersect at O. The angles at the (RBSESolutions.com) point O are marked in the figure. Then ∠x – ∠y is equal to:
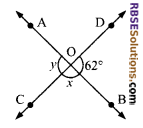
(A) 56°
(B) 118°
(C) 62°
(D) 180°
Question 6.
In figure, which of the following pairs of (RBSESolutions.com) angles are not corresponding angles:
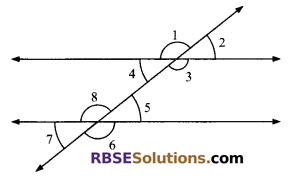
(A) ∠1, ∠5
(B) ∠2, ∠6
(C) ∠3, ∠7
(D) ∠3, ∠5
Question 7.
A transversal n intersects two parallel lines l and m at (RBSESolutions.com) points G and H respectively. The angles so formed have been marked in the figure, if ∠1 is an acute angle, which of the following statement is false:
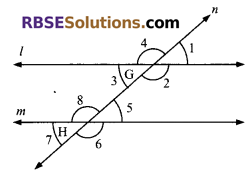
(A) ∠1 + ∠2 = 180°
(B) ∠2 + ∠5 = 180°
(C) ∠3 + ∠8 = 180°
(D) ∠2 + ∠6 = 180°
Question 8.
In figure, find the value of x.
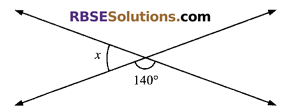
Solution.
∠x + 140° = 180° (linear pair)
⇒ x = 40°
Question 9.
In figure, AB || CD, find ∠x and ∠y from the (RBSESolutions.com) angles given in the figure.
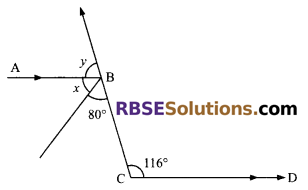
Solution.
Here it is given that AB || CD
∠x + 80° = ∠BCD (alt. angles)
⇒ ∠x + 80° = 116°
⇒ ∠x = 116° – 80°
⇒ ∠x = 36°
Now at point B
∠y + ∠x + 80° = 180° (straight angle)
⇒ ∠y = 180° – 116°
⇒ ∠y = 64°
Hence, ∠x = 36° and ∠y = 64°
![]()
Question 10.
In figure, lines l and m are parallel. Find ∠x and give (RBSESolutions.com) reasons for your answer.
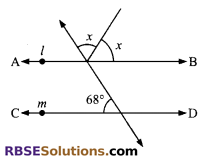
Solution.
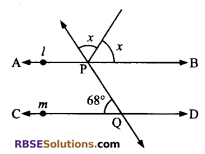
From figure, we (RBSESolutions.com) can write
x + x + ∠BPQ = 180° (straight angle)
⇒ 2x + ∠BPQ = 180°
∠BPQ = 180° – 2x …(i)
l || m
∠BPQ = 68° (alt. angle) …(ii)
From equations (i) and (ii), we have
68° = 180° – 2x
⇒ 2x = 180° – 68°
⇒ 2x = 112°
⇒ x = 56°
Question 11.
In figure, which of the lines are parallel to (RBSESolutions.com) each other and why? Give reasons?
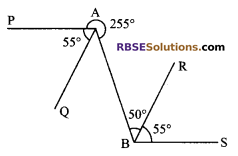
Solution.
As we know that if a number of lines meet at a point (RBSESolutions.com) then the sum of all the angles so formed = 360°
Here
∠PAQ + ∠QAB + reflex ∠PAB = 360°
⇒ 55° + ∠QAB + 255° = 360°
⇒ ∠QAB = 360° – 310°
⇒ ∠QAB = 50°
⇒ ∠QAB = ∠ABR = 50° (alt. angle)
QA || BR
Also ∠PAB = ∠ABS = 105° (alt. angles)
PA || BS
Hence QA || BR and PA || BS.
Question 12.
In the given figure, AC || PQ and AB || RS, then find ∠y. Also give (RBSESolutions.com) reasons in support of your answer.
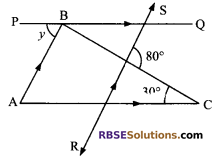
Solution.
PQ || AC ( given)
∠y = ∠BAC (alt. angles) …(i)
Again AB || RS (given)
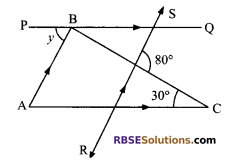
∠BAC = ∠LMC …(ii) (corresponding angles)
From (i) and (ii), we get
∠LMC = ∠y
In ΔLMC, exterior angle is equal to sum (RBSESolutions.com) of opposite interior angles
⇒ 80° = ∠y + 30°
⇒ ∠y = 80° – 30°
⇒ ∠y = 50°
Question 13.
In figure, AB || CD, PQ || EF, then find the value of x.
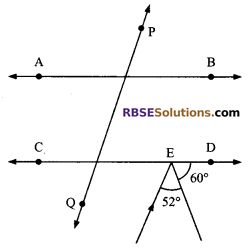
Solution.
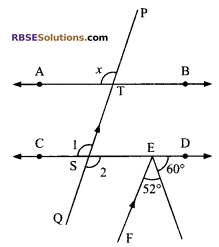
According to question
∠FEC + 52° + 60° = 180° (straight angle)
∠FEC = 180° – 112°
⇒ ∠FEC = 68°
Also AB || CD (given)
∠x = ∠CST (corresponding angles)
Also QP || EF (given)
∠QSE + ∠FES = 180° (The sum of the (RBSESolutions.com) interior angles on the same side of a transversal is 180°)
⇒ ∠QSE + 68° = 180°
⇒ ∠QSE = 180° – 68°
⇒ ∠QSE = 112° = ∠CST (vertically opposite angles)
x = ∠CST = 112° (corresponding angle).
![]()
Question 14.
In figure, find which of the lines l, m, n, p, q and r are parallel and why?
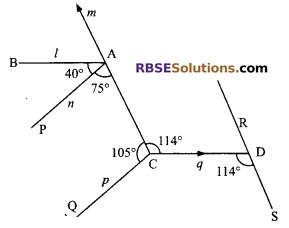
Solution.
∠PAC + ∠QCA = 75° + 105° = 180° (Sum of the interior angles)
n || p
Also ∠ACD = ∠CDS = 114° (alternate angles)
m || r
Hence n || p and m || r
Question 15.
In figure, the two lines intersect (RBSESolutions.com) each other. If ∠1 + ∠2 + ∠3 = 230°, then find the value of ∠1 and ∠4.
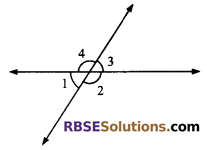
Solution.
According to question
∠1 + ∠2 + ∠3 + ∠4 = 360° (Angles formed at a point is 360°)
But ∠1 + ∠2 + ∠3 = 230° (given)
(∠1 + ∠2 + ∠3) + ∠4 = 360°
230° + ∠4 = 360°
∠4 = 360° – 230°
∠4 = 130°
But ∠1 + ∠4 = 180° (linear pair axiom)
∠1 + 130°= 180°
∠1 = 180°- 130° = 50°
Question 16.
Two plane mirrors PQ and QR are joint (RBSESolutions.com) together at Q with an angle of 30°. The incident ray AB parallel to the mirror RQ, then find the value of ∠BCQ, ∠CBQ and ∠BDC.
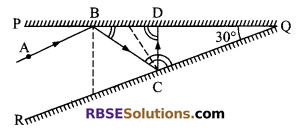
Solution.
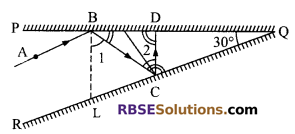
BL || CD
∠1 = ∠2 i.e. ∠LBC = ∠BCD
Also CD ⊥ PQ
⇒ ∠CDB = ∠CDQ = 90°
⇒ ∠DCQ = 180° – 120° = 60° = ∠DCB
as CD is bisector ∠BCQ
⇒ ∠BCQ = ∠BCD + ∠DCQ = 60° + 60° = 120°
In ∆CBD,
∠CBD + 90° + 60° = 180°
⇒ ∠CBD or ∠CBQ = 180° – 150° = 30°
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 5 Plane Geometry and Line and Angle Miscellaneous Exercise will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 5 Plane Geometry and Line and Angle Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.