RBSE Solutions for Class 9 Maths Chapter 5 Plane Geometry and Line and Angle Ex 5.1 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 5 Plane Geometry and Line and Angle Exercise 5.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 5 |
| Chapter Name | Plane Geometry and Line and Angle |
| Exercise | Ex 5.1 |
| Number of Questions Solved | 5 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Solutions Chapter 5 Plane Geometry and Line and Angle Ex 5.1
Question 1.
If angles of magnitude (2x + 4) and (x – 1) form (RBSESolutions.com) a linear pair. Find these angles.
Solution.
According to question
(2x + 4)° + (x – 1)° = 180°
(Linear pair axiom)
⇒ 3x + 3 = 180
⇒ 3x = 177
\(x=\frac { 177 }{ 2 }=59\)
∴Angles are (2 x 59 + 4)° = 122° and (59 – 1)° = 58
![]()
Question 2.
From the given figure
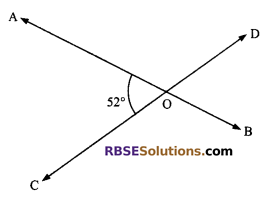
(i) Find the magnitude of ∠BOD
(ii) Find the magnitude of ∠AOD
(iii) Write the pair (RBSESolutions.com) of vertically opposite angles.
(iv) Name the adjacent supplementary angles of ∠AOC
Solution.
(i) ∠AOC = 52° (given)
⇒ ∠BOD = 52°
(Vertically opposite angles)
(ii) ∠AOC + ∠AOD = 180°
(Linear pair axiom)
⇒ 52° + ∠AOD = 180°
⇒ ∠AOD = 180° – 52°
⇒ ∠AOD = 128°
(iii) (∠AOC, ∠BOD) and (∠AOD, ∠BOC) are vertically opposite pairs of angles.
(iv) The adjacent supplementary angles of ∠AOC are ∠AOD and ∠BOC.
Question 3.
In the given figure, ∠PQR = ∠PRQ then (RBSESolutions.com) prove that ∠PQS = ∠PRT.
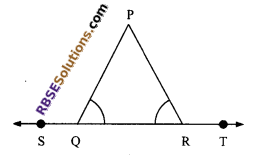
Solution.
We are given that ∠PQR = ∠PRQ ,..(i)
From figure,
∠PQS + ∠PQR = 180°
(linear pair axiom) …(ii)
and ∠PRT + ∠PRQ = 180°
(linear pair axiom) …(iii)
Using (ii) and (iii)
∠PQS + ∠PQR = ∠PRT + ∠PRQ
Again using (i) i.e. ∠PQR = ∠PRQ, we get
⇒ ∠PQS = ∠PRT
Hence proved
Question 4.
In figure OP, OQ, OR and OS are (RBSESolutions.com) four rays. Prove that
∠PPQ + ∠QOR + ∠SOR + ∠POS = 360°.
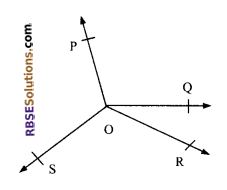
Solution.
In figure, we need to produce (RBSESolutions.com) any of the rays OP, OQ, OR or OS backwards to a point.
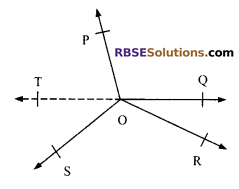
Let us produce ray OQ backwards to a point T so that TOQ is a line see figure.
Now, ray OP stands on line TOQ
Therefore, ∠TOP + ∠POQ = 180° …(i)
(Linear pair axiom)
Similarly, ray OS stands (RBSESolutions.com) on line TOQ.
Therefore, ∠TOS + ∠SOQ = 180° …(ii)
But ∠SOQ = ∠SOR + ∠QOR
So, (ii) becomes
∠TOS + ∠SOR + ∠QOR = 180° …(iii)
Now adding (i) and (iii), we get
∠TOP + ∠POQ + ∠SOR + ∠QOR = 360° …(iv)
But ∠TOP + ∠TOS = ∠POS
Therefore (iv) becomes
∠POQ + ∠QOR + ∠SOR + ∠POS = 360°
![]()
Question 5.
In the given figure, if
∠x + ∠y = ∠p + ∠q, then (RBSESolutions.com) prove that AOB is a line.
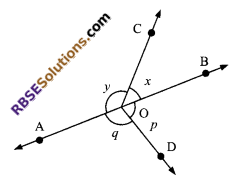
Solution.
Method I: In the given figure, let us (RBSESolutions.com) assume that AOB is a straight line
∴ ∠x + ∠y = 180°
(linear pair of angles) …(i)
and ∠p + ∠q = 180°
(linear pair of angles) …(ii)
From (i) and (ii), we get
∠x + ∠y = ∠p + ∠q
Hence proved
Method II: As we know that sum of the (RBSESolutions.com) angles around a point is 360°.
∴ ∠x + ∠y + ∠p + ∠q = 360°
or ∠x + ∠y + ∠x + ∠y = 360°
(∵ ∠x + ∠y = ∠p + ∠q)
2 (∠x + ∠y) = 360°
⇒ ∠x + ∠y = 180°
⇒ AOB is a straight line.
We hope the given RBSE Solutions for Class 9 Maths Chapter 5 Plane Geometry and Line and Angle Ex 5.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Solutions Chapter 5 Plane Geometry and Line and Angle Exercise 5.1, drop a comment below and we will get back to you at the earliest.