RBSE Solutions for Class 9 Maths Chapter 9 Quadrilaterals Miscellaneous Exercise

RBSE Solutions for Class 9 Maths Chapter 9 Quadrilaterals Miscellaneous Exercise is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 9 Quadrilaterals Miscellaneous Exercise.

Board	RBSE
Class	Class 9
Subject	Maths
Chapter	Chapter 9
Chapter Name	Quadrilaterals
Exercise	Miscellaneous Exercise
Number of Questions Solved	44
Category	RBSE Solutions

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 9 Quadrilaterals Miscellaneous Exercise

Multiple Choice Questions (Q1 to Q15)

Question 1.
Three angles of a quadrilateral are 75°, 90° and 75°. The (RBSESolutions.com) fourth angle is:
(A) 90°
(B) 95°
(C) 105°
(D) 120°
Answer.
(D) 120°

Question 2.
A diagonal of a rectangle is inclined to one side of the rectangle at 25°. The acute angle between the diagonals is:
(A) 55°
(B) 50°
(C) 40°
(D) 25°
Answer.
(B) 50°

Question 3.
ABCD is a rhombus (RBSESolutions.com) such that ∠ACB = 40°. Then ∠ADB is:
(A) 40°
(B) 45°
(C) 50°
(D) 60°
Answer.
(C) 50°

Question 4.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if:
(A) PQRS is a rectangle
(B) PQRS is a parallelogram
(C) diagonals of PQRS are perpendicular
(D) diagonals of PQRS are equal
Answer.
(C) diagonals of PQRS are perpendicular

Question 5.
The quadrilateral formed by joining the mid-points of the sides (RBSESolutions.com) of a quadrilateral PQRS, taken in order, is a rhombus, if:
(A) PQRS is a rhombus
(B) PQRS is a parallelogram.
(C) diagonals of PQRS are perpendicular
(D) diagonals of PQRS are equal
Answer.
(D) diagonals of PQRS are equal

Question 6.
If angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio 3 : 7 : 6 : 4, then ABCD is a:
(A) rhombus
(B) parallelogram
(C) trapezium
(D) kite
Answer.
(C) trapezium

Question 7.
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each (RBSESolutions.com) other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a:
(A) rectangle
(B) rhombus
(C) parallelogram
(D) a quadrilateral whose opposite angles are supplementary
Answer.
(D) a quadrilateral whose opposite angles are supplementary

Question 8.
If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, COQ and PQD form:
(A) a square
(B) a rhombus
(C) a rectangle
(D) any other parallelogram
Answer.
(C) a rectangle

Question 9.
The figure obtained by joining the midpoints (RBSESolutions.com) of the sides of a rhombus, taken in order is
(A) a rhombus
(B) a rectangle
(C) a square
(D) any parallelogram
Answer.
(B) a rectangle

Question 10.
D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively the DEQP is
(A) a square
(B) a rectangle
(C) a rhombus
(D) a parallelogram
Answer.
(D) a parallelogram

Question 11.
The figure formed by joining the mid¬points of the sides (RBSESolutions.com) of a quadrilateral ABCD, taken in order, is a square only if:
(A) ABCD is a rhombus
(B) diagonals of ABCD are equal
(C) diagonals of ABCD are equal and perpendicular
(D) diagonals of ABCD are perpendicular
Answer.
(C) diagonals of ABCD are equal and perpendicular

Question 12.
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32° and ∠AOB = 70°, then ∠DBC is equal to:
(A) 24°
(B) 86°
(C) 38°
(D) 32°
Answer.
(C) 38°

Question 13.
Which of the following is not true for a parallelogram?
(A) opposite sides are equal
(B) opposite angles are equal
(C) opposite angles are bisected by the diagonals
(D) diagonals bisect each other
Answer.
(C) opposite angles are bisected by the diagonals

Question 14.
D and E are the mid-points of the sides AB and AC respectively of ΔABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need (RBSESolutions.com) additional information which is:
(A) ∠DAE = ∠EFC
(B) AE = EF
(C) DE = EF
(D) ∠ADE = ∠ECF
Answer.
(C) DE = EF

Question 15.
Diagonals of a parallelogram ABCD intersect at O. If ∠BOC = 90° and ∠BDC = 50°, then ∠OAB is:
(A) 90°
(B) 50°
(C) 40°
(D) 10°
Answer.
(C) 40°

Question 16.
ABCD is a parallelogram. If its diagonals (RBSESolutions.com) equal, then find the value of ∠ABC.
Solution.
As diagonals of the parallelogram ABCD are equal, it is a rectangle.
Therefore, ∠ABC = 90°.

Question 17.
Diagonals of a rhombus are equal and perpendicular to each other. Is this statement true? Give reason for your answer.
Solution.
This statement is false because diagonals of a rhombus are perpendicular but not equal to each other.

Question 18.
Three angles of a quadrilateral ABCD are equal. Is it a parallelogram? Why or why not?
Solution.
It is not be a parallelogram, because we may have ∠A = ∠B = ∠C = 80° and D = 120°. Here, ∠B ≠ ∠D.

Question 19.
In quadrilateral ABCD, ∠A + ∠D = 180°. What special name can (RBSESolutions.com) be given to the quadrilateral?
Solution.
In quadrilateral ABCD,
∠A + ∠D = 180° (∵ AB || CD)
i.e. (sum of co-interior angles on the same side of traversal is 180°).
ABCD is a parallelogram.

Question 20.
All the angles of a quadrilateral are equal. What special name is given to the quadrilateral?
Solution.
If all the angles of a quadrilateral are equal then quadrilateral may be square or a rectangle.

Question 21.
Diagonals of a rectangle are equal and perpendicular. Is this (RBSESolutions.com) statement true? Give reason for your answer.
Solution.
This statement is not true as diagonal of a rectangle are equal but not perpendicular.

Question 22.
A square is inscribed in an isosceles right triangle so that the square and the triangle have one angle common. Show that the vertex of the square opposite to the vertex of the common angle bisects the hypotenuse.
Solution.

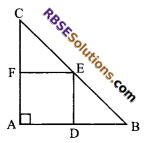
Given: ∆ABC in which ∠A = 90° and AB = AC
Let ADEF be a square
⇒ AD = AF …(i)
and AB = AC …(ii)
Subtracting equation (i) from (ii), we get
AB – AD = AC – AF
⇒ BD = CF …(iii)
Now in ∆CFE and ∆EDB
∠CFE = ∠EDB = 90°
BD = CF (proved earlier)
DE = EF (sides of a square)
∆CFE = ∆EDB (by SAS congruency rule)
⇒ CE = BE (by c.p.c.t)
Hence, vertex E of the square (RBSESolutions.com) bisects the hypotenuse BC.

Question 23.
In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC are produced to meet at F. Find the length of CF.
Solution.
In ∆ADE and ∆CEF
∠1 = ∠3 …(i) (alternate interior angles)
as AD || BC (produced)

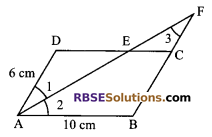
∠1 = ∠2 …(ii) (AF is the bisector of ∠A)
From (i) and (ii), we get
∠2 = ∠3
⇒ AB = BF (side opposite to equal angles are equal)
⇒ AB = BC + CF
⇒ 10 = 6 + CF
⇒ CF = 4 cm

Question 24.
P, Q, R and S are respectively, the mid-points of (RBSESolutions.com) the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD and AC ⊥ BD. Prove
that PQRS is a square.
Solution.
Given: ABCD is a quadrilateral and P, Q, R and S are the mid-points of the side AB, BC, CD and DA respectively, such that AC = BD and AC ⊥ BD

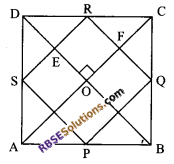
To prove: PQRS is a square.
Proof: Now, in ∆ADC, by mid-point theorem
SR || AC and SR = \(\frac { 1 }{ 2 }\) AC …(i)
In ∆ABC, by mid-point theorem
PQ || AC and PQ = \(\frac { 1 }{ 2 }\) AC …(ii)
From equation (i) and (ii), we get
PQ || SR and PQ = SR …(iii)
Now, in ∆ABD, by mid-point theorem
SP || BD and SP = \(\frac { 1 }{ 2 }\) BD = \(\frac { 1 }{ 2 }\) AC …(iv)
[∵ AC = BD (given)]
And, in ∆BCD, by mid-point theorem
RQ || BD and RQ = \(\frac { 1 }{ 2 }\) BD = \(\frac { 1 }{ 2 }\) AC …(v)
From equations (iv) and (v), we get
SP || RQ and SP = RQ = \(\frac { 1 }{ 2 }\) AC …(vi)
Now, from equations (iii) and (vi), we get
PQ = SR = SP = RQ
Thus, all four sides (RBSESolutions.com) are equal.
Now, in quadrilateral OERF
OE || FR and OF || ER
So, OERF is a parallelogram.
∆EOF = ∆ERF = 90° (opposite angles of a parallelogram)
and ∠QRS = 90°
Hence, PQRS is a square.
Hence proved.

Question 25.
A diagonal of a parallelogram bisects one (RBSESolutions.com) of its angle. Show that it is a rhombus.
Solution.
Given: ABCD is a parallelogram and diagonal AC bisects ∠A.

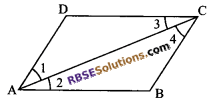
To prove: Diagonal AC bisects ∠A
∠1 = ∠2
Now, AB || CD and AC is a transversal.
∠2 = ∠3 (alternate interior angle)
Again AD || BC and AC is a transversal.
∠1 = ∠4 (alternate interior angles)
Now, ∠A = ∠C (opposite angles of a parallelogram)
⇒ \(\frac { 1 }{ 2 }\) ∠A = \(\frac { 1 }{ 2 }\) ∠C
⇒ ∠1 = ∠3
⇒ AD = CD (side opposite to equal angles)
AB = CD and AD = BC
AB = BC = CD = AD
⇒ ABCD is a rhombus.

Question 26.
ABCD is a quadrilateral in which AB || DC and AD = BC (see figure). Show that:
(i) ∠A = ∠B and
(ii) ∠C = ∠D
[Hint: Extend AB and draw (RBSESolutions.com) a line through C parallel to DA intersecting AB produced at E]

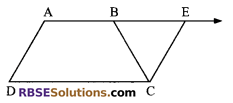
Solution.
Given: ABCD is a trapezium in which AB || CD and AD = BC.
To prove:
(i) ∠A = ∠B
(ii) ∠C = ∠D
Construction:
Join AC and BD. Extend line AB and draw (RBSESolutions.com) a line through C parallel to DA which meets AB produced at E.
Proof:
(i) AB || DC
⇒ AE || DC …(i)
and AD || CE …(ii) (by construction)
⇒ ADCE is a parallelogram
⇒ ∠A + ∠E = 180° …(iii) (sum of consecutive interior angles)
⇒ ∠ABC + ∠CBE = 180° …(iv) (linear pair of angles)
AD = CE …(v) (opposite sides of a parallelogram)
and AD = BC (given) …(vi)
⇒ BC = CE from (v) and (vi)
⇒ ∠CBE = ∠CEB …(vii) (angles opposite to equal sides)
⇒ ∠B + ∠E = 180° …(viii) [using (iv) and (vii)]
Now from (iii) and (viii), we have
∠A + ∠E = ∠B + ∠E
⇒ ∠A = ∠B
(ii) ∠A + ∠D = 180°
and ∠B + ∠C = 180°
⇒ ∠A + ∠D = ∠B + ∠C (∵ ∠A = ∠B)
⇒ ∠C = ∠D

Question 27.
In ∆ABC, AD is the median through A and E is the mid-point of AD. BE is produced (RBSESolutions.com) to meet AC in F. Prove that AF = \(\frac { 1 }{ 3 }\) AC.
Solution.
Given: ABC is a triangle in which AD is the median through A and E is the mid-point of AD.
To prove: AF = \(\frac { 1 }{ 3 }\) AC

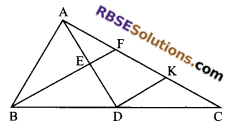
Construction: Through D, draw DK || BF
Proof: In ΔADK,
E is the mid-point of AD and EF || DK.
F is the mid-point of AK. (by converse of mid-point theorem)
⇒ AF = FK …(i)
In ΔBCF,
D is the mid-point of BC and DK || BF.
K is the mid-point of FC.
FK = KC …(ii)
From (i) and (ii), we get
AF = FK = KC …(iii)
Now, AC = AF + FK + KC
⇒ AC = AF + AF + AF [(using (iii)]
⇒ AC = 3AF
⇒ AF = \(\frac { 1 }{ 2 }\) AC.

Question 28.
Show that the line segment joining the mid-points (RBSESolutions.com) of the consecutive sides of a square is also of a square.
Solution.
Given: ABCD is a square in which E, F, G and H are respectively the mid-points of sides AB, BC, CD and DA.
To prove: EFGH is a square.
Construction: Join A to C and B to D.

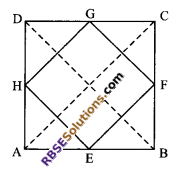
Proof: In ΔABC
E and F are mid-points of sides AB and BC.
From mid-point theorem
EF = \(\frac { 1 }{ 2 }\) AC …(i)
Similarly, HG = \(\frac { 1 }{ 2 }\) AC …(ii)
From (i) and (ii) EF = HG
Similarly, by joining B to D
We can say HE = GF
Since ABCD is a square
AB = BC = CD = DA
Again by using mid-point theorem
⇒ \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) DA
⇒ AE = AH
⇒ ∠AHE = ∠AEH = 45°
Similarly, ∠DHG = ∠DGH = 45°
∠AHE + ∠GHE + ∠DHG = 180°
⇒ 45° + ∠GHE + 45° = 180°
⇒ ∠GHE = 90°
⇒ EFGH is a square.

Question 29.
Show that the bisectors of the angles (RBSESolutions.com) of a parallelogram form a rectangle.
Solution.
Let ABCD be a parallelogram and P, Q, R and S be the points of intersection of the bisectors of ∠A and ∠D, ∠A and ∠B, ∠B and ∠C, ∠D and ∠C respectively of parallelogram ABCD.

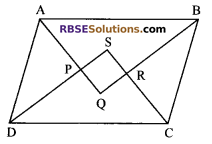
AP bisects ∠A and DP bisects ∠D. Therefore
∠DAP + ∠ADP = \(\frac { 1 }{ 2 }\) ∠A + \(\frac { 1 }{ 2 }\) ∠D
= \(\frac { 1 }{ 2 }\) (∠A + ∠D)
⇒ ∠DAP + ∠ADP = \(\frac { 1 }{ 2 }\) x 180° = 90° (sum of consecutive ∠s of a parallelogram)
∠DAP + ∠ADP = 90° ….(i)
Also in ∆ADP,
∠DAP + ∠ADP + ∠APD = 180° (angle sum property of a triangle)
⇒ 90° + ∠APD = 180°
⇒ ∠APD = 90° [using (ii)]
But ∠QPS = ∠APD (vertically opposite angles)
⇒ ∠QPS = 90° ..(ii)
Similarly, BR bisects ∠B and CR bisects,
∠C, therefore
∠QRS = 90° …(iii)
Also, AQ bisects ∠A and BQ bisects ∠B and DS bisects ∠D and CS bisects ∠C, therefore
∠PQR = 90° …(iv)
and ∠PSR = 90° ..(v)
So, using (ii), (iii), (iv) and (v), we can say that PQRS is (RBSESolutions.com) a quadrilateral in which all angles i.e. ∠P, ∠Q, ∠R and ∠S are right angles.
Hence, PQRS is a rectangle.

Question 30.
P and Q are points on opposite sides AD and BC of a parallelogram ABCD, such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
Solution.
Given: ABCD is a parallelogram, whose diagonals bisect each other at O, i.e. OB = OD and OC = OA.

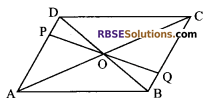
Proof: In ∆OBQ and ∆ODP
∠BOQ = ∠POD (vertically opposite angles)
∠OBQ = ∠ODP …(i) (since AD || BC and BD is transversal)
and OB = OD (given)
∆ODP = ∆OBQ (by ASA congruence rule)
Then, OP = OQ (by c.p.c.t)
Hence, O bisects PQ
Hence proved.

Question 31.
ABCD is a rectangle (RBSESolutions.com) whose diagonal BD bisects the ∠B. Show that ABCD is a square.
Solution.
Given: ABCD is a rectangle in which diagonal BD bisects ∠B
i.e. ∠1 = ∠2

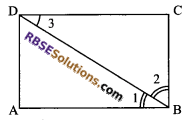
To prove: ABCD is a square.
Proof: In ∆ADB and ∆BDC
AB = DC (opposite sides of a rectangle)
∠1 = ∠3 (alternate angles)
and BD = BD (common)
∆ABD = ∆CDB (by SAS congruency rule)
But ∠1 = ∠2 (given)
⇒ ∠3 = ∠2
⇒ BC = DC (sides opposite to equal angles)
⇒ ABCD is a square.

Question 32.
D, E and F are respectively the mid-points (RBSESolutions.com) of the sides AB, BC and CA of a ∆ABC. Prove that by joining these mid-points D, E and F, the ∆ABC is divided into four congruent triangles.
Solution.
Given: ABC is a triangle and D, E and F are mid-points of sides AB, BC and CA, respectively.
To prove: ∆ABC is divided into four congruent triangles.
Construction: Join DE, EF and FD.

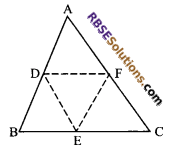
Proof: Given D, E and F are the mid-points (RBSESolutions.com) of sides AB, BC and CA respectively, then
AD = BD = \(\frac { 1 }{ 2 }\) AB
BE = EC = \(\frac { 1 }{ 2 }\) BC
and AF = CF = \(\frac { 1 }{ 2 }\) AC
Now, by mid-point theorem,
EF || AB
and EF = \(\frac { 1 }{ 2 }\) AB = AD = BD
ED || AC
and ED = \(\frac { 1 }{ 2 }\) AC = AF = CF
DF || BC
and DF = \(\frac { 1 }{ 2 }\) BC = BE = EC.
Now in ∆ADF and ∆EFD,
AD = EF (opposite sides of a parallelogram)
DF = FD (common sides)
and DE = AF
∆ADF = ∆EFD (by SSS congruence rule)
Similarly, ∆DEF = ∆DEB and ∆DEF = ∆CEF
Thus, ∆ABC is divided into four congruent triangles.
Hence proved.

Question 33.
In the given figure, ABCD is a trapezium in which AB || CD. M and N are mid-points (RBSESolutions.com) of the diagonal AC and BD respectively. Prove that MN || CD
and MN = \(\frac { 1 }{ 2 }\) (CD – AB)

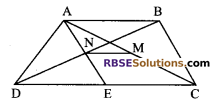
Solution.
Given: ABCD is a trapezium in which AB || CD and M and N are mid-points of diagonal AC and BD respectively.
Construction: Join AN and produce it to meet CD at E.
To prove: MN = \(\frac { 1 }{ 2 }\) (CD – AB)
and MN || CD
Proof: In ∆ANB and ∆END
∠ANB = ∠END (vertically opposite angles)
NB = ND (N is the mid-points of BD)
and ∠ABN = ∠EDN (alternate angles)
(∵ AB || CD and BD is a transversal)
∆ANB = ∆END (by ASA congruency rule)
⇒ AN = NE and AB = ED …(i) (by c.p.c.t)
Now in ∆EAC,
N and M are the mid-points of AE and AC respectively.
MN || EC and MN = \(\frac { 1 }{ 2 }\) EC (by mid-point theorem)
⇒ MN || EC
and MN = \(\frac { 1 }{ 2 }\) (CD – ED) = \(\frac { 1 }{ 2 }\) (CD – AB) [using (i)]
Hence, MN || CD (∵ MN || EC)
and MN = \(\frac { 1 }{ 2 }\) (CD – AB).

Question 34.
P is the mid-point of the side CD of (RBSESolutions.com) a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.

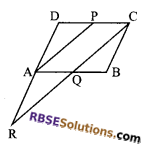
Solution.
Given: ABCD is a parallelogram (RBSESolutions.com) in which P is the mid-point of side CD.
To prove: DA = AR and CQ = QR
Proof: ABCD is a parallelogram.
BC = AD and BC || AD
Also, DC = AB and DC || AB
Since, P is mid-point of DC
DP = PC = \(\frac { 1 }{ 2 }\) DC
Now, QC || AP and PC || AQ.
Hence, APCQ is a parallelogram.
AQ = PC = \(\frac { 1 }{ 2 }\) DC = \(\frac { 1 }{ 2 }\) AB
= BQ [∵ DC = AB]
Now in ∆AQR and ∆BQC
AQ = BQ
∠AQR = ∠BQC (vertically opposite angles)
and ∠ARQ = ∠BCQ (alternate interior angles)
∆AQR = ∆BQC (by AAS congruence rule)
So, AR = BC (by c.p.c.t)
But, BC = DA
AR = DA
Also, CQ = QR (by c.p.c.t)
Hence proved.

Question 35.
Construct a quadrilateral ABCD, where AB = 3.7 cm, BC = 3 cm, CD = 5 cm, AD = 4 cm and ∠90°
Solution.
Steps of construction:

1. Draw a line segment AB = 3.7 m.
2. At A draw an angle of 90°.
3. By taking A as centre, draw (RBSESolutions.com) an arc of radius 4 cm which gives point D.
   
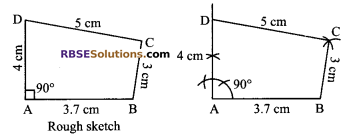
4. Again taking D as centre, draw an arc of 5 radius and from B draw an arc of 3 cm which intersect at C.
5. Join DC and BC.
   Hence, ABCD is the required quadrilateral.

Question 36.
Construct a quadrilateral ABCD in which AB = AD = 3.2 cm, BC = 2.5 cm, AC = 4 cm and BD = 5 cm.
Solution.
Steps of construction:

1. Draw AB = 3.2 cm.
2. With centre A, draw an arc of radius 3 cm and by taking B as centre take (RBSESolutions.com) an arc of 2.5 cm and cut the previous arc at C.
   
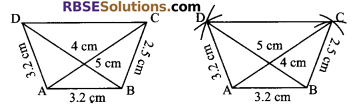
3. Further, take B as centre and draw an arc of 5 cm and cut an arc by 3.2 cm from A and mark that point as D.
4. Join C to D.
   Hence, ABCD is the required quadrilateral.

Question 37.
Construct a quadrilateral PQRS where PQ = 3.5 cm, QR = 3.5 cm, ∠P = 60°, ∠Q = 105° and ∠S = 75°.
Solution.
Steps of construction:

1. Draw PQ = 3.5 cm.
2. At P make an angle of 60° with (RBSESolutions.com) the help of compass.
   
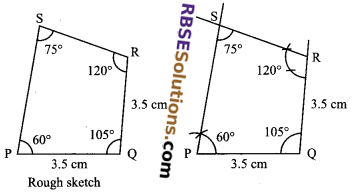
3. At Q draw the angle of 105° with the help of protractor. Again by taking Q as centre, draw an arc of 3.5 cm which intersects the line segment at R.
4. At R again draw an angle of 120°.
   i.e. 360° – (60° + 105° + 75°) = 360° – 240° = 120°
   which will intersect the arm of the angle 60° at S.
   Hence, PQRS is the required quadrilateral.

Question 38.
Construct a rhombus whose side is 3.6 cm and (RBSESolutions.com) one angle is 60°.
Solution.
Steps of construction:
As we know that in rhombus all sides are equal.

1. Draw base line AB = 3.6 cm.
   
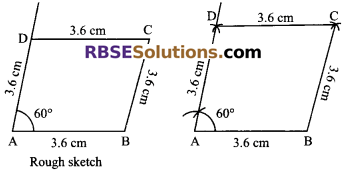
2. A draw an angle of 60° with the help of a compass.
3. By taking A as centre, cut an arc of 3.6 cm and mark it as D.
4. Again by taking D and B as centre, draw (RBSESolutions.com) an arc of 3.6 cm which intersects at the point C. Join BC, CD and DA.
   Hence, ABCD is the required rhombus.

Question 39.
Construct a square ABCD, where AB + BC + CD + DA = 12.8 cm
Solution.
AB + BC + CD + DA = 12.8 cm and AB = BC = CD = DA (∵ ABCD is a square)
Each side = \(\frac { 12.8 }{ 4 }\) = 3.2 cm.
Steps of construction:

1. Draw AB = 3.2 cm as base.
2. With centres A and B, draw an angle of 90° each.
   
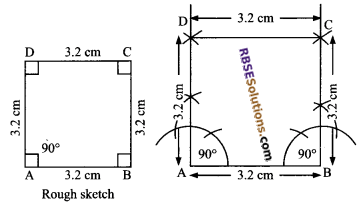
3. Taking A and B as centres, draw an arc 3.2 cm and cut it. Mark them as D and C.
4. Join D to C.
   Hence, ABCD is the required square.

Question 40.
Construct a trapezium ABCD in which AB || CD, AB = 5 cm, BC = 3 cm, AD = 3.3 cm and the (RBSESolutions.com) distance between the parallel sides is 2.5 cm.
Solution.
Steps of construction:

1. Draw a line segment XY.
2. Take any point E on it and draw a perpendicular on it.
3. With centre E, draw an arc of 2.5 cm and mark it as D.
   
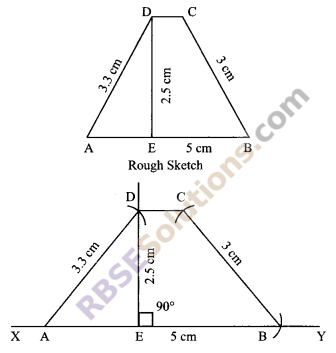
4. With centre D, draw an arc of 3.3 cm (RBSESolutions.com) which intersects XY at A.
5. Draw DC || AB, also draw an arc AB = 5 cm.
6. With centre B, draw an arc BC = 3 cm.
7. Join AD, CD and BC.
   Hence, ABCD is the required trapezium.

Question 41.
Construct a rhombus ABCD where AB = 6 cm and ∠A = 120°.
Solution.
Steps of construction:

1. As we know that in a rhombus (RBSESolutions.com) all sides are equal.
   
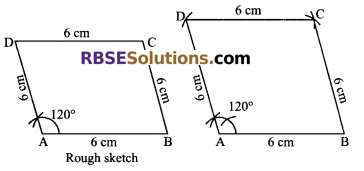
2. So first draw base AB = 6 cm. At a draw an angle of 120°, by taking A as centre, cut an arc of 6 cm and mark point D.
3. Again by taking B as centre, draw an arc of 6 cm which intersects at the point C. Join BC, CD and DA.
   Hence, ABCD is the required rhombus.

Question 42.
Construct a trapezium ABCD in which AB || CD, AB = 2.3, BC = 3.4 cm, CD = 5.4 cm and AD = 3.7 cm.
Solution.
Steps of construction:

1. Draw DC = 5.4 cm.
2. On DC mark a point E such that
   DE = DC – EC = 5.4 – 2.3 = 3.1 cm.
3. With centre C draw an arc of 3.4 cm.
4. With centre E draw an arc of 3.7 cm which (RBSESolutions.com) intersects the previous arc at B.
   
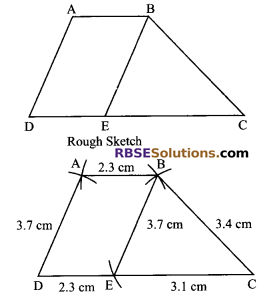
5. With centre B, draw an arc of 2.3 cm which intersects the line (RBSESolutions.com) segment which is coming through D.
6. Join AD, AB, BC and BE.
   Hence, ABCD is required trapezium.

Question 43.
Construct a rhombus the length of whose diagonals are 7.2 cm and 5.6 cm.
Solution.
Steps of construction:

1. Draw diagonal AC = 7.2 cm as base line.
2. Draw ⊥ bisector of AC which intersects AC at O.
3. Draw an arc of OD = OB = 2.8 cm above and below the ⊥ line (RBSESolutions.com) and marked them as D and B.
   
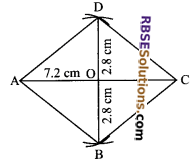
4. Join DA, DC, AB and BC.
   Hence, ABCD is the required rhombus.

Question 44.
Construct a rectangle ABCD in which AB = 4.5 and diagonal BD = 6 cm.
Solution.
Steps of construction:

1. Draw a line segment AB = 4.5 cm.
2. A draw an angle of 90°.
   
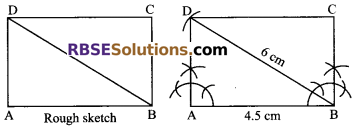
3. With centre B, draw an arc of 6 cm which cuts (RBSESolutions.com) the line segment of angle of 90° at D.
4. With centre D draw an arc of 6 cm.
5. At B draw an arc equal to AD.
   Hence, ABCD is the required rectangle.

We hope the given RBSE Solutions for Class 9 Maths Chapter 9 Quadrilaterals Miscellaneous Exercise will help you. If you have any query regarding RBSE Rajasthan Board Solutions for Class 9 Maths Chapter 9 Quadrilaterals Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.