RBSE Solutions for Class 10 Maths Chapter 16 पृष्ठीय क्षेत्रफल एवं आयतन Ex 16.3 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 16 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 16.3.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 16 |
| Chapter Name | पृष्ठीय क्षेत्रफल एवं आयतन |
| Exercise | Exercise 16.3 |
| Number of Questions Solved | 14 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 16 पृष्ठीय क्षेत्रफल एवं आयतन Ex 16.3
प्रश्न 1.
एक शंकु की ऊँचाई 28 सेमी. तथा आधार की त्रिज्या 21 सेमी. है। (RBSESolutions.com) उसका वक़ पृष्ठीय क्षेत्रफल, सम्पूर्ण पृष्ठीय क्षेत्रफल तथा आयतन ज्ञात कीजिए।
हल:
शंकु के आधार की त्रिज्या (r) = 21 सेमी.
शंकु की ऊँचाई (h) = 28 सेमी.
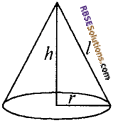
अतः शंकु की तिर्यक ऊँचाई
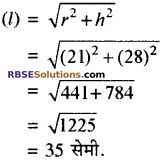
शंकु का वक्र पृष्ठीय क्षेत्रफल
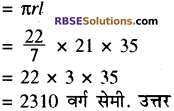
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल = πr (r + l)

![]()
प्रश्न 2.
एक लम्बवृत्तीय शंकु का आयतन 1232 सेमी3. है तथा उसकी ऊँचाई 24 सेमी. (RBSESolutions.com) है तो शंकु की तिरछी ऊँचाई ज्ञात कीजिए।
हल:
शंकु की ऊँचाई (h) = 24 सेमी.
माना शंकु के आधार की त्रिज्या r व तिर्यक ऊँचाई l है
शंकु का आयतन \(=\frac{1}{3} \pi r^{2} h=1232\) घन सेमी
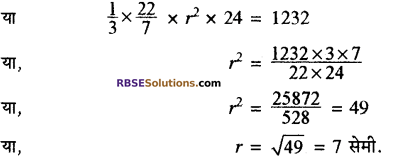
शंकु की तीर्थक ऊंचाई
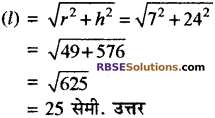
प्रश्न 3.
एक शंकु के आधार का व्यास 14 मीटर और तिर्यक ऊँचाई 25 मीटर है तो (RBSESolutions.com) शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
शंकु के आधार का व्यास = 14 मीटर
तब शंकु के आधार की त्रिज्या
![]()
शंकु की तिर्यक ऊँचाई (l) = 25 मीटर
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल = πr(r + l)
\(\begin{array}{l}{=\frac{22}{7} \times 7(7+25)} \\ {=22 \times 32}\end{array}\)
= 704 वर्गमीटर
अतः शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल = 704 वर्गमीटर उत्तर
प्रश्न 4.
शंकु के आधार की त्रिज्या 14 सेमी. और तिरछी ऊँचाई 50 सेमी. है। (RBSESolutions.com) शंकु का पृष्ठीय क्षेत्रफल (वक़ पृष्ठीय क्षेत्रफल), सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
शंकु के आधार की त्रिज्या (r) = 14 सेमी.
शंकु की तिर्यक ऊँचाई (l) = 50 सेमी.
शंकु का वक्र पृष्ठीय क्षेत्रफल = πrt
\(\begin{array}{l}{=\frac{22}{7} \times 14 \times 50} \\ {=22 \times 2 \times 50}\end{array}\)
= 2200 वर्ग सेमी. उत्तर
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल = πr(r + l)
\(\begin{array}{l}{=\frac{22}{7} \times 14 \times(14+50)} \\ {=22 \times 2 \times 64}\end{array}\)
= 2816 वर्ग सेमी, उत्तर
प्रश्न 5.
लम्ब वृत्तीय शंकु की ऊँचाई 8 सेमी. और आधार की त्रिज्या 6 सेमी. है। (RBSESolutions.com) उसका आयतन ज्ञात कीजिए।
हल:
शंकु की ऊँचाई (h) = 8 सेमी.
आधार की त्रिज्या (r) = 6 सेमी.
शंकु का आयतन =

प्रश्न 6.
एक शंकु का वक्र पृष्ठीय क्षेत्रफल 1884.4 मीटर है तथा इसकी तिर्यक ऊँचाई 12 मीटर है। (RBSESolutions.com) इसके आधार की त्रिज्या ज्ञात कीजिए।
हल:
शंकु की तिर्यक ऊँचाई (l) = 12 मीटर
माना इसके आधार की त्रिज्या = r है।
दिया है-शंकु का वक्र पृष्ठीय क्षेत्रफल = 1884.4 मीटर
πrl = 1884.4

![]()
प्रश्न 7.
एक लम्ब वृत्तीय शंकु के आधार का क्षेत्रफल 154 cm2 है। (RBSESolutions.com) इसकी तिरछी ऊँचाई 25 सेमी. है तो शंकु की ऊँचाई ज्ञात कीजिए।
हल:
शंकु की तिर्यक ऊँचाई (l) = 25 सेमी.
माना शंकु की ऊँचाई = h सेमी.
शंकु के आधार का क्षेत्रफल = 154 सेमी2.
यदि शंकु के आधार की त्रिज्या r सेमी. है तब
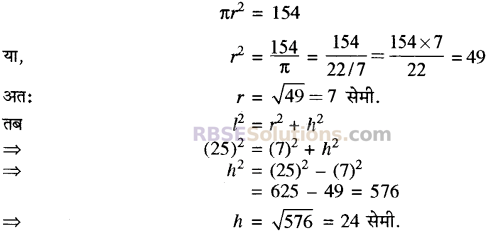
अतः शंकु की ऊँचाई = 24 सेमी. उत्तर
प्रश्न 8.
दो शंकुओं के आधार का व्यास समान है। उनकी तिर्यक ऊँचाइयों का अनुपात 5 : 4 है। (RBSESolutions.com) यदि छोटे शंकु का वक्र पृष्ठीय क्षेत्रफल 400 सेमी. है, तो बड़े शंकु का वक़ पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
दोनों शंकुओं के आधार का व्यास समान है अतः त्रिज्या भी समान होगी
माना छोटे शंकु की तिरछी ऊँचाई l1 है तथा बड़े शंकु की तिरछी ऊँचाई l2 है।
बड़े तथा छोटे शंकु की तिरछी ऊँचाइयों का अनुपा \(=\frac{l_{1}}{l_{2}}=\frac{5}{4}\)
छोटे शंकु के वक्रपृष्ठ का क्षेत्रफल = πrl2 = 400 सेमी2
बड़े शंकु के वक्रपृष्ठ का क्षेत्रफल = πrl1 होगा।


प्रश्न 9.
एक शंकु की तिर्यक ऊँचाई और त्रिज्या का अनुपात 7: 4 है। (RBSESolutions.com) यदि इसके वक्रपृष्ठ का क्षेत्रफल 792 वर्ग सेमी. हो, तो इसकी त्रिज्या ज्ञात कीजिए।
हल:
शंकु की तिर्यक ऊँचाई व त्रिज्या को अनुपात = 7: 4

प्रश्नानुसार शंकु के वक्रपृष्ठ का क्षेत्रफल = πrl

अर्थात् इसकी त्रिज्या 12 सेमी. है।
अतः शंकु की त्रिज्या = 12 सेमी. उत्तर
प्रश्न 10.
9 मीटर ऊँचे शंकु के आकार के टेन्ट के आधार की परिधि 44 मीटर है। (RBSESolutions.com) इसके अन्दर की वायु का आयतन ज्ञात कीजिए।
हल:
तंबू के आधार की परिधि 2πr = 44 मी.
आधार की त्रिज्या
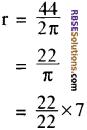
7 मी.
शंकु की ऊँचाई h = 9 मीटर
शंकु के अन्दर की वायु का आयतन
\(\begin{array}{l}{=\frac{1}{3} \pi r^{2} h} \\ {=\frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 9} \\ {=22 \times 7 \times 3}\end{array}\)
= 462 मी3. उत्तर
प्रश्न 11.
एक शंकु के आकार के बर्तन की त्रिज्या 10 सेमी. और ऊँचाई 18 सेमी. है। (RBSESolutions.com) यह पानी से पूरा भरा हुआ है। इसे 5 सेमी. त्रिज्या के एक बेलनाकार बर्तन में उँडेला जाता है। बेलनाकार बर्तन में पानी की ऊँचाई ज्ञात कीजिए।
हल:
शंकु के आकार के बर्तन की त्रिज्या (r) = 10 सेमी.
ऊँचाई (h) = 18 सेमी.
शंकु का आयतन
\(\begin{array}{l}{=\frac{1}{3} \pi r^{2} h} \\ {=\frac{1}{3} \times \pi \times 10 \times 10 \times 18}\end{array}\) घन सेमी.
= π × 100 × 6 घन सेमी.
= 600 π घन सेमी.
∴ इस आयतन के पानी को बेलनाकार बर्तन में डाला जाता है।
∴ बेलन का आयतन = πr2h अर्थात्
πr2h = 600
\(\begin{aligned} \mathrm{h} &=\frac{600 \pi}{\pi \times 5 \times 5} \\ \mathrm{h} &=\frac{600}{25}=24 \end{aligned}\) सेमी.
∴ बेलनाकार बर्तन में पानी की ऊँचाई 24 सेमी. होगी। उत्तर
![]()
प्रश्न 12.
14 सेमी. भुजा के एक घन से बड़े से बड़ा शंकु काटा जाता है। (RBSESolutions.com) शंकु का आयतन ज्ञात कीजिए।
हल:
14 सेमी. भुजा वाले घन से बड़े से बड़ा शंकु काटकर निकालने के लिए उसके आधार की त्रिज्या होगी।
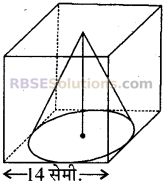
![]()
और शंकु की ऊँचाई = भुजा = 14 सेमी.
अतः शंकु का अभीष्ट आयतन \(=\frac{1}{3} \pi r^{2} h\)

प्रश्न 13.
शंकु के आधार की त्रिज्या और ऊँचाई क्रमशः 7 सेमी. और 24 सेमी. है। (RBSESolutions.com) शंकु की तिरछी ऊँचाई, वक़पृष्ठ का क्षेत्रफल, सम्पूर्ण पृष्ठीय क्षेत्रफल एवं आयतन ज्ञात कीजिए।
हल:
शंकु के आधार की त्रिज्या (r) = 7 सेमी.
ऊँचाई (h) = 24 सेमी.
- ∴ शंकु की तिर्यक ऊँचाई

- शंकु के वक्रपृष्ठ का क्षेत्रफल

- शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल

- शंकु का आयतन

प्रश्न 14.
एक त्रिज्यखण्ड की त्रिज्या 12 सेमी. और कोण 120° है। (RBSESolutions.com) इसकी सीधी कोरों को संपाती करके एक शंकु बनाया जाता है। इस शंकु का आयतन ज्ञात कीजिए।
हल:
प्रश्नानुसार त्रिज्यखण्ड के चाप AB की लंबाई
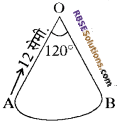
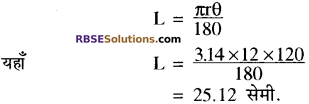
यदि त्रिज्यखण्ड AOB को काटकर एवं सीधी कोरों को मिलायें तो (RBSESolutions.com) प्राप्त शंकु के लिए AO = l = तिर्यक ऊँचाई बन जायेगी। अर्थात् l = AO = 12 सेमी. तथा चाप AB शंकु के लिए आधार वृत्त बन जायेगा जिसकी त्रिज्या माना R है।

![]()
We hope the RBSE Solutions for Class 10 Maths Chapter 16 पृष्ठीय क्षेत्रफल एवं आयतन Ex 16.3 help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 16 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 16.3, drop a comment below and we will get back to you at the earliest.