RBSE Solutions for Class 10 Maths Chapter 7 त्रिकोणमितीय सर्वसमिकाएँ Ex 7.2

RBSE Solutions for Class 10 Maths Chapter 7 त्रिकोणमितीय सर्वसमिकाएँ Ex 7.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 7 त्रिकोणमितीय सर्वसमिकाएँ Exercise 7.2.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 10
Subject	Maths
Chapter	Chapter 7
Chapter Name	त्रिकोणमितीय सर्वसमिकाएँ
Exercise	Exercise 7.2
Number of Questions Solved	18
Category	RBSE Solutions

Rajasthan Board RBSE Class 10 Maths Chapter 7 त्रिकोणमितीय सर्वसमिकाएँ Ex 7.2

निम्नलिखित के मान ज्ञात करो-

प्रश्न 1.

हल:

प्रश्न 2.
(i) cosec 25° – sec 65°
(ii) cot 34° – tan 56° (RBSESolutions.com)
(iii) \(\frac{\sin 36^{\circ}}{\cos 54^{\circ}}-\frac{\sin 54^{\circ}}{\cos 36^{\circ}}\)
(iv) sin θ cos(90° – θ) + cos θ sin(90° – θ)
हल:
(i) cosec 25° – sec 65°
= cosec(90° – 65°) – sec 65° [∵ cosec(90° – θ) = sec θ]
= sec 65° – sec 65°
= 0 उत्तर

(ii) cot 34° – tan 56° .
= cot (90° – 56°) – tan 56° [∵ cot(90° – θ) = tan θ]
= tan 56° – tan 56°
= 0 उत्तर

(iv) sin θ cos(90° – θ) + cos θ sin(90° – θ) [∵ cos(90° – θ) = sin θ sin(90° – θ) = cos θ]
= sin θ . sin θ + cos θ . cos θ
= sin²θ + cos²θ [∵ sin² θ = cos² θ = 1]
= 1 उत्तर

प्रश्न 3.
(i) sin 70° sec 20° – cos 20° cosec 70°
(ii) \(\frac{2 \cos 67^{\circ}}{\sin 23^{\circ}}-\frac{\tan 40^{\circ}}{\cot 50^{\circ}}-\cos 60^{\circ}\)
हल:
(i) sin 70° sec 20° – cos 20° cosec 70° (RBSESolutions.com)
= sin 70° . sec (90° – 70°) – cos 20° . cosec(90° – 20°) [∵ sec(90° – θ) = cosec θ और cosec(90° – θ0) = sec θ]
= sin 70° cosec 70° – cos 20° sec 20°
\(\begin{array}{l}{=\sin 70^{\circ} \cdot \frac{1}{\sin 70^{\circ}}-\cos 20^{\circ} \cdot \frac{1}{\cos 20^{\circ}}} \\ {=\frac{\sin 70^{\circ}}{\sin 70^{\circ}}-\frac{\cos 20^{\circ}}{\cos 20^{\circ}}}\end{array}\)
= 1 – 1 उत्तर

प्रश्न 4.

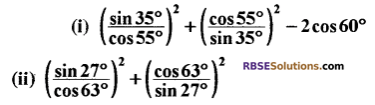
हल:

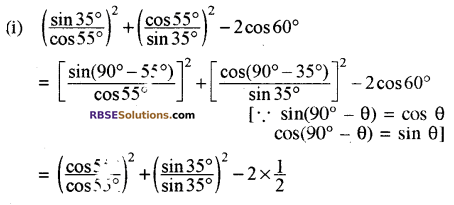
प्रश्न 5.
(i) cot 12° cot 38° cot 52° cot 60° cot 78°
(ii) tan 5° tan 25° tan 30° tan 65° tan 85°
हल:
(i) cot 12° cot 38° cot 52° cot 60° cot 78° (RBSESolutions.com)
= cot 12° cot 78° cot 38° cot 52° cot 60°
= cot (90° – 78°). cot 78° . cot (90° – 52°) . cot 52° . cot 60° ∵ cot(90° – θ) = tan θ
= tan 78°. cot 78° . tan 52°. cot 52°. \(\frac{1}{\sqrt{3}}\)
= tan 78° . tan 78° . tan 52° . \(\frac{1}{\tan 52^{\circ}} \cdot \frac{1}{\sqrt{3}}\)
1 . 1 . \(\frac{1}{\sqrt{3}}=\frac{1}{\sqrt{3}}\) उत्तर

(ii) tan 5° tan 25° tan 30° tan 65° tan 85°
= tan 5° . tan 25° . tan 65°. tan 85° . tan 30°
= tan 5° tan 85° . tan 25° tan 65o° . tan 30°
= tan(90° – 85°) tan 85° , tan (90° – 65°) tan 65°. \(\frac{1}{\sqrt{3}}\)
∵ tan(90° – θ) = cot θ
= cot 85° tan 85°. cot 65o tan 65° . \(\frac{1}{\sqrt{3}}\)
\(=\frac{1}{\tan 85^{\circ}} \times \tan 85^{\circ} \cdot \frac{1}{\tan 65^{\circ}} \times \tan 65^{\circ} \cdot \frac{1}{\sqrt{3}}\)
1 . 1 . \(\frac{1}{\sqrt{3}}=\frac{1}{\sqrt{3}}\) उत्तर

प्रश्न 6.
निम्न को 0° से 45° के कोणों के त्रिकोणमितीय अनुपातों के (RBSESolutions.com) पदों में व्यक्त कीजिए
(i) sin 81° + sin 71°
(ii) tan 68° + sec 68°
हल:
(i) sin 81° + sin 71°
∵ 81°= 90° – 9°
∴ sin 81°= sin (90° – 9°).
∵ sin(90° – θ) = Cos θ
तथा = cos 9° …..(i)
71°= 90° – 19°
sin 71°= sin (90° – 19°)
∵ sin(90° – θ) = cos θ sin 71°
= cos 19° …..(ii)
(i) व (ii) से मान दिए गए व्यंजक (RBSESolutions.com) में रखने पर
= sin 81° + sin 71°
= cos 9° + cos 19° उत्तर

(ii) tan 68° + sec 68°
68°= 90° – 22°
tan 68° = tan(90° – 22°)
∵ tan(90° – θ) = cot θ
∴ tan 68°= cot 22° …..(i)
पुन: 68°= 90° – 22°
sec 68° = sec (90° – 22°)
sec(90° – θ) = cotθ
या sec 68° = cosec 22° …..(ii)
(i) व (ii) से मान दिए गए व्यंजक में रखने पर
tan 68° + sec 68° = cot 22° + cosec 22° उत्तर

निम्नलिखित को सिद्ध कीजिए-

प्रश्न 7.
sin 65° + c0s 25° = 2 cos 25°
हल:
L.H.S. = sin 65° + cos 25°
∵ 65°= 90° – 25°
∴ sin 65°= sin (90° – 25°) [∵ sin(90° – θ) = cos θ]
या
sin 65° = cos 25°
मान व्यंजक में रखने पर
= sin 65° + cos 25°
= cos 25° + cos 25°
= 2 cos 25° = R.H.S.
∴ L.H.S. = R.H.S. ( इतिसिद्धम् ) (RBSESolutions.com)

प्रश्न 8.
sin 35° sin 55° – cos 35° cos 55° = 0
हल:
L.H.S. = sin 35° sin 55° – cos 35° cos 55°
= sin 35° sin (90°-35°) – cos 35° . cos (90°-35°)
[∵ sin(90° – θ) = cos θ
cos(90° – θ) = sin θ]
= sin 35°. cos 35° – cos 35°. sin 35°
= sin 35° (cos 35° – cos 35°)
= sin 35°. 0 = 0 = R.H.S. ( इतिसिद्धम् )
∴ L.H.S. = R.H.S.

प्रश्न 9.
\(\frac{\cos 70^{\circ}}{\sin 20^{\circ}}+\frac{\cos 59^{\circ}}{\sin 31^{\circ}}-8 \sin ^{2} 30^{\circ}=0\)
हल:

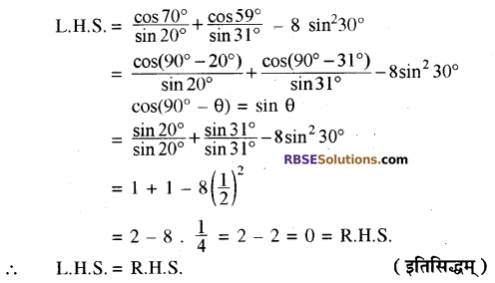
प्रश्न 10.
sin (90° – θ) cos (90° – θ) = \(\frac{\tan \theta}{1+\tan ^{2} \theta}\)
हल:
L.H.S. = sin(90° – θ) cos(90° – θ)
= cos θ . sin θ = sin θ cos θ …..(1)

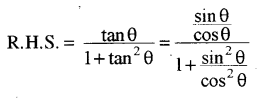
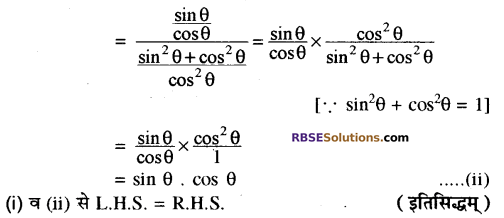
प्रश्न 11.
\(\frac{\cos \left(90^{\circ}-\theta\right) \cos \theta}{\tan \theta}\) + cos²(90° – θ) = 1
हल:

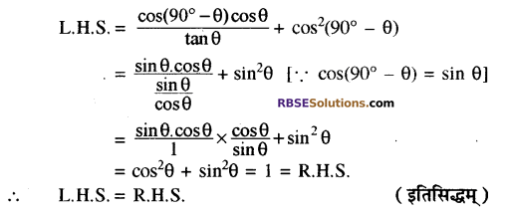
प्रश्न 12.

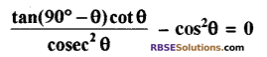
हल:

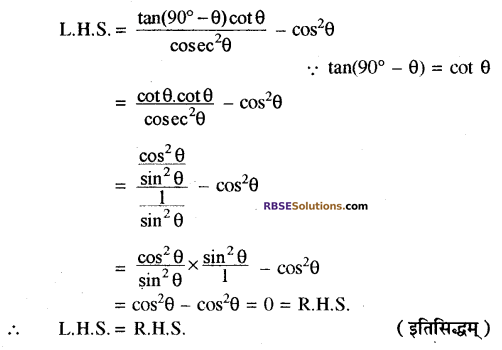
प्रश्न 13.
\(\frac{\cos \left(90^{\circ}-\theta\right) \sin \left(90^{\circ}-\theta\right)}{\tan \left(90^{\circ}-\theta\right)}\) = sin²θ
हल:

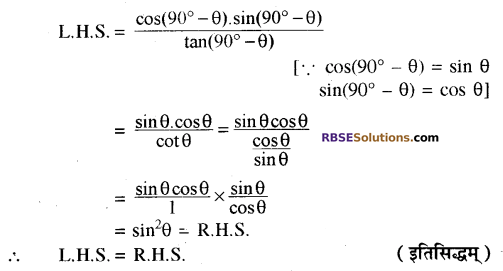
प्रश्न 14.

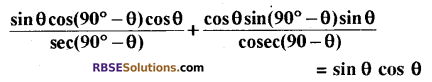
हल:

प्रश्न 15.
यदि sin 3θ = cos (θ – 6°) यहाँ 3θ और (θ – 6°) न्यूनकोण है (RBSESolutions.com) तो θ का मान ज्ञात कीजिए।
हल:
यहाँ दिया हुआ है की sin 3θ = cos (θ – 6°) …(i)
∵ sin 3θ = cos(90° – 3θ)
∴ समीकरण (i) को इस रूप में लिख सकते हैं-
cos(90° – 3θ) = cos(θ – 6°)
क्योंकि 90° – 3θ और θ – 6° दोनों ही न्यूनकोण हैं, इसलिए
90° – 3θ = θ – 6°
या -3θ – θ = – 6° – 90°
या -4θ = – 96°
जिससे \(\theta=\frac{-96^{\circ}}{-4}=24^{\circ}\)
अतः θ का मान 24° होगा। उत्तर

प्रश्न 16.
यदि sec 5θ = cosec (θ – 36°) यहाँ 58 एक न्यूनकोण है। (RBSESolutions.com) तो θ का मान ज्ञात कीजिए।
हल:
प्रश्नानुसार दिया गया है कि sec 5θ = cosec (θ – 36°) …..(i)
∵ sec 5θ = cosec (90° – 5θ)
∴ समीकरण (i) को इस रूप में भी लिखा जा सकता है
cosec(90° – 5θ) = cosec(θ – 36°)
क्योंकि 90° – 5θ और θ – 36° दोनों ही न्यूनकोण हैं,
∴ 90° – 5θ = θ – 36°
या – 5θ – θ = – 36° – 90°
या – 6θ = – 126°
∴ \(\theta=\frac{-126}{-6}=21^{\circ}\)
अतः 8 का मान 21° होगा। उत्तर

प्रश्न 17.
यदि A, B और C किसी त्रिभुज ABC के अन्त:कोण हों तो सिद्ध (RBSESolutions.com) कीजिए कि \(\tan \left(\frac{B+C}{2}\right)=\cot \frac{A}{2}\)
हल:
A, B और C त्रिभुज के अन्त:कोण हैं।
∴ A + B + C = 180° [त्रिभुज के तीनों कोणों का जोड़ 180° होता है]

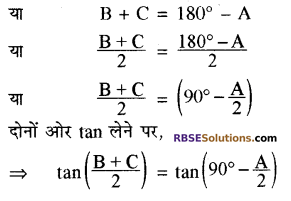
\(=\cot \frac{\mathbf{A}}{2}\)
[∵ tan (90° – θ) = cot ] इतिसिद्धम्।

प्रश्न 18.
यदि cos 2θ = sin 4θ हो और 2θ व 4θ न्यूनकोण हो (RBSESolutions.com) तो θ का मान ज्ञात कीजिए।
हल:
प्रश्नानुसार दिया गया है कि cos 2θ = sin 4θ …..(i)
∵ cos 2θ8 = sin(90° – 2θ)
∴ समीकरण (i) को इस रूप में भी लिखा जा सकता है-
sin(90° – 2θ) = sin 4θ
क्योंकि 90° – 2θ और 4θ दोनों ही न्यूनकोण हैं।
∴ 90° – 2θ = 4θ
या – 2θ – 4θ = – 90°
या – 6θ = – 9θ°
∴ \(\theta=\frac{-90^{\circ}}{-6}=15^{\circ}\)
अतः θ का मान 15° होगा। उत्तर

We hope the RBSE Solutions for Class 10 Maths Chapter 7 त्रिकोणमितीय सर्वसमिकाएँ Ex 7.2 help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 7 त्रिकोणमितीय सर्वसमिकाएँ Exercise 7.2, drop a comment below and we will get back to you at the earliest.