RBSE Solutions for Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise

RBSE Solutions for Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise.

Rajasthan Board RBSE Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise

Question 1.
The shadow of a vertical pillar is (RBSESolutions.com) same the height of pillar, then angle of elevation of sun will be :
(A) 45°
(B) 30°
(C) 60°
(D) 50°
Solution :
Let BC is a tower with height h. Then according to question its shadow AB will be h m.

Let angle of elevation = θ
In right angled ΔABC, (RBSESolutions.com) we have
tan θ = \(\frac { BC }{ AB }\) = \(\frac { h }{ h }\) = 1
or tan θ = tan 45°
or θ = tan 45°
Hence, correct choice is (A).

Question 2.
From a point on the ground which is 100 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°, then height of tower is :
(A) 100 √3 m
(B) \(\frac { 100 }{ \sqrt { 3 } }\) m
(C) 50 √3 m
(D) \(\frac { 200 }{ \sqrt { 3 } }\) m
Solution :
Let BC is a tower with height h and angle (RBSESolutions.com) of elevation is 60° from point A which is 100 m far from tower with base B. So ∠CAB = 60°
In right angled ∆ABC,

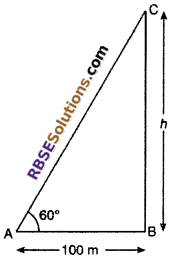
tan 60° = \(\frac { BC }{ AB }\)
⇒ \(\sqrt { 3 }\) = \(\frac { h }{ 100 }\)
So, correct choice is (A)

Question 3.
A 15 m long ladder touches the top (RBSESolutions.com) of a vertical wall. If this ladder makes an angle of 60° with the wall, then height of the wall is : (CBSE 2013)
(A) 15 √3 m
(B) \(\frac { 15\sqrt { 3 } }{ 2 }\) m
(C) \(\frac { 15 }{ 2 }\) m
(D) 15 m
Solution :
Let AB is vertical wall with height h. Let AC is a ladder with length 15 m. Ladder makes an angle 60° from the wall, then ∠ACB = 60°

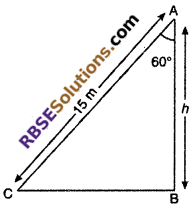
From right angled ΔABC
cos 60° = \(\frac { h }{ 15 }\)
⇒ \(\frac { 1 }{ 2 }\) = \(\frac { h }{ 15 }\) ⇒ h = \(\frac { 15 }{ 2 }\) m
Hence, correct choice is (C).

Question 4.
From the top of a loom height tower, (RBSESolutions.com) angle of depression at a point on earth is 30°. Distance of point from base of tower is
(A) 10√3 m
(B) \(\frac { 10 }{ \sqrt { 3 } }\) m
(C) 10 m
(D) 5√3 m
Solution :
Let BC is a tower with height 10 m. Let the distance of point A from the base of the tower AB = x m and angle of depression is 30° of point A from the top of tower.
Hence, ∠CAB = 30°

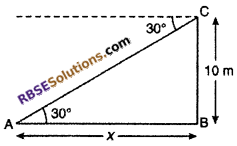
From right angled ∆ABC
tan 30° = \(\frac { BC }{ AB }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { 10 }{ x }\) ⇒ x = 10√3 m
Hence, correct choice is (A).

Question 5.
A bridge above the river makes an angle (RBSESolutions.com) of 45° with the bank of river. If length of bridge above the river is 150 m, then breadth of river will be :
(A) 75 m
(B) 50√2 m
(C) 150 m
(D) 75√2 m
Solution :
Let AC is a bridge with its length 150 m and BC is a breadth of river. Bridge makes an angle 45° with the river i.e.,
∠CAB = 45°
From right angled ∆ABC
sin 45° = \(\frac { BC }{ AC }\)

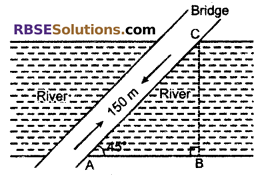
⇒ \(\frac { 1 }{ \sqrt { 2 } }\) = \(\frac { BC }{ 150 }\)

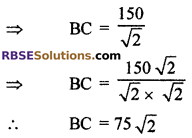
Hence, breadth of river 75√2 m
Hence, the correct choice is (D)

Question 6.
Top of two towers of height 20 m and 14 m are (RBSESolutions.com) joined by a wire. If wire make an angle of 30° with horizontal line then length of wire is :
(A) 12 m
(B) 10 m
(C) 8 m
(D) 6 m
Solution :
Let two towers are AE and BD where BD = 20 m and AE = 14 m. Let ED is a wire which makes an angle of 30° horizontal line. So

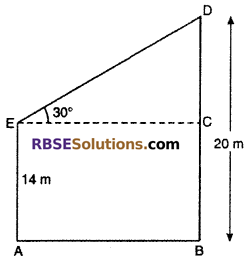
∠DEC = 30°
BD = BC + DC
BD = AE + DC
20 = 14 + DC
DC = 20 – 14 = 6 m
From right angled ∆ECD
sin 30° = \(\frac { CD }{ ED }\)
⇒ \(\frac { 1 }{ 2 }\) = \(\frac { 6 }{ ED }\)
⇒ ED = 6 × 2 = 12 m
Hence, the correct choice is (A).

Question 7.
The angle of elevations of the top of the tower (RBSESolutions.com) from two points distance a and b from the base of tower (a > b) and 30° and 60° then height of tower is :
(A) \(\sqrt { a+b }\)
(B) \(\sqrt { a-b }\)
(C) \(\sqrt { ab }\)
(D) \(\sqrt { \frac { a }{ b } }\)
Solution :

Let CD is a tower with its height h. Let b is the distance of point B from the base of tower C and a is a distance of point A.
So, ∠CAD = 30°, ∠CBD = 60°
From right angled ∆ACD,
tan 30° = \(\frac { h }{ ac }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { h }{ a }\)
⇒ h = \(\frac { a }{ \sqrt { 3 } }\) …..(i)
From right angled ∆BCD,
tan 60° = \(\frac { h }{ b }\)
⇒ \(\sqrt { 3 }\) = \(\frac { h }{ b }\) …(ii)
⇒ h = √3b
From equation (i) and (ii),
h² = ab
or h = \(\sqrt { ab }\)
So, correct choice is (C).

Question 8.
From the top of a 25 m high pillar at the top of tower angle (RBSESolutions.com) of elevation is same as the angle of depression of foot of tower then height of tower is :
(A) 25 m
(B) 100 m
(C) 75 m
(D) 50 m
Solution :
Let AE is a pillar in the figure with height 25 m and BD is a tower. According to question at the top of tower angle of elevation is same as the angle of depression of foot of tower.

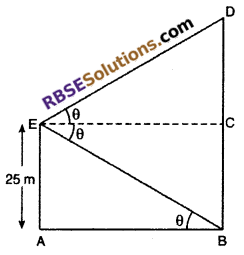
So ∠CED = ∠CEB = ∠ABE = θ
and AE = BC = 2 m
From right angled ΔBAE
tan θ = \(\frac { 25 }{ AB }\)
or AB = \(\frac { 25 }{ tan\theta } \) = 25 cotθ
From right angled ΔECD,
tan θ = \(\frac { CD }{ EC }\) = \(\frac { CD }{ AB }\)
tan θ = \(\frac { CD }{ 25cot\theta }\)
or CD = 25 cot θ × tan θ
= 25 m [∵ tan θ cot θ = 1]
Hence, height of tower = BC + CD
= 25 + 25
= 50 m
So, correct choice is (D).

Question 9.
If ratio of length of a vertical rod and length of (RBSESolutions.com) its shadow is 1 : √3, then angle of elevation of sun is :
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Solution :
Let length of vertical rod is BC and length of shadow is AB.
Let angle of elevation of sun is θ then,

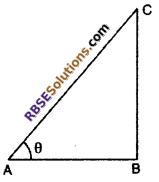
From right ΔABC,
tan θ = \(\frac { BC }{ AB }\)
= \(\frac { 1 }{ \sqrt { 3 } }\) = tan 30°
or θ = 30°
Hence, angle of elevation of sun = 30°
So, correct choice is (A).

Question 10.
The slope of a hill makes an angle of 60° with (RBSESolutions.com) horizontal axis. If to reach at top, 500 m distance have to covered then height of the hill is :
(A) 500√3 m
(B) \(\frac { 500 }{ \sqrt { 3 } }\) m
(C) 250√3 m
(D) \(\frac { 250 }{ \sqrt { 3 } }\) m
Solution :
Let height of hill BC = h m
Let slope of hill makes an angle 60° with point A and AC = 500 m and ∠BAC = 60°,

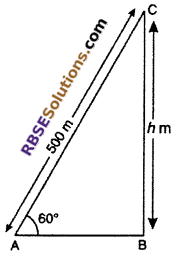
From right angled ∆ABC
sin 60° = \(\frac { BC }{ AC }\)
\(\frac { \sqrt { 3 } }{ 2 } \) = \(\frac { h }{ 500 }\)
h = \(\frac { 500\sqrt { 3 } }{ 2 }\)
= 250√3
Hence, correct choice is (C).

Question 11.
A tower is vertically placed on a horizontal plane. (RBSESolutions.com) If angle of elevation of sun is 30 and length of shadow of tower is 45 m, then find height of the tower.
Solution :
Let height of tower is h and length of shadow of tower AB is 45 m. The angle of elevation of sun is 30°.

From right angled ∆ABC
tan 30° = \(\frac { BC }{ AB }\)
\(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { h }{ 45 }\)

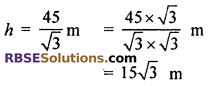
Hence, height of tower is 15√3 m

Question 12.
The upper part of a tree is broken by windstorm (RBSESolutions.com) and it makes an angle of 60° with the ground. The distance from the bottom of the tree to the point where the top touches the ground is 10 m. Find the original height of the tree. (√3 = 1.732)
Solution :
Let length of tree before windstorm is BD.
After windstorm the upper part of tree C falls from point C to point A on the ground.
Now, let CD = AC = h₂ m
AB = 10 m
Broken part makes an angle 60° from the ground.

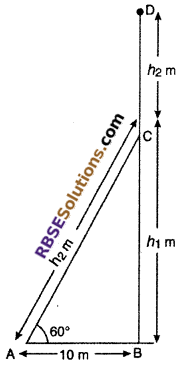
So, ∠CAB = 60°
From right angled ∆ABC
tan 60° = \(\frac { BC }{ AB }\)
⇒ √3 = \(\frac { { h }_{ 1 } }{ 10 }\)
⇒ h₁ = 10√3
and cos 60° = \(\frac { AB }{ AC }\)
⇒ \(\frac { 1 }{ 2 }\) = \(\frac { { 10 } }{ { h }_{ 2 } }\)
⇒ h₂ = 10 × 2
= 20 m
Hence, total length of tree
BD = BC + CD
= h₁ + h₁
= 10√3 + 20
= 10 × 1.732 + 20
= 17.32 + 20
= 37.32 m
Hence, height of the tree 37.32 m

Question 13.
From a point on the ground which is 120 m (RBSESolutions.com) away from the foot of the unfinished tower, the angle of elevation of the top of the tower is found to be 30° find how much height of tower have to increased so that its angle of elevation at same point became 60°?
Solution :
Let BC is a incomplete tower with height h₁. Point A is 120 m distance from its base B, the angle of elevation is 30° from its top, i.e., ∠BAC = 30°.
Let the tower be given height h₂ m till point D. So that angle of elevation becomes 60° from point A.

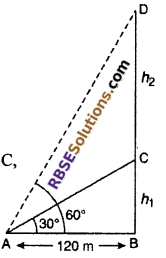
∠BAD = 60°
From right angled ∆ABC,

From right angled ∆ABD,
tan 60° = \(\frac { BD }{ AB }\)
\(\sqrt { 3 }\) = \(\frac { { h }_{ 1 }+{ h }_{ 2 } }{ 120 }\)
h₁ + h₂ = 120√3
40√3 + h₂ = 120√3
h₂ = 120√3 – 40√3
= 80√3 m
= 80 × 1.732
CD = 138.56 m
Hence, 138.56 m height of tower (RBSESolutions.com) have to be increased.

Question 14.
The angle of elevation of the top of a tower from a point situated at 100 m far from the foot of tower is 300. Find the height of the tower.
Solution :
Let height of tower BC = h meter and angle of elevation is 30° from point A which is 100 m from the base B of tower then

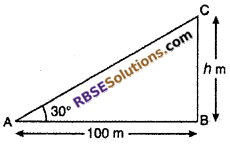
∠BAC = 30°
From right angled ∆ABC,

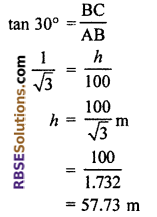
Hence, height of the tower 57.73 m

Question 15.
The angle of elevation of the top of a pillar (RBSESolutions.com) from a point on the ground is 15° on walking 100 m towards the tower, the angle of elevation is found to be 30°. Calculate the height of the tower (where tan 15 = 2 – √3).
Solution :
Let CD is a pillar of height h m. The angle of elevation of its top at A be 15°. Let B be a point at a distance of 100 m from A such that the angle of elevation of the top of the tower at B be 30°.
Let BC = x m, so ∠DAC = 15°, ∠DBC = 30°, AB = 100 m

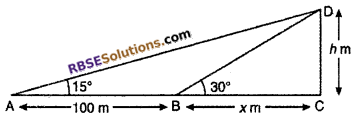
From right angled ∆BCD,
tan 30° = \(\frac { CD }{ BC }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { h }{ x }\)
⇒ x = h√3 m
From right angled ∆ACD,

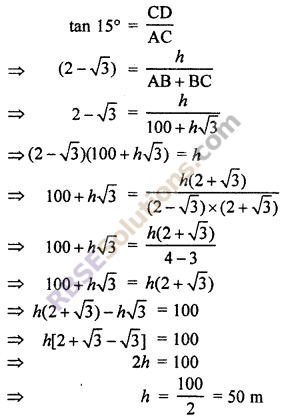
Hence, height of pillar is 50 m

Question 16.
The shadow of a vertical tower on level (RBSESolutions.com) ground is increased by 40 m, when the altitude of the sun changes from 60° to 30°. Find the height of the tower.
Solution :
Let CD is a tower of height h. Let from its base C, a point B with distance x, the angle of elevation of top of tower is 60°.
When shadow of tower becomes 40 meter more from B than angle of elevation from A becomes 30°.

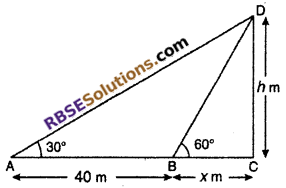
Let BC = x m and ∠CBD = 60°, ∠CAD = 30°
From right angled ∆BCD,
tan 60° = \(\frac { h }{ x }\)
⇒ \(\sqrt { 3 }\) = \(\frac { h }{ x }\)
⇒ x = \(\frac { h }{ \sqrt { 3 } }\)
From right angled ∆ACD

Hence, height of tower is 34.64 m

Question 17.
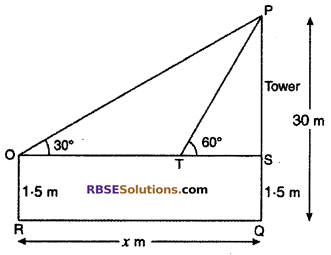
The angle of depression of two ships from the (RBSESolutions.com) top of light house situated at 60 m height from sea-level, are 30° and 45° if two ships are on the same side of the light house, then find the distance between two ships.
Solution :
Let AB is a light house of height 60 m and point C and D are two position of ships.

One ship is exactly behind the other on the same side of the light house. The angle of depression of two ships 30° and 45°.
∠PAC = 300 and ∠PAD = 45°
∠ACD = ∠PAC = 30° (alternate angle)
∠ADB = ∠PAD = 45° (alternate angle)
Let CD = x m
From right angled ∆ABD,
tan 45° = \(\frac { AB }{ BD }\)
1 = \(\frac { 60 }{ BD }\)
⇒ BD = 60 m …..(i)
From right angled ∆ABC,

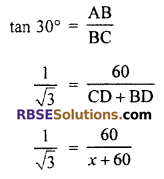
[∵ From equation (i) BD = 60 m]
x + 60 = 60√3
x = 60√3 – 60
= 60(√3 – 1)
= 60 × (1.732 – 1)
= 60 × 0.732
= 43.92 m
Hence, distance between two ships = 43.92 m

Question 18.
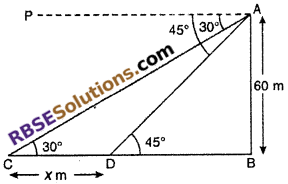
A 1.5 m tall boy is standing at some distance (RBSESolutions.com) away from a 30 m high building when he moves towards the building then angle of elevation from his eye became 60° from 30°. Find how much distance he covered towards the building?
Solution :
Let PQ be the building of height 30 m. A boy is standing at point R with distance x m from the base of building Q with height QR = 1.5 m, then

OS || PQ and QR || SQ
∴ SQ = OR = 1.5 m
∴ PS = PQ = SQ
= 30 – 1.5 = 28.5 m
The angle of elevation from the eyes of the boy to (RBSESolutions.com) the top of building is 30° and as the boy walks towards the building the angle of elevation
becomes 60°.
∠PQS = 30° and ∠PTS = 60°
From tight angled ∆PSO,

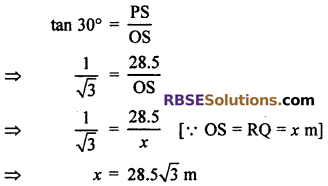
Let a boy walks some distance and reach point T where (RBSESolutions.com) the angle of eyes becomes 60° then from right angled ∆PTS,
tan 60° = \(\frac { PS }{ TS }\)
\(\sqrt { 3 }\) = \(\frac { 28.5 }{ TS }\)
TS = \(\frac { 28.5 }{ \sqrt { 3 } }\)
Distance covered toward the building
OT = OS – TS
= 28.5√3 – \(\frac { 28.5 }{ \sqrt { 3 } }\)

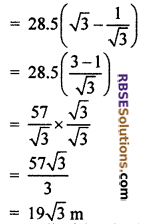
Hence, distance walked by the boy towards the building = 19√3 m

Question 19.
Angle of elevation of top of a tower from a 7 m (RBSESolutions.com) high building is 60° and angle of depression of its foot is 45°. Find the height of the tower.
Solution :
Let AB is a tower and CD is a building of height 7 m.
The angle of elevation and angle of depression are 60° and 45° respectively.
i.e., ∠ACE = 60°
and ∠ECB = 45°
BD || CE, CD || BE
∴ CD = BE = 7 m

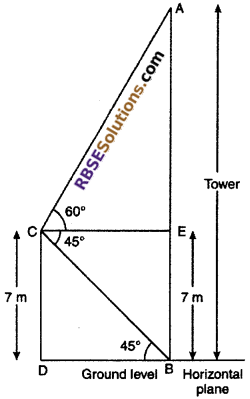
From right angled ∆CBD
tan 45° = \(\frac { CD }{ DB }\)
⇒ 1 = \(\frac { 7 }{ DB }\)
∴ DB = 7 m
CE = DB = 7 m
Again from right angled ∆AEC
tan 60° = \(\frac { AE }{ CE }\)
\(\sqrt { 3 }\) = \(\frac { AE }{ 7 }\)
AE = 7√ m
Hence, height of tower AB = AE + EB
= 7√3 + 7
= 7(√3 + 1) m
Hence, height of tower AB = 7(√3 + 1) m

Question 20.
From the top of a hill, in east side at two (RBSESolutions.com) points angle of depressions are 30° and 45°.
If distance between two points is 1 km, then find height of the hill.
Solution :
Let height of hill AB is h km. In the east side of hill there are two points C and D respectively.
The angle of depression are 30° and 45°. The distance between CD = 1 km.

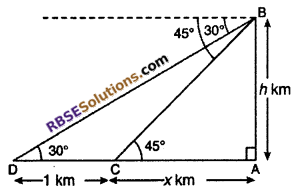
Let AC = x km
From right angled ΔACB
tan 45° = \(\frac { AB }{ AC }\)
⇒ 1 = \(\frac { h }{ x }\)
⇒ h = x
From right angled ΔDAB,
tan 30° = \(\frac { AB }{ AD }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { h }{ x+1 }\)
⇒ √3h = x + 1
Put the value of x from (RBSESolutions.com) equation (i) in equation (ii)
√3h = h + 1
√3h – h = 1
h(√3 – 1) = 1
h = \(\frac { 1 }{ \sqrt { 3 } -1 } \) = \(\frac { 1 }{ 1.732-1 }\) = \(\frac { 1 }{ 0.732 }\)
= 1.366 km
Hence, height of hill = 1.366 km

Question 21.
The angle of elevation of a cloud from a point 20 m above a lake (point A) is 30°. If the angle of depression of its reflection from point A is 60°, then find the distance of cloud from point A.
Solution :
Let BD be the surface of water. A is the point of observation. P be the position of cloud and C be the position of the reflection of cloud in the lake. Draw AQ ⊥ PD. Angle of elevation of cloud (RBSESolutions.com) from point A is 30° i.e., ∠PAQ = 30° and depression of the reflection of cloud in the lake is 60° i.e, ∠QAC = 60°
Let PQ = h m

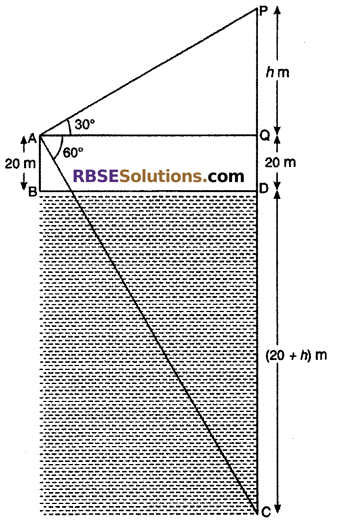
So, ∠PAQ = 30° and ∠QAC = 60°
QD = AB = 20 m
CD = PD = (20 + h)m
QC = 20 + h + 20
= (40 + h) m
BD = AQ
From right angled ∆PAQ,
tan 30° = \(\frac { PD }{ AQ }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { h }{ AQ }\)
⇒ AQ = h√3 m
From right angled ∆AQC,
tan 60° = \(\frac { QC }{ AQ }\)
⇒ \(\sqrt { 3 }\) = \(\frac { 40+h }{ h\sqrt { 3 } } \) [∵ From equation (i), AQ = h√3]
h√3 × √3 = 40 + h
⇒ 3h = 40 + h
⇒ 2h = 40
⇒ h = \(\frac { 40 }{ 2 }\) = 20 m
From right angled ∆PAQ
sin 30° = \(\frac { PQ }{ AP }\)
⇒ \(\frac { 1 }{ 2 }\) = \(\frac { h }{ AP }\)
⇒ \(\frac { 1 }{ 2 }\) = \(\frac { 20 }{ AP }\)
⇒ AP = 20 × 2 = 40 m
Hence, distance of cloud from A = 40 m

Question 22.
From a point on a bridge across a river, the angles (RBSESolutions.com) of depression of the banks on opposite side of the river are 30° and 45°, respectively. If the bridge is at height of 4 m from the bank, find the width of the river.
Solution :
Given : Height of bridge from river
AO = 4 m
BO = x, CO = y

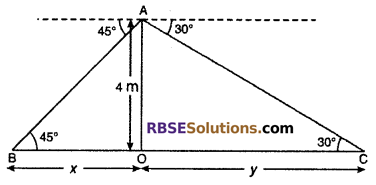
From right angled ∆AOB
\(\frac { AO }{ BO }\) = tan 45°
⇒ \(\frac { 4 }{ x }\) = 1
⇒ x = 4 m ……(i)
Again from right angled ∆AOC,
\(\frac { AO }{ CO }\) = tan 30°
⇒ \(\frac { 4 }{ y }\) = \(\frac { 1 }{ \sqrt { 3 } }\)
⇒ y = 4√3 m ……(ii)
From equation (i) and (ii)
Width of river = x + y
= 4√3 + 4
= 4(√3 + 1)
= 4(1.732 + 1)
= 4(2.732)
= 10.92 m
Hence, width of river is 10.92 m

Question 23.
A man on the deck of the ship is 10 m above (RBSESolutions.com) water-level. He observes that the angle of elevation of the top of hill is 60° and the angle of depression of the base is 30° then find the distance of the hill from the ship and height of the hill.
Solution :
Let AE is a deck of the ship of height 10 m and CD is a hill. From point A, the angle of elevation of the top of hill is 60° and the angle of depression of the base is 30°.
Let BC = h
and ED = x
∠CAB = 60°, ∠BAD = ∠ADE = 30° (Alternate angle)

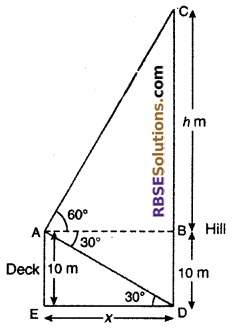
From right angled ΔAED
tan 30° = \(\frac { AE }{ ED }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { 10 }{ x }\)
⇒ x = 10√3 m
From right angled ΔABC
tan 60° = \(\frac { BC }{ AB }\)
⇒ \(\sqrt { 3 }\) = \(\frac { h }{ 10\sqrt { 3 } } \)
⇒ h = 10√3 × √3 = 30 m
Hence, height of hill CD= BD + BC
= 10 + 30 = 40 m
And the distance of the hill from the ship = ED = x = 10√3 m
Hence, distance of the hill from the ship = 10√3 m and height of hill = 40 m.

Question 24.
A vertical straight tree 12 m high is broken (RBSESolutions.com) by strong wind in such a way that its top touches the ground and makes an angle of 60° with the ground. Find at what height from the ground did the tree break? (√3 = 1.732)
Solution :
Let BD is a tree of height 12 m. Suppose it got bent at a point C and let the part CD take the position CA, meeting the ground at A.

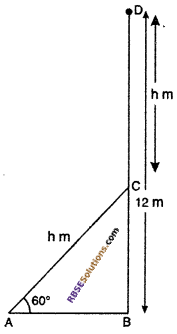
i.e., CD = AC = h m
(let)
Broken part makes 60° angle from ground So, ∠BAC = 60°
Now height of remaining part of tree = (12 – h)m.
From right angled ∆ABC
sin 60° = \(\frac { BC }{ AC }\)
⇒ \(\frac { \sqrt { 3 } }{ 2 } \) = \(\frac { 12-h }{ h }\)
⇒ √3h = 2(12 – h)
⇒ √3h = 24 – 2h
⇒ √3h + 2h = 24
⇒ h(√3 + 2) = 24
⇒ h(1.732 + 2) = 24
⇒ h(3.732) = 24
⇒ h = \(\frac { 24 }{ 3.732 }\) = 6.4308 m
Hence, height of broken tree from ground = BC
= 12 – h
= 12 – 6.4308
= 5.569 m
Hence, tree ¡s broken 5.569 m from ground.

Question 25.
A straight highway leads to the foot of a tower. (RBSESolutions.com) A man standing at the top of the tower observes a car at an angle of depression of 30°, .which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution :
Let BCD is a highway. A tower is standing at point D of height h. From the top of tower of point A the angle of depression is 30°. After 6 sec when car reaches at point C then angle of depression becomes 60°. Hence distance covered in 6 sec = BC

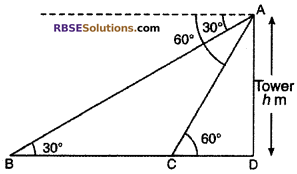
From right angled ∆ADB,
tan 30° = \(\frac { AD }{ BD }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { h }{ BD }\)
⇒ BD = h√3 …..(i)
Again, From right angled ∆ADC,
tan 60° = \(\frac { AD }{ CD }\)
⇒ \(\sqrt { 3 }\) = \(\frac { h }{ CD }\)
⇒ h = √3CD …..(ii)
Put the value of h in equation (i),
BD = √3CD × √3 = 3CD
BC + CD = 3CD
2CD = BC
CD = \(\frac { 1 }{ 2 }\) BC
Since car is moving with uniform speed (RBSESolutions.com) and distance CD is half of BC.
Hence, time taken to cover distance CD
= \(\frac { 1 }{ 2 }\) × time taken to cover distance BC
= \(\frac { 1 }{ 2 }\) × 6
= 3 sec.
Hence, required time = 3.

Question 26.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line are complementary. Prove that the height of tower is 6 m.
Solution :
Let CD is a tower of height h m. A and B are two points (RBSESolutions.com) such that AC = 9 m and BC = 4 m.

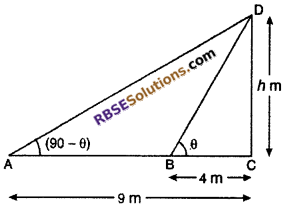
Let ∠DBC = θ
Then its complement will be ∠DAC = (90° – θ)
From right angled ∆DCB,
tan θ = \(\frac { DC }{ BC }\)
tan θ = \(\frac { h }{ 4 }\) …..(i)
From right angled ∆DCA,
tan(90° – θ) = \(\frac { DC }{ AC }\)
cot θ = \(\frac { h }{ 9 }\)
⇒ \(\frac { 1 }{ tan\theta } \) = \(\frac { h }{ 9 }\) …..(i)
multiply equation (i) and (ii),
tan θ × \(\frac { 1 }{ tan\theta } \) = \(\frac { h }{ 9 }\) × \(\frac { h }{ 9 }\)
or 1 = \(\frac { { h }^{ 2 } }{ 36 }\)
⇒ h² = 36
⇒ h = 6 m
Hence, height of tower = 6 m

Question 27.
A tower and a building on the opposite side of road are (RBSESolutions.com) situated. The angles depression from the top of tower at the roof and base of building are 45° and 60° respectively. If height of building Is 12 m then find the height of the tower. (√3 = 1.732)
Solution :
Let AB is a building of height 12 m. CE is a tower. Let ED = h m
The angles of depression from point E of top of tower at the roof and base on building are 45° and 60° respectively. Now
∠XEA = ∠EAD = 45° (Alternate angle)
∠XEB = ∠EBC = 60° (Alternate angle)

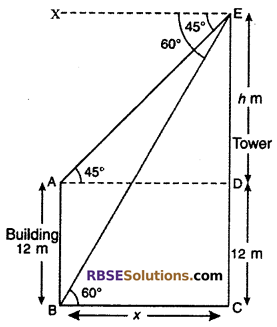
Let BC = x and ED = h m
AB = CD = 12 m
From right angled ΔEAD,
tan 45° = \(\frac { ED }{ AD }\)
l = \(\frac { h }{ x }\)
⇒ h = x …(i)
From right angled ΔEBC,
tan 60° = \(\frac { h+12 }{ BC }\)
√3 = \(\frac { h+12 }{ x }\) = \(\frac { h+12 }{ h }\) (Put the value of x from equation (i))
⇒ √3h = h + 12
⇒ √3h – h = 12
⇒ h[1.732 – 1] = 12
⇒ h = \(\frac { 12 }{ 0.732 }\)
= 16.393 m
Hence, height of tower = EC = CD + ED
= 12 + 16.393
= 28.393 m

Question 28.
If angle of elevation of sun changes (RBSESolutions.com) from 30° to 60°. Then at these angles of elevation find the difference in the length of shadow of 15 m high pillar.
Solution :
Let AD is a pillar of height = 15 m
The angle of elevation from point B of ground is 30° and angle of elevation from point C is 60°.
∠ABD = 30° and ∠ACD = 60°

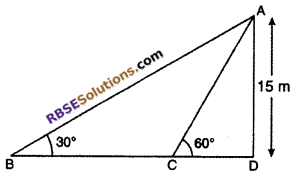
From right angled ∆ADC

From right angled ∆ADB
tan 30° = \(\frac { AD }{ BD }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { 15 }{ BD }\)
⇒ BD = 15√3 m
Difference in length of shadow = BC
= BD – CD
= 15√3 – 5√3
= 10√3 m
= 10 × 1.732
= 17.32 m
Hence, difference in length of (RBSESolutions.com) shadow = 17.32 m

We hope the given RBSE Solutions for Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 8 Height and Distance Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.