RBSE Solutions for Class 11 Chemistry Chapter 5 States of Matter: Gas and Liquid

Rajasthan Board RBSE Class 11 Chemistry Chapter 5 States of Matter: Gas and Liquid

RBSE Class 11 Chemistry Chapter 5 Text Book Questions

RBSE Class 11 Chemistry Chapter 5 Multiple Choice Questions

Question 1.
Unit of R in Ideal gas equation is
(a) mole atm K^-1
(b) lit mole
(c) erg K^-1
(d) lit atm K^-1 mole^-1
Answer:
(d) lit atm K^-1 mole^-1

Question 2.
The temperature and pressure at which water, ice and water vapour exist together is called:
(a) 0°C, 1 atm
(b) 0°C, 4.7 atm
(c) 2° C, 4.7 atm
(d) -2° C , 4.7 atm
Answer:
(b) 0°C, 4.7 atm

Question 3.
Which of the following gas has highest diffusion?
(a) NH₃
(b) N₂
(c) CO₂
Answer:
(a) NH₃

Question 4.
If the volume of two moles of an ideal gas is at 546 K, then its pressure will be :
(a) 2 atm
(b) 1 atm
(c) 4 atm
(d) 3 atm
Answer:
(a) 2 atm

Question 5.
If absolute temperature of an ideal gas is doubled and pressure is halved then volume of gas will be :
(a) Double
(b) Four times
(c) One-fourth
(d) Unchanged
Answer:
(b) Four times

RBSE Class 11 Chemistry Chapter 5 Very Short Answer Type Questions

Question 6.
What is the difference between boiling and evaporation ?
Answer:

• Evaporation occurs at the surface of the liquid whereas boiling occurs at the entire liquid.
• Evaporation occurs at any temperature whereas boiling occurs at a specific temperature.

Question 7.
Why boiling point of liquid increases on increasing the pressure?
Answer:
The boiling point of a liquid is the temperature at which the vapour pressure of the liquid becomes equal to the atmospheric pressure. The vapour pressure of a liquid is also a function of the temperature. As the temperature increases the vapour pressure increases.

Now if we increase the external pressure, a higher temperature would be required so that the vapour pressure becomes equal to the external pressure and hence the boiling point of the liquid increases.

Question 8.
What does the ‘zero’ value of van der Waal’s constant ‘a’ for a gas indicate?
Answer:
The Van der Waal’s equation is

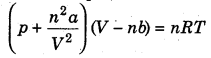
Zero value of ‘a’ indicates least intermolecular force of attraction and no liquifaction

Question 9.
Why Kelvin scale of temperature is better than Celsius scale of temperature?
Answer:
The Kelvin scale is based on absolute zero which means it will never go negative unlike Celsius scale. That is why it is convenient for all scientific calculations.

Question 10.
Why does the vegetable cook with ^difficulty at hill stations?
Answer:
The boiling point of water depends upon the pressure on its surface. It increases with increase of pressure and decreases on lowering of pressure. At higher altitudes, the atmospheric pressure is low and, therefore water boils below 100^oC. Hence, sufficient heat is not supplied for cooking the vegetables at hill stations. This difficulty may be overcome by using a pressure cooker.

Question 11.
Why a gas could not be cooled at absolute temperature?
Answer:
The gas will no longer be a gas at absolute zero, but rather a solid. As the gas is cooled, it will make a phase transition from gas into liquid, and upon further cooling from liquid to solid (ie. freezing)

Question 12.
What is the SI unit of pressure?
Answer:
The SI unit of pressure is the Pascal’s (Pa), which is equal to one Newton per square metre(N/m²)

Question 13.
Compressibility factor Z is less than one for any gas. Why?
Answer:
The deviation from ideal behaviour can be measured in terms of compressibility factor Z, which is the ratio of product PV and nRT.
Mathematically,
Z = PV/nRT
For ideal gas, Z = 1 at all temperatures and pressures because PV = n RT

At intermediate pressure, most gases have z < 1, because gases show ideal behaviour when the volume occupied is large so that the volume of the molecules can be neglected in comparison to the volume of gas. Also, gases have some force of attraction between the molecules.

Question 14.
What is Boyle’s temperature?
Answer:
The temperature at which a real gas obeys ideal gas law over an appreciable range of pressure is called Boyle’s temperature or Boyle’s point. Boyle’s point of a gas depends upon its nature. Above the Boyle’s point, real gases show positive deviations from ideality and Z values are greater than one.

Question 15.
Which of the following has high viscosity-water or glycerine?
Answer:
Viscosity is another type of bulk property defined as a liquid’s resistance to flow. When the intermolecular forces of attraction are strong within a liquid, there is a larger viscosity. Therefore, molecular forces regarding to chemical bonds should to be stronger for glycerine than water. The viscosity of water results from hydrogen bonds between the positively charged hydrogen atoms and the negatively charged oxygen atoms. Glycerine (HOH₂C-CHOH—CH₂OH) contains three hydroxyl groups, which leads to a higher number of hydrogen bonds and therefore stronger bonds between molecules have higher viscosity.

Question 16.
At normal temperature and pressure, what is the molar volume of an ideal gas?
Answer:
At normal temperature and pressure ( NTP ), for Ideal gas
V_molar = 293K × 0.0820 L atm/(mol-K)/1atm × 1 mol
V_molar = 2404 L

Question 17.
If at constant temperature and atmospheric pressure, a gas expands from 20 cm³ to 50 cm³, what will be its final pressure?
Answer:
According to Boyle’s law,
P₁V₁ = P₂V₂
P₁ = 1 atm
P₂ = ?
V₁ = 20 cc
V₂ = 50 cc
P₂ =(P₁ × V₁)/V₂
P₂ = 1 × 20/ 50 = 2/ 5 atm = 0.4 atm

Question 18.
Mixture of NH₃ and HCl gases do not follow Dalton’s law of partial pressure. Why?
Answer:
Mixture of NH₃ and HCl gases do not follow Dalton’s law of partial pressure because the gases are reactive. They react to form ammonium chloride which is solid and Dalton’s law of partial pressure is not applicable to solids and reactive gases.
NH₃ + HCl ➝ NH₄Cl

Question 19.
In which two conditions, ideal gases show deviation?
Answer:
The causes of deviations from ideal behaviour may be due to the following two assumptions of kinetic theory of gases:
The volume occupied by gas molecules is negligibly small as compared to the volume occupied by the gas. The forces of attraction between gas molecules are negligible.
This is valid only at low pressure and high temperature, when the volume occupied by the gas molecules is negligible as compared to the total volume of the gas. Two conditions in which ideal gases show deviation :

1. At low temperature or
2. At high pressure

The volumes of molecules are no more negligible as compared to the total volume of the gas and the gas molecules interact with each other due to proximity.

Question 20.
What will be the volume of 0.5 mole of a gas at 273 K and 1 atm pressure ?
Answer:
At 273 K and 1 atm pressure (STP):
Volume of 1 mole of gas is 22.4 lit (As per Gas Law)
So, volume of 0.5 mole of gas = 22.4/2 = 11.2 lit

RBSE Class 11 Chemistry Chapter 5 Short Answer Type Questions

Question 21.
The drops of liquid take spherical shape. Why?
Answer:
The inward forces on the surface molecules of a liquid drop tend to cause the surface-to-volume ratio as small as possible. Since surface-to-volume ratio is minimum for the spherical shape so a liquid drop is spherical.

Question 22.
What is the effect of heat on surface tension?
Answer:
Liquids tend to minimize their surface area because molecules of the liquid at the Surface experience net attractive force towards the interior of the liquid, this characteristic property of the liquid is known as surface tension. In general, surface tension decreases when temperature increases because cohesive forces decrease with an increase of molecular thermal activity. Increase in temperature increases the kinetic energy of the molecules and effectiveness of intermolecular attraction decreases, so surface tension decreases as the temperature is raised.

Question 23.
The boiling point of liquid changes on increasing the pressure. Why?
Answer:
The boiling point of a liquid is the temperature at which the vapour pressure of the liquid becomes equal to the atmospheric pressure pressure. Also the vapour pressure of a liquid is a function of the temperature. As the temperature increases, the vapour pressure increases. Now if we increase the external pressure, a higher temperature would be required so that the vapour pressure equal to that increased external pressure and hence, the boiling point of the liquid increases.

Question 24.
Why viscosity of ethanol is higher than ethers?
Answer:
Viscosity refers to the resistance to flow in a liquid. The intermolecular attractions between molecules in a liquid affect its viscosity. When the intermolecular forces of attraction are strong within a liquid, there is a larger viscosity. Alcohols have hydrogen bonding which are typically much stronger attractions than ordinary dipole moments. Therefore, its viscosity is high. Also, a group of ethanol molecules is much harder to separate from each other than a group of ether molecules.

Question 25.
What is the physical significance of van der Waal’s constants ‘a’ and ‘b’ ?
Answer:
Van der Waal’s equation :

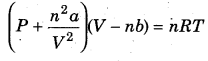
Physical significance of ‘a’ : ‘a’ is a measure of the magnitude of intermolecular attractive forces between the particles.
Physical significance of ‘b’ : The van der Waal’s parameter ‘b’ is a measure of the volume of a gas molecule.

Question 26.
The critical temperatures of CO₂ and CH₄ gases are 31.1°C and -81.9°C. Which of the two has strong intermolecular forces and why ?
Answer:
The maximum temperature at which a gas can be converted into a liquid by an increase in pressure is called its critical temperature (T_C). The liquification of a gas becomes easier with the increase in critical temperature, which means that the intermolecular forces of attraction between the molecules of a gas are directly proportional to its critical temperature. Here, the critical temperature for carbon dioxide is higher. Hence, intermolecular forces of attraction are stronger in the case of carbon dioxide.

Question 27.
What do you understand by critical temperature of gases ?
Answer:
Gases become more difficult to liquify as the temperature increases because the kinetic energies of the particles that make up the gas also increase. The critical temperature of a substance is the temperature at and above which vapour of the substance cannot be liquified, no matter how much pressure is applied. Every substance has a critical temperature. Some examples are given as below:

Question 28.
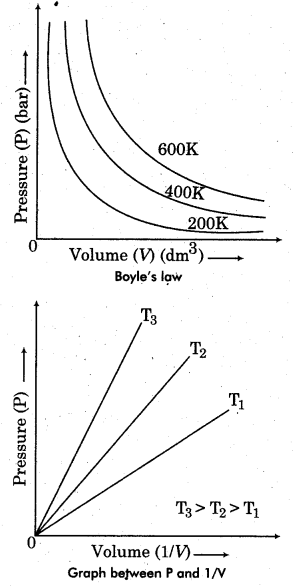
Define Boyle’s Law.
Answer:
According to this law, “At constant temperature, the pressure of a fixed amount (i.e., number of moles n) of gas varies inversely with its volume”. This is known as Boyle’s law. Mathematically, it can be represented as :
P ∝ 1/V (at constant T and n)
Or, PV = k = constant
where, P = Pressure of gas
V = Volume of gas
k = Proportionality constant
The value of constant k depends upon the amount of the gas, temperature of the gas and the units in which P and V are expressed. Thus, the law can also be stated as product of volume and pressure for a given mass of gas at constant temperature is always constant. Graphically this law can be represented as:

Question 29.
Which of the two, ‘Ax’ or ‘Kr’ has higher boiling point and why?
Answer:
Kr has higher boiling point because it has a higher molecular weight (84 amu vs 40 amu). Consider the size pf the atoms and the interatomic forces (since the noble gases exist as single atoms) involved. The only forces are van der Waal’s (or London Dispersion) forces. These are a function of the polarizability of the atom, which is determined by diffusion of the electron cloud. The size of the atoms increases as we go down the group in Periodic table. It also increases as number of electrons increases. Hence, the electron cloud gets bigger, and the polarizability also increases. The electrons can move around easily so there will be instantaneous dipole moments (one side will be + and the other side will be -) which will also result in greater van der Waal’s/London Dispersion forces. Therefore, Kr has higher boiling point than Argon.

Question 30.
Which force is present between molecules of polar molecules like HCl?
Answer:
Dipole-dipole interactions are present in polar molecules like HCl. HCl molecules have a permanent dipole moment because the hydrogen atom has a slight positive charge and the chlorine atom has a slight negative charge. Because of the force of attraction between oppositely charged particles, there is a small dipole-dipole force of attraction between adjacent HCl molecules.

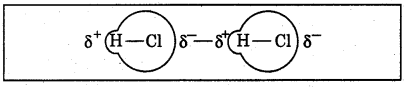
Question 31.
State Ideal gas equation and law.
Answer:
Ideal gas law is a law relating the pressure, temperature and volume of an ideal gas.
Ideal gas equation is combination of three laws (Boyle’s Law, Charles’ Law and Avogadro Law) and gives a single equation (PV = nRT) called as Ideal gas equation.
Mathematically,
According to Boyle’s law; at constant T and n,
V ∝ 1/P …(1)
According to Charle’s law; at constant P and n,
V ∝ T …(2)
According to Avogadro law; at constant T and n,
V ∝ n …(3)
From equation 1, 2 and 3; we get,
V ∝ nT/P …(4)
Or, V = RnT/P …(5)
or, PV = nRT …(6)
Then, R =PV/nT …(7)
Where, R is a gas constant which is same for all gases and known as Universal gas coristant and equation (6), PV = nRT is known as ideal gas equation.

Question 32.
If two moles of an ideal gas at 546 K have volume 44.8 L, then what will be its pressure ?
Answer:
We know that, PV= nRT … (i)
Where, P = Pressure of gas
V = Volume of gas = 44.8L
n = Number of moles of gas = 2
R = Gas constant = 0.082 L atm K^-1 mol^-1
T = Temperature of gas = 546 K
From equation (i) we have,
P = n RT/V
= 2 × 0.082 × 546/44.8
= 1.998 atm.

Question 33.
What is Dalton’s law of partial pressure?
Answer:
The law was formulated by John Dalton in 1801. It states that the total pressure exerted by the mixture of non-reactive gases is equal to the sum of the partial pressures of individual gases i.e., the pressures which these gases would exert if they were enclosed separately in the same volume and under the same conditions of temperature. In a mixture of gases, the pressure exerted by the individual gas is called partial pressure.
Mathematically, P_total = P₁ + P₂ +P₃ (at constant T,V)
Where- P_total is the total pressure exerted by the mixture of gases and P₁, P₂, P₃ etc. are partial pressures of gases.
Or
According to Dalton’s law of partial pressure, “Total exerted pressure by mixture of all non-reactive gases is equal to the sum of partial pressure of all individual gases.”

At constant temperature T and volume V P_total = P₁ + P₂ + P₃
Where, P_total = total exerted pressure of mixture of all gases.
P₁, P₂, P₃ etc. is pressure exerted by individual gases known as partial pressure.

Question 34.
In a gaseous mixture, the ratio of O₂ and N₂ by mass is 1 : 4. What is the ratio of their numbers ?
Answer:
According to the question,
Weight of oxygen = 1
Weight of Nitrogen = 4
Molar mass of O₂ = 32 amu
Molar mass of N₂ = 28 amu
(This means that if you take 32 grams of oxygen or 28 grams of nitrogen, it will contain approximately 6.022 × 10²³ molecules)
Let the mass of oxygen taken be Y grams then according to the question, the mass of nitrogen is 4Y grams. Now to calculate the number of particles, we divide the mass taken by amu.
No. of particles for oxygen we get, Y/32.
No. of particles for nitrogen we get, 4Y/28.
Now the ratio of number of particles for oxygen by nitrogen is
= (Y/32)/(4Y/28)
= Y/32 × 28/4Y
= 7/32 …Required ratio

Question 35.
What is surface tension?
Answer:
Surface tension is defined as the force acting per unit length perpendicular to the line drawn on the surface of liquid. It is denoted by Greek letter γ (Gamma). The energy required to increase the surface area of the liquid by one unit is defined as surface energy. It has dimensions of kg s^-2 and in SI unit it is expressed as N m^-1. The lowest energy state of the liquid will occur when surface area is minimum. Spherical shape satisfies this condition.Thus, liquid drops are spherical in shape at lower energy. It is surface tension which gives stretching property to the surface of a liquid. The magnitude of surface tension of a liquid depends on the attractive forces between the molecules.

RBSE Class 11 Chemistry Chapter 5 Long Answer Type Questions

Question 36.
Write a short note on the following :
(i) Viscosity
(ii) Vapour pressure
(iii) Hydrogen bond.
Answer:
(i) Viscosity : It is a measure of resistance to flow that arise due to internal friction between the layers of liquid (or fluid), when they slip over one another, during the flow of liquid or fluid.
Force required to maintain flow of liquid layers is—
F = ηAdu/dz
Where, A is area of contact,
du/dz is velocity gradient,
η is coefficient of viscosity.

(ii) Vapour pressure—At a particular temperature, pressure exerted by vapour on the walls of the container when water and vapour are in equilibrium, is known as vapour pressure.
H₂O (water) ➝ H₂O (vapour)

Rate of condensation of liquid is directly proportional to concentration of molecules in vapour state. Here, liquid and vapour are in equilibrium. When the temperature of liquid is increased, the number of molecules with higher kinetic energy increases and enter into vapour phase, hence, with increase in temperature, vapour pressure of liquid increases. The temperature at which vapour pressure of liquid oecomes equal to the atmospheric pressure is called boiling temperature at that pressure,

(iii) Hydrogen bond : A hydrogen bond is a type of attractive (dipole-dipole) interaction between an electronegative atom and a hydrogen atom bonded to another electronegative atom. This bond always involves a hydrogen atom. Hydrogen bonds can occur between molecules or within parts of a single molecule. A hydrogen bond tends to be stronger than van der Waal’s forces, but weaker than covalent bonds or ionic bonds. There are two types of hydrogen bonds:
1. Intermolecular hydrogen bond: This type of bond is formed between two or more same or different molecules. Example, water, ammonia etc.
2. Intramolecular hydrogen bond : This type of bond is formed between two different atoms of same molecule. Example : o-nitrophenol.

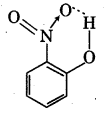
Question 37.
Explain liquification of gases with the help of isotherm of CO₂. Write the process of liquification of gases.
Answer:
Liquification of Gases
Gases can be liquified by increasing pressure and decreasing temperature. On decreasing the temperature, the kinetic energy decreases and intermolecular attraction increases. Gases can be liquified using two methods :

• By cooling.
• By compressing.

Gases with high critical temperature can be liquified by applying appropriate pressure. For example : SO₂ ,NH₃, CO₂, Cl₂ etc.
First of all, Boerhaave in 1732 attempted to liquify gases. He liquified water vapour. Later on in 1799, Van Marum liquified ammonia, in 1800 Mange and Clouet liquified SO₂, in 1805, Narthmore liquified Cl₂, SO₂ and HCl in 1823, Faraday liquified H₂S, CO₂, N₂O, SO₂, NH₃, HBr and other gases.
Cooling of gases can be done using following methods :

• By using a freezing mixture.
• By the evaporation of liquids under reduced pressure.
• By the adiabatic expansion of cold compressed gas.
• Cooling by Joule-Thomson effect.
• Cooling by adiabatic demagnetisation.
• Cooling by desorption.

Andrew’s Experiment and Isotherm of CO₂
Graph plotted between pressure and volume at constant temperature is known as isothermal curve. For ideal gas PV = nRT, if temperature is constant then the PV will be constant. Hence, for ideal gas, isothermal curve will be rectangular hyperbola.

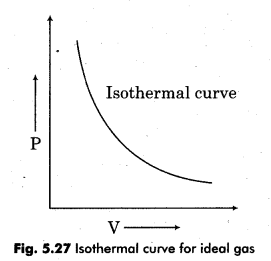
In 1869, Andrews plotted isotherms of CO₂ at various temperatures. It was found that all real gases behave like CO₂. At high temperature, 48°C isotherm of CO₂ looks like that of an ideal gas and gas can not be liquified even at very high pressure. As the temperature is lowered, shape of the curve changes and shows considerable deviation from ideal behaviour. At 30.98°C, carbon dioxide remains as gas upto 73 atmospheric pressure (Point E, in figure 5.28). On increasing the pressure, gas starts to compress and small decrease in volume observed.

At 21.5°C, carbon dioxide remains as gas only upto point B but slowly it becomes liquid i.e., from point B to C.

It is concluded from above explanation that at 31.1°C, CO₂ remains as gas and behave like ideal gas but at 30.98°C (point E) CO₂ appears as liquid for first time. Below this temperature, liquid state is effective. This temperature is known as critical temperature (T_C).

Question 38.
How real gases are different from ideal gases? Derive van der Waal’s equation by pressure and volume modifications.
Answer:
van der Waal’s Equation
On the basis of modification of pressure and volume in kinetic theory of gases, van der Waals corrected ideal gas equation and gave modified form of ideal gas equation. This equation is known as van der Waal’s equation. The corrections made in this equation are following :
1. Correction in Pressure: The real gases deviate from ideal gas behaviour because of interaction of molecules. At high pressure, molecules do not strive the walls of the container with full impact these are dragged back by other molecules due to molecular attractive force. This affects the pressure exerted by the molecules on the walls of the container. Thus the pressure exerted by the gas is lower than the pressure exerted by ideal gas.

Hence,
P = P_i – p
P_i = P + p …(1)
Here p is the pressure correction.
The correction in pressure ‘p’ depends upon following two factors :
1. Number of molecules of gas which exert force on striking molecules.
2. Number of molecules which strike the wall of container per unit area per second.
The decreasing in pressure p is directly proportional to square of density.

2. Volume Correction : van der Waals considered the molecules of real gases as inpentrable spheres having definite volume ‘b’ for ‘n’ number of moles, the restricted volume is ‘nb’. At high pressure, when the molecules are almost in contact, repulsive interactions become significant. Hence, the volume occupied by molecules also became significant because instead of moving in volume V, these are now restricted to volume (V – nb). It can be represented as follows :
Volume of ideal gas (Vi) = Volume of real gas – Volume of molecules of gas
Vi = V – b
Here b is exclude volume of 1 mol of real gas. for n moles Vi=V – nb
Excluded volume (b) is 4 times of volume of molecules of real gas. So for 1 mol of ideal gas,
P_iV_i = RT …(1)
for n moles
P_iV_i = nRT …(2)
where, V_i = ideal volume and P_i = ideal pressure.
Substituting the value of corrected pressure and corrected volume in eq. (2).

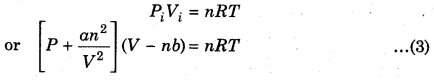
The equation (3) is van der Waal’s equation for n moles of gas, For n = 1 mol, the eq. (3) becomes

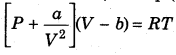
Distinction between Ideal gas and Real Gas
The differences between Ideal gas and Real Gas are given as below:

Question 39.
What is Avogadro’s law? Explain Boyle’s law and Charle’s law with graph.
Answer:
(d) Avogadro’s Law
In 1811, Avogadro established relationship between volume of gas and number of molecules, present in it at given temperature and pressure and which is known as Avogadro’s Law. According to this law, “equal volume of all gases under the same conditions of temperature and pressure contain equal number of molecules”.
Mathematically it is written as :

where V is the volume and n is number of moles of gas. The number of molecules in one mole of a gas has been determined to be 6.023 × 10²³ and is known a Avogadro constant.

Since volume of a gas is directly proportional to the number of moles. Hence, at standard temperature and pressure (STP), one mole of each gas will have same volume. Standard temperature and pressure means 273.15 K and 1 bar (10⁶ pascal).

At STP, molar volume of an ideal gas is 22.4 L mol^-1. Molar volume of some gases is given in table 5.4.
Table 5.4: Molar volume in litres per mole of some gases at 273.15 K and 1 bar (STP).

Boyle’s Law
In 1662, Boyle studied the effect of pressure on given mass of gas at constant temperature. This is known as Boyle’s law or pressure-volume Relation. According to this law “At constant temperature, the pressure of a fixed amount (i.e., number of moles, n) of gas varies inversely with its volume”.
Mathematically, Boyle’s law is written as

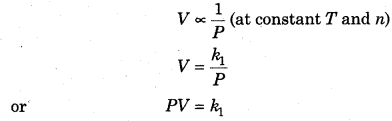
where, P = Pressure, V = Volume, k₁ = proportionality constant.
The value of k₁ depends upon the temperature and mass of gas.
viz “At constant temperature, product of pressure and volume of a fixed amount of gas is constant”.
Suppose, a gas has volume V₁ at pressure P₁. At constant temperature, if pressure extended to P₂ and volume becomes V₂, then according to Boyle’s law,
P₁V₁ = P₂V₂ = Constant

Charle’s Law
The effect of temperature on volume of gas at constant pressure was studied by J. Charle. It was further explained by Gay Lussac and its conclusion was termed as Charle’s Law. Since it gave relation between temperature and volume therefore it is also known as temperature-volume relationship. According to this law, “At constant pressure, the volume of gas increases or decreases by \(\frac{1}{273}\) on increasing or decreasing each degree of temperature”.
Mathematically, Charle’s law can be written as :
Suppose, the volume of gas is V₀ at temperature 0°C. If temperature is increased as t°C then volume becomes V_t, then according to Charle’s law,

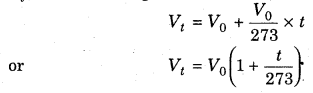
we can calculate the volume of given mass of gas at different temperatures.


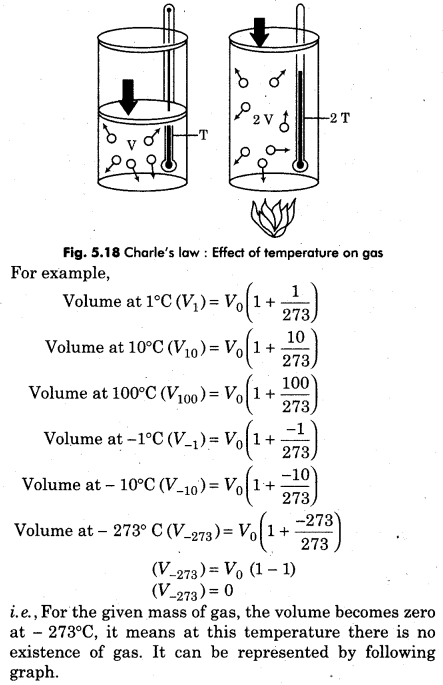
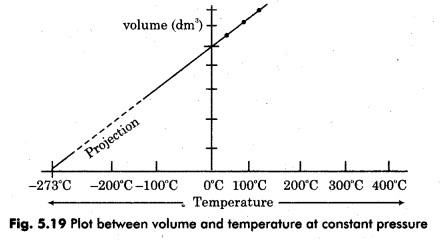
It is clear from graph, at – 273^o or -273.15^oC, the volume of each gas is zero.

RBSE Class 11 Chemistry Chapter 5 Numerical Problems

Question 40.
What will be the minimum pressure required to compress 500 dm³ of air at 1 bar to 200 dm³ at 30°C ?
Solution:
Given that:
Volume of gas (V₁) = 500 dm₃
Pressure of gas (P₁) = 1 bar
Volume of compressed gas (V₂) = 200 dm₃
Now,
Let P₂ be the pressure required to compress the gas.
Therefore at constant temperature, according to Boyle’s law,
P₁V₁ =P₂V₂
or, P₂ = WV₂
= 1 × 500/200 = 2.5 bar
Therefore, the minimum pressure required is 2.5 bar.

Question 41.
At 0°C, the density of a certain oxide of a gas at 2 bar is same as that of dinitrogen at 5 bar. What is the molecular mass of the oxide?
Solution:
We know that relationship of density (d) of the substance at temperature (T) is given as
d = MP/RT
or, P = d RT/ M
According to the question, if M is the molar mass of the gaseous oxide, then
2 = dRT/M …(1)
Also for nitrogen, 5 = dRT/28 …(2) (Given)
Dividing equation (2) by (1), we get
5/2 = M/28
M = 5 × 28/2 = 70 g/mol
Hence, the molecular mass of the oxide is 70 g/mol.

Question 42.
Pressure of 1 g of an ideal gas A at 27°C is found to be 2 bar. When 2 g of another ideal gas B is introduced in the same flask at same temperature, the pressure becomes 3 bar. Find a relationship between their molecular masses.’
Solution:
Given that
Mass of gas A, W_A = 1 g
Mass of gas B, W_B = 2 g
Pressure exerted by the gas A = 2 bar
Total pressure due to both the gases = 3 bar
As temperature and volume remain constant.
Now if M_A and M_B are molar masses of the gases A and B respectively, therefore
P_AV = W_ART/M_A
or, 2 × V = 1 × RT/MA ….. (i)
Also,
P_totalV = (W_A / M_A + W_B / M_B)RT
3 × V = (1/ (M_A + W_B/M_B)RT …….. (ii)
Dividing equation (ii) by (i), we get

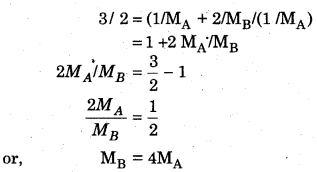
Thus, a relationship between the molecular masses of A and B is given by 4M_A = M_B.

Question 43.
The drain cleaner, Dratnex contains small bits of alluminium which reacts with caustic soda to produce dihydrogen. What volume of dihydrogen at 20 °C and one bar will be released when 0.15 g of aluminum reacts?
Solution:
The reaction of aluminum with caustic soda can be represented as :

Therefore, 201 ml of dihydrogen will be released.

Question 44.
What will be the pressure exerted by a mixture of 3.2 g of methane and 4.4 g of carbon dioxide contained in a 9 dm3 flask at 27°C?
Solution:
Given that,
Mass of carbon dioxide = 4.4 g
Molar mass of carbon dioxide = 44 g/mol
Mass of methane = 3.2 g
Molar mass of methane = 16 g/mol
Now
Number of mole of methane, n_CH4 = 3.2/16 = 0.2 mol and number of mole of CO₂ nCO₂ = 4.4/44 = 0.1 mol Since,
PV = (n_CH4 + n_CO2) RT
Or, P × 9 = (0.2 + 0.1) × 0.0821 × 300
Or P = 0.3 × 0.0821 × 300/ 9 = 0.82 atm
Hence, the total pressure exerted by the mixture is 0.82 atm.

Question 45.
What will be the pressure of the gaseous mixture when 0.5 L of H2 at 0.8 bar and 2.0 L of dioxygen at 0.7 bar are introduced in 1 L vessel at 27°C?
Solution:
The equation PV= nRT for the two gases can be given as :
For H₂
0. 8 × 0.5 = nH₂ × RT or nH₂ = 0.8 × 0.5/RT = 0.4/RT
And, for O₂
0. 7 × 2.0 = n_O2. RT or n_O2 = 0.7 × 2/RT = 1.4/RT When introduced in 1 L vessel, then
P × 1 = (n_O2 + n_H2) RT
Putting the values, we get
P = 0.4 + 1.4 = 1.8 bar
Hence, the total pressure of the gaseous mixture in the vessel is 1.8 bar.

Question 46.
Density of a gas is found to be 5.46 g/dm³ at 27 °C at 2 bar pressure. What will be its density at STP?
Solution:
We know that, for an ideal gas
Density d = P × M/ RT
According to the question,
5.46 = 2 × M/ R × 300 ….. (1)
and, At STP, d = 1 × M/R × 273 …(2)
Dividing equation (ii) by (i)
d/5.46 = (1 × M/273 × R) × (300 × R/2 × M)
d = 300 × 5.46/ 273 × 2 = 3.00 g/dm³
Hence, the density of the gas at STP will be 3 g dm^-3.

Question 47.
4.05 ml of phosphorus vapour weighs 0.0625g at 546 °C and 0.1 bar pressure. What is the molar mass of phosphorus?
Solution:
Given, P = 0.1 bar
V = 34.05 mL = 34.05 × 10^-3L
= 34.05 × 10^-3 dm³
R = 0.083 bar dm³K^-1mol^-1
T = 546°C = (546 + 273) K = 819 K
The number of moles (n) can be calculated using the ideal gas equation as:
From the gas equation
PV = w ,RT/M,we get
M = w. RT/ PV …(1)
Substituting the given values in the equation (1), we get M = (0.0625 / 0.1 × 34.04) × 82.1 × 819 = 124.75 g/mol
Hence, the molar mass of phosphorus is 124.75 g mol^-1 .

Question 48.
Calculate the volume occupied by 8.8 g of CO₂ at 31.1 °C and 1 bar pressure. R = 0.083 bar L K_-1 mol_-1.
Solution:
From the gas equation,
PV = (w/M)RT
Where w = mass of the gas. M = molar mass of the gas. For CO₂, M = 44 g/mol Substituting the given values ,we get
l × V = (R8/44) × 0.083 × 304.1
= 5.05 L
Hence, the volume occupied is 5.05 L.

Question 49.
2.9 g of a gas at 95° C occupied the same volume as 0.184 g of dihydrogen at 17 °C, at the same pressure. What is the molar mass of the gas?
Solution:
From the gas equation,
PV =(w /M)RT
where w = weight of gas .
T₁ = 273 + 95 = 368 K
and T₂ = 273 + 17 = 290 K
Substituting the given data in the gas equation, we get
PV = (2.9/M) × R × 368 ….. (i)
PV = (0.184/2) × R × 290 ….. (ii)
From these two equations, we can write
(2.9/M) × R × 368 = (0.184/2) × R × 290
By striking through R from both sides we get
(2.9/M) × 368 = (0.184/2) × 290
Or (2.9/M) = (0.092 × 290) / 368
Or M = 2.9 × 368/0.092 × 290
= 40 g/mol
Hence, the molar mass of the gas is 40 g mol^-1

RBSE Solutions for Class 11 Chemistry