Rajasthan Board RBSE Class 12 Maths Chapter 15 रैरिवक प्रोग्रामन Ex 15.2
प्रश्न 1.
एक आहार विज्ञानी दो प्रकार के भोज्यों को इस प्रकार मिलाना चाहती है कि प्राप्त मिश्रण में विटामिन A की कम से कम 8 इकाई तथा विटामिन C की कम से कम 10 इकाई विद्यमान हो। भोज्य I में विटामिन A2 इकाई प्रति किलोग्राम तथा विटामिन C1 इकाई प्रति किलोग्राम तथा भोज्य II में विटामिन A, 1 इकाई प्रति किलोग्राम तथा विटामिन C2 इकाई प्रति किलोग्राम विद्यमान है। भोज्य I व II को प्रति किलोग्राम खरीदने की लागत क्रमशः Rs 5 ध Rs 7 है। इस प्रकार के मिश्रण की निम्नतम लागत ज्ञात कीजिये। समस्या का गणितीय सूत्रीकरण करते हुए हल कीजिए।
हल :
माना भोज्य I की x किग्रा तथा भोग्य II की y किग्रा. की मात्रा मिश्रण में है।
∴प्रश्नानुसार 5 प्रति किग्रा को दर से x किग्रा का मूल्य
= Rs 5x
तथा Rs 7 प्रति किग्रा की दर से y किग्रा का मूल्य
= Rs 7y
∴मिश्रण का कुल लागत न्यूनतम मूलय = 5x + 7y
अत: न्यूनतम मूल्य उद्देश्य फलन z = 5x + 7y
मिश्रण में भोज्य I के x किग्रा मात्रा में विटामिन A की कुल इकाई
= 2x
तथा मिश्रण में भोज्य II के y किग्रा मात्रा में विटामिन A की कुल इकाई = y
∴प्रश्नानुसार व्यवरोध 2x + y ≥ 8 ….(1)
इस प्रकार मिश्रण में भोज्य I के x किग्रा. मात्रा में विटामिन C की कुल इकाई = x
तथा मिश्रण में भोज्य II के y किग्रा मात्रा में विटामिन C की कुल इकाई = 2y
∴ प्रश्नानुसार व्यवरोध x + 2y = 10 …(2)
तथा
x ≥ 0, y ≥ 0
अतः समस्या का गणितीय सूत्रीकरण
न्यूनतम लागत मूल्य फलन
z = 5x + 7y
2x + y ≥ 8
x + 2y ≥ 10
x ≥ 0, y ≥ 0
व्यवरोध के रूप में प्राप्त असमिकाओं को समीकरण के रूप में व्यक्त करने पर
2x + y = 8 …(1)
x + 2 = 10 …(2)
असभिका 2x + y ≥ 8 द्वारा प्रदर्शित क्षेत्र –
रेखा 2 + y = 8 निर्देशी अक्षों को क्रमशः बिंदु A(4, 0) तथा B(0, 8) पर मिलती है।
2x + y = 8 के मानों के लिए सारणी
| x | 4 | 0 |
| y | 0 | 8 |
A(4, 0); B(0, 8)
बिंदु A(4, 0) तथा B(0, 8) को अंकित कर रेखा का आलेख खींचते है।
असमिका में मूल बिंदु को प्रतिस्थापित करने पर 2(0) + 0 = 0 ≥ 8 असभिका सन्तुष्ट नहीं होती है।
अत: समस्या का सुसंगत हुल क्षेत्र मूल बिंदु के विपरीत और होगा।
असमिका x + 2y ≥ 10 द्वारा प्रदर्शित क्षेत्र –
रेखा x + 2y = 10 निर्देशी अक्षों को क्रमशः बिंदु C(10, 0) तथा D(0, 5) पर मिलती है।
x + 2y = 10 के मानों के लिए सारणी
| x | 10 | 0 |
| y | 0 | 5 |
C(10, 0); D(0, 5)
बिंदु C(10, 0) तथा D(0, 5) को अंकित कर रेखा का आलेख खींचते हैं।
असमिका में मूल बिंदु को प्रतिस्थापित करने पर 0 + 2(0) = 0 ≥ 10 असमिका सन्तुष्ट नहीं होती है। अत: समस्या का हल क्षेत्र मूल बिंदु से विपरीत और होगा।
x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र –
चूँकि प्रथम पाद का प्रत्येक बिंदु इन दोनों असमिकाओं को सन्तुष्ट करता है। अतः असमिका द्वारा प्रदर्शित क्षेत्र प्रथम पाद होगा।
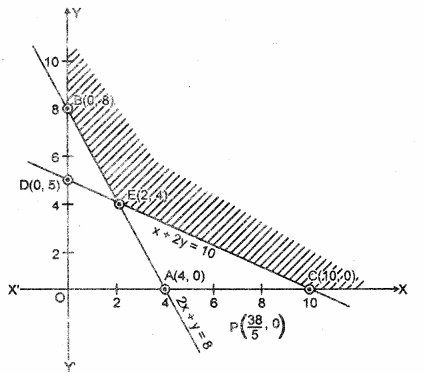
रेखा 2x + y = 8 तथा x + 2y = 10 के प्रतिच्छेद बिंदू E के निर्देशांक x = 2 था y = 4
छायांकित भाग CEB उपर्युक्त असमिकाओं द्वारा उभयनिष्ठ क्षेत्र प्रदर्शित करता है। यह सुसंगत क्षेत्र अपरिबद्ध है। यह क्षेत्र दी गई रैखिक प्रोग्रामन समस्या का सुसंगत हल क्षेत्र है। जिसके कोनीय बिंदु C(10, 0), E(2, 4), B(0, 8) हैं। इन बिंदुओं पर उद्देश्य फलन का मान नीचे सारणी में दिये गये हैं।
| बिन्द | x निर्देशांक | y निर्देशांक | उददेश्य फलन Z = 5x + 7y |
| C | 10 | 0 | ZC = 5 x 10 + 7 x 0 = 50 |
| E | 2 | 4 | ZE = 5 x 2 + 7 x 4 = 38 |
| B | 0 | 8 | ZB = 5 x 0 + 7 x 8 = 56 |
सारणी में बिंदु E(2, 4) पर उद्देश्य फलन का मान निम्नतम Rs 38 है। चूंकि सुसंगत क्षेत्र अपरिबद्ध है। अत: असमिका 5x + 7y ≤ 38 द्वारा निर्धारित परिणामी तुला अद्भुतल, सुसंगत क्षेत्र के माध्य कोई उभयनिष्ठ बिंदु नहीं रखता है।
अत: उद्देश्य फला निन्नतम Z = 3x + 7
व्यवरोध 2x + y ≥ 8
x + 2y ≥ 10
तथा x ≥ 0, y ≥ 0
मिश्रण में भोज्य I की 2 किग्रा तथा II की 4 किग्रा मात्रा मिलाने पर कुल न्यूनतम मूल्य Rs 38 है।
प्रश्न 2.
एक गृहिणी दो प्रकार के भोज्यों X तथा Y को एक साथ इस प्रकार मिलाना चाहती है कि मिश्रण में विटामिन A, B तथा C की क्रमशः कम से कम 10, 12 तथा 8 इकाइयाँ विद्यमान हो। एक किलोग्राम भोज्य में विटामिन संयोजन निम्न प्रकार है
| विटामिन A | विटामिन B | विटामिन C | |
| भोज्य x | 1 | 2 | 3 |
| भोज्य y | 2 | 2 | 1 |
भोज्य X तथा Y के एक किलोग्राम की कीपत क्रमशः Rs 6 व Rs 10 है। इस प्रकार के भोज्य मिश्रण की न्यूनतम कीमत ज्ञात कीजिये।
हल :
माना गृहिणी ने मिश्रण में x किग्रा भोज्य X तथा y किग्रा ज्य Y की मात्रा मिलाई ।
अत: प्रश्नानुसार मिश्रा भोज्य में कुल न्यूनतम कीमत का उद्देश्य फलन
z = 6x + 10y …(1)
व्यवरो के लिये –
विटामिन A के लिये मिश्रण में भोज्य X की x इकाई तथा भोज्य Y की 2y इकाई ली गई हैं।
अत: प्रश्नानुसार x + 2y ≥ 10 ….(1)
विटामिन B के लिये मिश्रण में भोज्य X की 2x इकाई तथा भोज्य Y की 2y इकाई ली गई है।
अत: प्रश्नानुसार 2x + 2y ≥ 12 ….(1)
विटामिन B के लिये मिश्रण में भोज्य X की 2 इकाई तथा भोज्य Y की 2y इकाई ली गई हैं।
अत: प्रश्नानुसार 2x +2y ≥ 12 …(2)
विटामिन C के लिये मिश्रण में भोज्य X की 3x इकाई तथा भोज्य Y की y इकाई ली गई हैं।
अत: प्रश्नानुसार, 3x + y ≥ 8 …(3)
तथा x ≥ 0, y ≥ 0
अतः समस्या के रैखिक प्रोग्रामन का गणितीय सूत्रीकरण निम्न
निम्नतम Z = 6x + 10y
व्यवरोध x + 2y ≥ 10
2x + 2y ≥ 12
3x + y ≥ 8
x ≥ 0, y ≥ 0
ध्यवरोधों के रूप में दी गई असमिकाओं को समीकरण में परिवर्तित करने पर
x + 2y = 10
2x + 2y = 12 …(2)
3x + y = 8 …(3)
असमिका x + 2 ≥ 10 द्वारा प्रदर्शित क्षेत्र –
रेखा x + 2y = 10 निर्देशी अक्षों के क्रमशः बिंदु A(10, 0) तथा B(0, 5) पर मिलती है।
x + 2y = 10 के मानों के लिए सारणी
| x | 10 | 0 |
| y | 0 | 5 |
A(10, 0); B(0, 5)
बिंदुओं A तथा B को अंकित कर रेखा का आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 0 + 2(0) = 0 ≥ 10 असमिका सन्तुष्ट नहीं होती है। अतः असमिका का हल क्षेत्र मूल बिंदु के विपरीत और होगा।
असमिका 2x + 2y ≥ 12 द्वारा प्रदर्शित क्षेत्र –
रेखा 2x + 2y ≥ 12 निर्देशी अक्षों के बिंदु C(6, 0) तथा D(0, 6) पर मिलती है।
2x + 2y = 12
| x | 6 | 0 |
| y | 0 | 6 |
C(6, 0); D(0, 6)
बिंदुओं C और D को अंकित कर रेखा का आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 2(0) + 2(0) = 0 ≥ 12 असमिका सन्तुष्ट नहीं होती है। अतः असमिका का हल क्षेत्र मूल बिंदु के विपरीत और होगा।
असमिका 3x + y ≥ 8 द्वारा प्रदर्शित क्षेत्र –
रेखा 3x + y = 8
निर्देशी अक्षों के बिंदु E(\(\frac { 8 }{ 3 }\), 0) तथा F(0, 8) पर मिलती है।
3x + y = 8 के मानों के लिए सारी
| x | 8/3 | 0 |
| y | 0 | 8 |
बिंदुओं E तथा F को अंकित कर रेखा का आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) प्रतिस्थापित करने पर 3(0) + 0 = 0 ≥ 8 असमिका को सन्तुष्ट नहीं करते हैं। अतः असमिका का हल क्षेत्र मूल बिंदु के विपरीत ओर होगा।
x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र –
चूँकि प्रथम पाद में प्रत्येक बिंदु इन दोनों असमिकाओं को सन्तुष्ट करता है। अतः असमिका का हुल क्षेत्र प्रथम पाई में होगा।
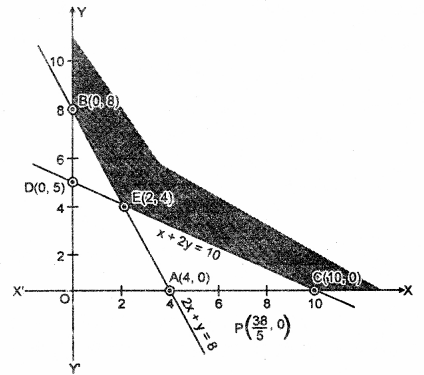
रेखा x + 2y = 10 तथा 2x + 2y = 12 के प्रतिच्छेद बिंदु P(2, 4) के निर्देशांक x = 2 तथा y = 4 हैं।
तथा रेखा 2x + 2y = 12 तथा 3x + y = 8 के प्रतिच्छेद बिंदु Q के निर्देशक Q(1, 5) में x = 1 तथा y = 5 है।
छायांकित क्षेत्र APQF उपरोवत असमिकाओं का हल क्षेत्र है। यह सुसंगत क्षेत्र अपरिबद्ध है। अतः अपरिवद्ध सुसंगत क्षेत्र के कोणीय बिंदुओं के निर्देशांक A( 10, 3), P(2, 4), Q(1, 5) तथा F(0, 8) है। बिंदु P(2, 4), x + 2y = 10 तथा 2x + 2 = 12 रेखाओं का प्रतिच्छेद बिन्दु है त रेखा 2x + 2y = 12 और रेखा 3x + y = 8 के प्रतिच्छेद बिंदु के निर्देशांक Q(1, 5) है।
इन बिंदुओं पर उद्देश्य फलन के मान निम्न तालिका में दिये गये है।
| बिन्द | x निर्देशांक | y निर्देशांक | उदेश्य फ्लन Z=6x+10y |
| A | 10 | 0 | ZA = 6×10+10×0 = 60 |
| P | 2 | 4 | ZP = 6×2+10×4 = 52 |
| Q | 1 | 5 | ZQ = 6×1+10×5 = 56 |
| F | 0 | 8 | ZF = 6×0+10×8 = 80 |
सारणी से स्पष्ट है कि उद्देश्य फलन का मान बिंदु P(2, 4) पर न्यूनतम 52 है।
इसलिये गृहिणी के लिये भोज्य X की 2 किलोग्राम तथा भोज्य Y की 4 किग्रा से मिश्रण बनाने की नीति इष्टतम नीति होगी जिसकी न्यूनतम लागत Rs 52 होगी।
प्रश्न 3.
एक प्रकार के केक को बनाने के लिए 300 ग्राम आटा तथा 15 ग्राम धसा की आवश्यकता होती है, जबकि दूसरे प्रकार के केक को बनाने के लिए 150 ग्राम आटा तथा 30 ग्राम वसा की आवश्यकता होती है। यह मानते हुए कि केकों को बनाने के लिये अन्य सामग्री की कमी नहीं है, 7.5 किलोग्राम आटे तथा 600 ग्राम वसा से। अनाये जा सकने वाले केकों की अधिकतम संख्या ज्ञात कीजिए। समस्या का गणितीय सूत्रीकरण करते हुए आलेखीय विधि से हल कीजिये।
हल :
माना एक प्रकार के केक तथा दूसरे प्रकार के y केक तैयार होते हैं। अत: केक की अधिकतम सीमा का उद्देश्य फलन
Z = x + y
व्यवरोध के रूप में पहले प्रकार के केक में आटा 300x ग्राम तथा दूसरे प्रकार के केक में आटा 150y ग्राम ।
अत: प्रश्नानुसार 300x + 150y ≤ 7500 ग्राम
दूसरे व्यवरोध के रूप में पहले प्रकार के केक में वसा 15x ग्राम तथा दूसरे प्रकार के केक में वसा 30y ग्राम
अत: प्रश्नानुसार, 15x + 30 ≤ 600 ग्राम
दी गई केकों की संख्या कभी ऋणात्मक नहीं हो सकती।
अतः x ≥ 0 तथा y ≥ 0
इसलिये दी गई रैखिक प्रोगामन समस्या का गणितीय सूत्रीकरण निम्न है
अधिकतम Z = x + y
व्यवरोध 300x + 150y ≤ 7500
15x + 30y ≤ 600
x ≥ 0, y ≥ 0
व्यवरोध के रूप में दी गई असमिकाओं को समीकरण में बदलने पर
300x + 150y ≤ 7500
2x + y ≤ 50 ….(1)
तथा 15x + 30y ≤ 600
x + 2y ≤ 40 …(2)
असमिका 2x + y ≤ 50 द्वारा प्रदर्शित क्षेत्र –
रेखा 2x + y = 50 निर्देशी अक्षों को क्रमशः बिंदु A(25, 0) तथा B(0, 50) पर मिलती है।
2x + y = 50 के मानों के लिए सारणी
| x | 25 | 0 |
| y | 0 | 50 |
A(25, 0); B(0, 50) बिंदुओं A तथा B को अंकित कर रेखा का आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 2(0) + 0 = 0 < 50 असमिका को सन्तुष्ट करता है। अतः इस असमिका का हल क्षेत्र मूल बिंदु की ओर होगा।
असमिका x + 2y ≤ 40 द्वारा प्रदर्शित क्षेत्र
रेखा x + 2y = 40 निर्देशी अक्षों को क्रमशः बिंदु C(40, 0) तथा (0, 20) पर मिलती है।
x + 2y = 40 के मानों के लिए सारणी
| x | 40 | 0 |
| y | 0 | 20 |
C(40, 0); D(0, 20) बिंदुओं C और D को अंकित कर रेखा का आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 0 + 2(0) = 0 ≤ 40 असमिका को सन्तुष्ट करता है। अतः असमिका को हल क्षेत्र मूल बिंदु की ओर होगा।
x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र –
चूँकि प्रथम पाद का प्रत्येक बिंदु इन दोनों असमिकाओं को सन्तुष्ट करता है। अतः असमिकाओं x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र प्रथम पाद है।
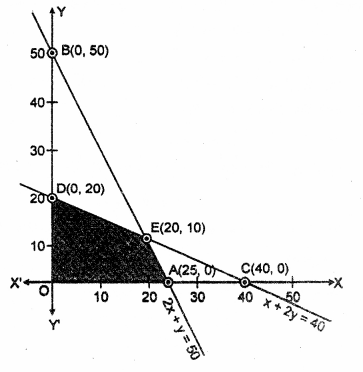
रेखा x + 2y = 40 तथा 2x + y = 50 का प्रतिच्छेद बिंदु E के निर्देशांक x = 20 तथा y = 10.
छायांकित क्षेत्र OAED दी गई असमिकाओं का उभयनिष्ठ क्षेत्र प्रदर्शित करता है। यह क्षेत्र दो गई रैखिक प्रोग्रामन समस्या का सुसंगत हल क्षेत्र है। इस हल क्षेत्र के कोनीय बिंदुओं के निर्देशांक O(0, 0), A(25, 0), E(20, 10) तथा D(0, 20) है।।
इन बिंदुओं पर उद्देश्य फलन के मान नीचे सारणी में दिये गये है
| बिन्द | x निर्देशांक | y निर्देशांक | उदेश्य फ्लन Z=x+y |
| O | 0 | 0 | ZO = 0+0 = 0 |
| A | 25 | 0 | ZA = 25+0 = 25 |
| E | 20 | 10 | ZE = 20+10 = 30 |
| D | 0 | 20 | ZD = 0+20 = 20 |
सारणो से स्पष्ट है कि उद्देश्य फलन का मान बिंदु E(20, 10) पर अधिकतम 30 है। अत: पहले प्रकार के केकों की संख्या 20 तथा दूसरे प्रकार के केकों की संख्या 10 है।
प्रश्न 4.
एक निर्माता औद्योगिक यंत्रों के लिए नट और बोल्ट का उत्पादन करता है। एक पैकेट नटों के उत्पादन के लिए मंत्र A पर 1 एटा तथा यंत्र B पर 3 घण्टे काम करना पड़ता है जबकि एक पैकेट बोल्टों के उत्पादन के लिए यंत्र B पर 3 घण्टे तथा यंत्र B पर 1 घण्टा काम करना पड़ता है। निर्माता नटों तथा खोल्टों के प्रति पैकेट पर लाभ क्रमशः Rs 2.50 तथा Rs 1 कमाता है। यदि वह प्रतिदिन अपने चंत्रों को अधिकतम 12 घण्टे संचालित करता हो तो प्रत्येक (नट और बोल्ट) के कितने पैकेट उत्पादित किए जाने चाहिए ताकि वह अधिकतम लाभ अर्जित कर सके। समस्या का गणितीय सूत्रीकरण कर हल वीजिये।
हल :
माना अधिकतम लाभ अर्जित करने के लिये x पैकेट नट तथा y पैकेट बोल्ट बनाने चाहिये। 1 निर्माता न पर लाभ Rs 2:50 तथा बोल्ट पर Rs 1 प्रति पैकेट कमाता है।
अतः उद्देश्य कथन Z = 2.50x + y अधिकतम मशीन A पर नट बनाने के लिये x घंटे तथा B पर नट बनाने के लिये 3y घंटे काम करना पड़ता है।
अतः व्यवरोध x + 3y ≤ 12 …..(1)
तथा बोल्ट बनाने के लिये मशीन A को 3x घंटे तथा मशीन B को y घंटे काम करना पड़ता है। अतः
व्यरोध 3x + y ≤ 12 ……(2)
चूंकि नट और बोल्ट की संख्या ऋणात्मक नहीं हो सकती है।
∴x ≥ 0 तथा y ≥ 0
दी गई रैखिक प्रोग्रामन समस्या का गणितीय सूत्रीकरण निम्न है
अधिकतम Z = 2.50x + y
यवरोध x + 3y ≤ 12
3x + y ≤ 12
x ≥ 0, y ≥ 0
व्यवरोधों के रूप में दी गई असमिकाओं को समीकरण में व्यस्त करने पर
x + 3y = 12 ….(1)
3x + y = 12 ….(2)
असमिका x + 3y ≤ 12 द्वारा प्रदर्शित क्षेत्र – रेखा x + 3y = 12 निर्देशी अक्षों को क्रमशः बिंदु A(12, 0) तथा B(0, 4) पर मिलती है।
x + 3y = 12 के मानों के लिए सारणी
| x | 12 | 0 |
| y | 0 | 4 |
A(12, 0); B(0, 4)
बिंदु A और B को अंकित कर रेखा का आलेख चते है। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 0 + 3(0) = 0 ≤ 12 असमिका सन्तुष्ट होती है। अतः इस अभिका को हल क्षेत्र मूल बिंदु की और होगा।
असमिका 3x + y ≤ 12 द्वारा प्रदर्शित क्षेत्र – रेखा 3x + y = 12 निर्देशी अक्षों को क्रमश: बिंदु C(4, 2) तथा D(0, 12) पर मिलती है।
3x + y = 12 के मान के लिए करारी
| x | 4 | 0 |
| y | 0 | 12 |
C(4, 0); D(0, 12)
बिंदु C और D को अंकित कर देगा का आलेख चते हैं। असमिका में मूल बिंदु को प्रतिस्थापित करने पर 3(0) + 0 = 0 ≤ 12 असमिका सन्तुष्ट होती है। अतः असमिका का हल क्षेत्र मूल बिंदु की ओर होगः
x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र – चूँकि प्रथम पाद का प्रत्येक बिंदु इन असमिकाओं को सन्तुष्ट करता है। अत: असमिकाओं x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र प्रथम शद होगा।
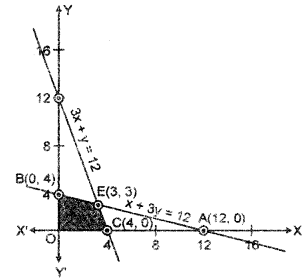
रेखाओं x + 3y = 12 तथा 3x + y = 32 के प्रतिच्छेद बिंदु के निर्देशांक E(3, 3) हैं।
छायांकित क्षेत्र OCEB उपरोक्त असमिकाओं का उभयनिष्ठ क्षेत्र प्रदर्शित करता है। यह क्षेत्र दी गई कि प्रोग्राभन समस्या का सुसंगत
हल क्षेत्र है। इस हल क्षेत्र के कोनीय बिंदु O(0, 0), C(4, 0), E(3, 3) तथा B(0, 4) हैं। इन बिंदुओं पर उद्देश्य फलन का मान निम्न तालिका में दिया गया है।
| बिन्द | x निर्देशांक | y निर्देशांक | उदेश्य फ्लन Z=2.50x+y |
| O | 0 | 0 | ZO = 2.50(0)+0 = 0 |
| C | 4 | 0 | ZC = 2.50(4)+0 = 10 |
| E | 3 | 3 | ZE = 2.50(3)+3 = 10.50 |
| B | 0 | 4 | ZB = 2.50(0)+4 = 4 |
सारणी से स्पष्ट है कि उद्देश्य फलन का मान Z = 10.50 बिंदु E(3, 3) पर अधिकतम है। अत: निर्माता को अधिकतम लाभ प्राप्त करने के लिये नट तथा बोल्ट प्रत्येक के 3 – 3 पैकेट प्रतिदिन बनाने चाहिये।
प्रश्न 5.
एक व्यापारी पंखे तथा सिलाई मशीनें खरीदना चाहता है। उसके पास निवेश करने के लिए केवल Rs 5760 है तथा अधिकतम 20 वस्तुओं को रखने के लिए ही स्थान उपलब्ध है। एक पंखे तथा सिलाई मशीन की कीमत क्रमशः Rs 360 वर Rs 240 है। वह एक पंखे तथा एक सिलाई मशीन को बेचने पर क्रमशः Rs 22 व Rs 18 लाभ कमाता है। यह मानते हुए कि व्यापारी कितनी वस्तुएँ खरीदता है, वे सभी वस्तुएँ वह बेच सकता है। अधिकतम लाभ अर्जित करने के लिए उसे कितने पंखे तथा सिलाई मशीने खरीदनी चाहिए। समस्या का गणितीय सूत्रीकरण कर हल कीजिए।
हल :
माना व्यापारी x पंखे तथा y सिलाई मशीन खरीदता है। अत:
x पंखों की कीमत = Rs 360x
तथा सिलाई मशीनों की कीमत = Rs 240y
अत: प्रश्नानुसार,
360x + 240y ≤ 5760
व्यापारी के पास सामान रखने के स्थान के अनुसार
x + y ≤ 20
व्यापारी द्वारा x पंखों का अर्जित लाभ = Rs 22x
तथा y सिलाई मशीनों पर अर्जित लाभ = Rs 18y
अत: अधिकतम लाभ अर्जित करने के लिये उद्देश्य फलन
Z = 22x + 18y
दी गई रैखिक प्रोग्रामन समस्या का गणितीय सूत्रीकरण निम्न प्रकार है–
अधिकतम Z = 22x + 18y
व्यवरोध 360x + 240y ≤ 5760
x + y ≤ 20
x ≥ 0, y ≥ 0
व्यवरोध के रूप में दी गई असमिकाओं को समीकरण में व्यक्त करने पर
360x + 240y = 5760
⇒ 3x + 2y = 48 …(1)
तथा x + y = 20 ..(2)
असपिका 360x + 240y ≤ 5760 द्वारा प्रदर्शित क्षेत्र –
रेखा 3x + 2y = 48 निर्देशी अक्षों को क्रमश: बिंदु A(16, 0) तथा B(0, 24) पर मिलती है।
3x + 2y = 480 के मान के लिए सारणी
| x | 16 | 0 |
| y | 0 | 24 |
A(16, 0); B(0, 24)
बिंदु A तथा B को अंकित कर रेखा का आलेख खींचते हैं।
असमिका में भूल बिंदु (0, 0) प्रतिस्थापित करने पर 3(0) + 2(0) = 0 ≤ 48 अपमिका को सन्तुष्ट करता है। अतः समस्या का हल क्षेत्र मूल बिंदु की ओर है।
असमिका x + y ≤ 20 द्वारा प्रदर्शित क्षेत्र –
रेखा x + y = 20 निर्देशी अक्षों को क्रमशः बिंदु C(20, 0) तथा D(0, 20) को मिलती है।
x + y = 20 के मानों के लिए सारणी
| x | 20 | 0 |
| y | 0 | 20 |
C(20, 0); D(0, 20)
बिंदु C तथा D को अंकित कर रेखा का आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) को प्रति स्थापित करने पर 0 + 0 = 0 ≤ 20 असमिका को सन्तुष्ट करता है।
अतः असमिका को हल मूल बिंदु की ओर होगा।
x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र –
चूँकि प्रथम पाद का प्रत्येक बिंदु असमिकाओं x ≥ 0 तथा y ≥ 0 को सन्तुष्ट करता है। अत: असमिका का हल प्रथम पाद है।
रेखाओं 3x + 2y = 480 तथा x + y = 20 के प्रतिच्छेद बिंदु के निर्देशांक x = 8 तथा y = 12 अतः प्रतिच्छेद बिंदु E(8, 12) है।
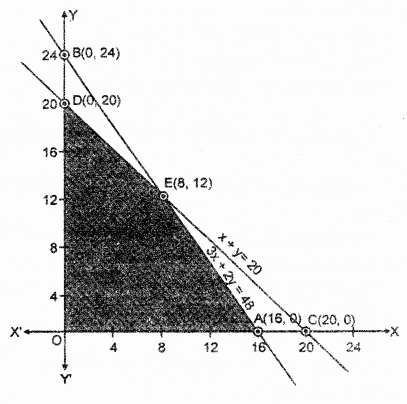
छायांकित क्षेत्र OAED उपरोक्त असमिकाओं का उभयनिष्ठ क्षेत्र प्रदर्शित करता है। यह क्षेत्र दी गई रैखिक समस्या का सुसंगत हल है। इस क्षेत्र के कोनीय बिंदुओं के निर्देशांक O(0, 0), A(16, 0), E(8, 12) तथा D(0, 20) हैं। जहाँ E रेखाओं 3x + 2y = 48 तथा x + y = 20 का प्रतिच्छेद बिंदु है।
इन बिंदुओं पर उद्देश्य फलन के मान नीचे सारणी में दिये गये हैं।
| बिन्द | x निर्देशांक | y निर्देशांक | उदेश्य फ्लन Z=22x+18y |
| O | 0 | 0 | ZO = 22×0+18×0 = 0 |
| A | 16 | 0 | ZA = 22×16+18×0 = 352 |
| E | 8 | 12 | ZE = 22×8+18×12 = 392 |
| D | 0 | 20 | ZD = 22×0+18×20 = 360 |
सारणी से स्पष्ट है कि उद्देश्य फलन का मान बिंदु E(8, 12) पर अधिकतम Rs 392 है।
अतः व्यापारी को अधिकतम लाभ अर्जित करने के लिये 8 पंखे तथा 12 सिलाई मशीन खरीदना चाहिये।
प्रश्न 6.
एक कारखाना दो प्रकार के पेचों A तथा B का उत्पादन करता है। प्रत्येक के उत्पादन के लिए दो प्रकार के यंत्रों स्वचालित तथा हस्तचालित की आवश्यकता होती है। एक पैकेट पेचों A के उत्पादन में 4 मिनट स्वचालित तथा 6 मिनट हस्तचालित मशीन तथा एक पैकेट पेचों B के उत्पादन में 6 मिनट स्वचालित तथा 3 मिनट हस्तचालित मशीन का कार्य होता है। प्रत्येक मशीन किसी भी दिन के लिये अधिकतम A घण्टे कार्य के लिए उपलब्ध है। निर्माता पेंच A के प्रत्येक पैकेट पर 70 पैसे तथा पेंच B के प्रत्येक पैकेट पर Rs 1 का लाभ कमाता है। यह मानते हुए कि कारखानों में निर्मित सभी पेचों के पैकेट बिक जाते हैं, निर्माता को प्रतिदिन प्रत्येक प्रकार के कितने पैकेट बनाने चाहिये जिससे अधिकतम लाभ अर्जित हो सके।
हल :
माना निर्माता को प्रतिदिन A पेचों के x पैकिट तथा B पेचों के y पैकिट बनाने चाहिये।
अतः x पैकेट पेच का लाभ = Rs 0.70x
तथा y पैकेट पेचों का लाभ = Rs y
अत: अधिकतम लाभ अर्जित करने के लिये उद्देश्य फलन
Z = 0.70x + y
A प्रकार के x पेचों को स्वचालित मशीन से बनाने का समय = 4x मिनट
तथा B प्रकार के y पेचों को स्वचालित मशीन से बनाने का समय = 6y मिनट
अतः प्रश्नानुसार स्वचालित मशीन द्वारा प्रतिदिन बनने वाले पैचों में लगा समय = 4x + 6y मिनट
परन्तु स्वचालित मशीन केवल चार घंटे ही उपलब्ध होती है । अतः
व्यवरोध 4x + 6y ≤ 4 x 60 मिनट
4x + 6y ≤ 240 मिनट
इसी प्रकार A प्रकार के पेच को हस्तचालित मशीन द्वारा बनाने में लगा समय = 6x मिनट
तथा B प्रकार के पेचों को हस्तचालित मशीन से बनाने में लगा समय = 3y मिनट
परन्तु हस्तचालित मशीन केवल 4 घंटे ही उपलब्ध होती है।
अतः व्यवरोध 6x + 3y ≤ 4 x 60 मिनट
⇒ 6x + 3y ≤ 240 मिनट
∵x और y पेचों की संख्या है।
∴x ≥ 0 तथा y ≥ 0
दी गई रैखिक प्रोग्रामिन समस्या का गणितीय सूत्रीकरण निम्न है-
अधिकतम
z = 0.70x + y
व्यवरोध 4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 0, y ≥ 0
व्यवरोधों के रूप में दी गई सभी असमिकाओं को समीकरण में । परिवर्तित करने पर,
4x + 6y = 240 …(1)
6x + 3y = 240 …(2)
असमिका 4x + 6y ≤ 240 द्वारा प्रदर्शित क्षेत्र –
रेखा 4x + 6y = 240 निर्देशी अक्षों को क्रमशः बिंदु A(60, 0) तथा B(0, 40) पर मिलती
4x + 6y = 240 के मानों के लिए सारणी
| x | 60 | 0 |
| y | 0 | 40 |
बिंदु A और B को अंकित कर आलेख खींचते हैं।
असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 4(0) + 6(0) = 0 ≤ 240 असमिका को सन्तुष्ट करता है। अत: असमिका का हल क्षेत्र मूल बिंदु की ओर होगा ।
असमिका 6x + 3y ≤ 240 द्वारा प्रदर्शित क्षेत्र –
देखा 6x + 3y = 240 निर्देशी अक्षों को क्रमशः बिंदु C(40,0) तथा D(0, 80) पर मिलती
6x + 3y = 240 के दानों के लिए सारणी
| x | 40 | 0 |
| y | 0 | 80 |
C(40, 3); D(0, 80)
बिंदु C और D को अंकित कर रेखा का आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) प्रतिस्थापित करने पर 6(0) + 3(0) = 0 ≤ 240 असमिका को सन्तुष्ट करता है। अतः असमिका का हल क्षेत्र मूल | बिंदु की ओर होगा।
x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र –
चूँकि प्रथम पाद में प्रत्येक बिंदु इन दोनों असमिकाओं को सन्तुष्ट करता है। अतः असभिकाओं x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र प्रथम पाद है।
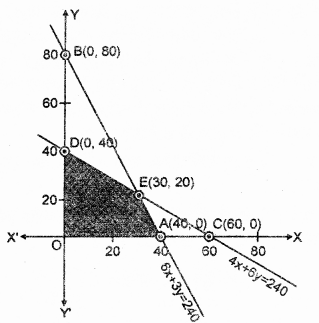
रेखाओं 4x + 6y = 240 तथा 6x + 3y = 240 के प्रतिच्छेद बिंदु के निर्देशांक x = 30 तथा y = 20 है।।
छायांकित क्षेत्र OAED उपरोक्त असमिकाओं का उभयनिष्ठ क्षेत्र प्रदर्शित करता है। यह क्षेत्र दी गई खिक प्रोग्रामन समस्या का सुसंगत हल क्षेत्र हैं।
इस हल क्षेत्र के कोनीय बिंदुओं के निर्देशांक O(0, 0), A(40, 0), E(30, 20) तथा D(0, 40) हैं।
इन बिंदुओं पर उद्देश्य फलन के मान नीचे सारणी में दिये गये हैं-
| बिन्द | x निर्देशांक | y निर्देशांक | उदेश्य फ्लन Z=0.70x+y |
| O | 0 | 0 | ZO = 0.70×0+0 = 0 |
| A | 40 | 0 | ZA = 0.70×40+0 = 28 |
| E | 30 | 20 | ZE = 0.70×30+20 = 41 |
| D | 0 | 40 | ZD = 0.70×0+40 = 40 |
सारणी से स्पष्ट है कि उद्देश्य फलन का मान बिंदु E(30, 20) पर अधिकतम Rs 41 है।
अतः निर्माता को पेंच A के 30 पैकेट तथा पेच B के 20 पैकेट बनाने चाहिये ताकि उसे अधिकतम लाभ Rs 41 प्राप्त हो सके।
प्रश्न 7.
एक फर्म प्लाईवुड के अनूठे स्मृति चिन्ह का निर्माण करती है A प्रकार के प्रत्येक स्मृति चिन्ह के निर्माण में 5 मिनट काटने तथा 10 मिनट जोड़ने में लगते हैं। B प्रकार के प्रत्येक स्मृति चिन्ह के निर्माण में 8 मिनट काटने तथा 8 मिनट जोड़ने में लगते है। काटने तथा जोड़ने के लिये कुल समय क्रमशः 3 घण्टे 20 मिनट तथा 4 घण्टे उपलब्ध है। फर्म को प्रत्येक A प्रकार के स्मृति चिन्ह पर Rs 5 तथा प्रत्येक B प्रकार के स्मृति चिन्ह पर Rs 6 का लाभ होता है। अधिकतम लाभ प्राप्त करने के लिए फर्म को प्रत्येक प्रकार के कितने-कितने स्मृति चिन्हों का निर्माण करना चहिये?
हल :
माना फर्म को A प्रकार के x स्मृति चिन्ह तथा B प्रकार के y स्मृति चिन्ह बनाने चाहिये।
इसलिये x स्मृति चिन्हों पर अर्जित लाभ = Rs 5x
तथा y स्मृति चिन्हों पर अर्जित लाभ = Rs 6y
अत: अधिकतम लाभ अर्जित करने के लिये उद्देश्य ‘फलन की
मान z = 5x + 6y
चूँकि A प्रकार के स्मृति चिन्ह को काटने में लगा समय
= 5x मिनट
तथा B प्रकार के स्मृति चिन्हों को काटने में लगा समय = 8y मिनट
अतः प्रश्नानुसार A और B प्रकार के स्मृति चिों को काटने में लगे कुल समय के लिये
व्यवरोध 5x + 8y ≤ 3 घंटे 20 मिनट
⇒5x + 8y ≤ 200 मिनट
इसी प्रकार A तरह के स्मृति चिह्नों को जोड़ने में लगा समय
= 10x मिनट
तथा B तरह के स्मृति चिों को जोड़ने में लगा समय
= 8y मिनट
अत: प्रश्नानुसार A और B प्रकार के स्मृति चिों को जोड़ने में लगे कुल समय के लिये,
व्यवरोध 10x + 8y ≤ 4 घंटे
⇒ 10x + 8y ≤ 240 मिनट
अतः दी गई रैखिक प्रोग्रासन समस्या का गणितीय सूत्रीकरण निम्न
अधिकतम
z = 5x + 6y
व्यवरोध 5x + 8y ≤ 200
10x + 8y ≤ 240
तथा x ≥ 0, y ≥ 0
व्यवरोधों के रूप में दी गई असमिकाओं को समीकरण रूप में परिवर्तित करने पर,
5x + 8y = 200 …(1)
10x + 8y = 240 …(2)
असमिका 5x + 8y ≤ 200 द्वारा प्रदर्शित क्षेत्र – रेखा 5x + 8y = 200 निर्देशी अक्षों को क्रमशः बिंदु A(40, 0) तथा B(0, 25) पर मिली
5x + 8y = 200 के भानों के लिए सारणी
| x | 40 | 0 |
| y | 0 | 25 |
A(40, 0); B(0, 25) बिंदुओं A और B को अंकित कर रेखा का आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 5(0) + 8(0) = 0 ≤ 200 असमिका सन्तुष्ट होती है। अतः असमिका को हल क्षेत्र भूल बिंदु की ओर होगा।
असमिको 10x + 8y ≤ 240 द्वारा प्रदर्शित क्षेत्र – रेखा 10x + 8y = 240 निर्देशी अक्षों को बिंदु C(24, 0) तथा D(0, 30) पर मिलती है।
10x + 8y = 240 के मानों के लिए सारणी
| x | 24 | 0 |
| y | 0 | 30 |
C(24, 0); D(0, 30)
बिंदुओं C और D को अंकित कर आलेख खचते हैं। असमिका में भूलविंदु को प्रतिस्थापित करने पर 10(0) + 8(0) = 0 ≤ 240 असमिका सन्तुष्ट होती है। अत: असमिका का हल क्षेत्र मूल बिंदु की ओर होगा।
x ≥ 0, y ≥ द्वारा प्रदर्शित क्षेत्र – चूँकि प्रथम पाद का प्रत्येक बिंदु इन दोनों असमिकाओं को सन्तुष्ट करता है। अत: उस समकाओं x ≥ 0, y ≥ 0 द्वारा प्रदर्शित क्षेत्र प्रथम पाद हो ।
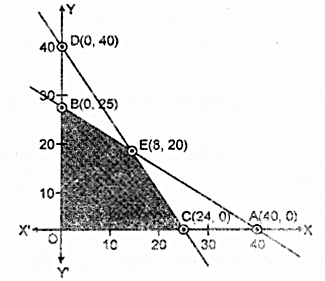
रेखाओं 5x + 8y = 200 तथा 10x + 8y = 240 के प्रतिच्छेद बिंदु E के निर्देशांक x = 8, y = 20 है।।
छायांकित क्षेत्र OCEB उपरोक्त असमिकाओं का उभयनिष्ठ क्षेत्र प्रदर्शित करता है। यह क्षेत्र दी गई रैखिक प्रोग्रामन समस्या का सुसंगत हल है। इस हल क्षेत्र के कोनीय बिंदुओं के निर्देशांक O(0, 0), C(24, 0), E(8, 20) तथा B(0, 25) है।
इन बिंदुओं पर उद्देश्य फ लन का मान अग्र सारणी में दिया गया
| बिन्द | x निर्देशांक | y निर्देशांक | उदेश्य फ्लन Z=5x+6y |
| O | 0 | 0 | ZO = 5×0+6×0 = 0 |
| C | 24 | 0 | ZC =5×24+6×0 = 120 |
| E | 8 | 20 | ZE = 5×8+6×20 = 160 |
| B | 0 | 25 | ZB = 5×0+6×25 = 150 |
सारिणी से स्पष्ट है कि बिंदु E(8, 20) पर उद्देश्य फलन का मान अधिकतम Rs 160 है। अत: अधिकतम लाभ प्राप्त करने के लिये फर्म को A प्रकार के 8 तथा B प्रकार के 20 स्मृति चिह्न बनाने चाहिये।
प्रश्न 8.
एक किसान के पास दो प्रकार के उर्वरक F1 व F2 है। उर्वरक F1 में 10% नाइट्रोजन तथा 6% फॉस्फोरिक अम्ल है। जबकि उर्वरक F2 में 5% नाइट्रोजन तथा 10% फॉस्फोरिक अम्ल हैं। मिट्टी की स्थितियों का परीक्षण करने के बाद किसान पाता है कि उसे अपनी फसल के लिए कम से कम 14 किलोग्राम नाइट्रोजन तथा कम से कम 14 किलोग्राम फॉस्फोरिक अमन की आवश्यकता है। यदि उर्वरक F1 की कीमत 60 पैसे प्रति किलोग्राम तथा F2 की कीमत 40 पैसा प्रति किलोग्राम हो तो न्यूनतम मूल्य र वाछित पोषक तत्वों की आवश्यकता को ध्यान में रखते हुए प्रत्येक बैरक की कितनी किलोग्राम मात्रा उपयोग में लाई जानी चाहिये।
हल :
माना F1 उर्वरक की मात्रा x किग्रा. तथा F2 की मात्रा y किग्रा. है।
चूँकि F1 उर्वरक की कीमत 60 पैसे प्रति किग्रा तथा F2 उर्वरक की कीमत 40 पैसे प्रति किग्रा है।

अतः न्यूनतम मूल्य पर वांछित पोषक तत्वों की कुल कीमत का उद्देश्य फलन

व्यवरोधों के रूप में दी गई असमिकाओं को समीकरण में बदलने
10x + 5y = 1400 …(1)
6x + 10y = 1400 …(2)
x = 0 …(3)
y = 0 …(4)
असमिका
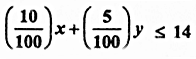
द्वारा प्रदर्शित क्षेत्ररेखा 10x + 5y = 1400 निर्देशी अक्षों को क्रमशः बिंदु A(140, 0) तथा B(280, 0) पर मिलते हैं।
10x + 5y = 1400 के मानों के लिए सारणी
| x | 140 | 0 |
| y | 0 | 280 |
A(140, 0); B(0, 280)
A और B को अंकित कर रेखा का आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 10(0) + 5(0) = 0 ≤ 1400 असमिका सन्तुष्ट होती है। अत: असमिका का हल क्षेत्र मूल बिंदु की। ओर होगा।
असमिका
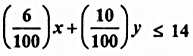
द्वारा प्रदर्शित क्षेत्र-
रेखा 6x + 10y = 1400 निर्देशी अक्षों को क्रमशः बिंदु C(\(\frac { 1400 }{ 6 }\), 0)।
तथा D(0, 140) पर मिलती है।
6x + 10y = 1400 के मानों के लिए सारणी
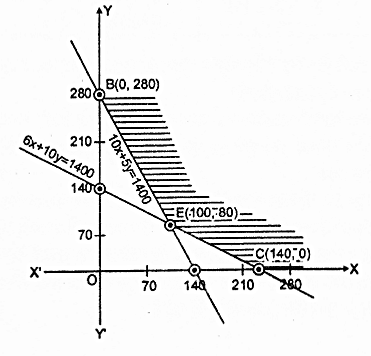
C(\(\frac { 1400 }{ 6 }\), 0): D(0, 140)
इन बिंदुओं को अंकित कर रेखा का आलेख खींचते हैं। असमिको में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 6(0) + 10(0) = 0 ≤ 1400 असमिका सन्तुष्ट होती है। अत: असमिका को हल क्षेत्र मूल बिंदु की ओर होगा।
x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र –
चूँकि प्रथम पद में प्रत्येक बिंदु इन दोनों असमिकाओं को सन्तुष्ट करता है अतः इन असमिकाओं का हल क्षेत्र प्रथम पाद है।
रेखाओं 10x + 5y = 1400 तथा 6x + 10y = 1400 के प्रतिच्छेद
बिंदु E के निर्देशांक x = 100 तथा y = 80 हैं।
छायांकित धोत्र CEB उपरोक्त असमिकाओं का उभयनिष्त क्षेत्र है। यह क्षेत्र दी गई रैखिक प्रोग्रामन समस्या का सुसंगत हल क्षेत्र है। इस क्षेत्र के कोनीय बिंदुओं के निर्देशांक C(\(\frac { 1400 }{ 6 }\), 0), E(100, 8) तथा B(0, 280) हैं।
इन बिंदुओं पर उद्देश्य फलन के मान नीचे सारिणी में दिये गये हैं-
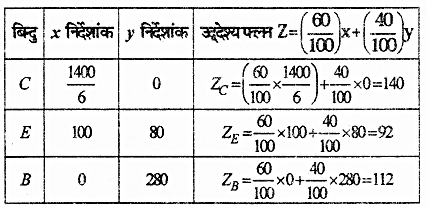
सारणी से स्पष्ट है कि उद्देश्य फलन का मान बिंदु E(100, 80) पर न्यूनतम है। अतः न्यूनतम मूल्य पर उर्वरकों की मात्रा क्रमशः 100 किग्रा, तथा 80 किग्रा होनी चाहिये। न्यूनतम मूल्य Rs 92 है।
प्रश्न 9.
एक व्यापारी दो प्रकार के निजी कम्प्यूटर एक डेस्कटॉप प्रतिरूप तथा एक पोर्टेबल प्रतिरूप जिनकी कीमतें क्रमशः Rs 25,000 तथा Rs 40,000 होगी, बेचने की योजना बनाता है। वह अनुमान लगाता है कि कम्प्यूटर की कुल मासिक प्रांग 250 इकाइयों से अधिक नहीं होगी। प्रत्येक प्रकार के कम्प्यूटरों की इकाईयों की संख्या ज्ञात कीजिये जिसे व्यापारी अधिकतम लाभ प्राप्त करने के लिए भण्डारण करें यदि उसके पास निवेश करने के लिए Rs 70 लाख से अधिक नहीं है तथा यदि व्यापारी का डेस्कटॉप प्रतिरूप पर लाभ Rs 4500 तथा पोर्टेबल प्रतिरूप पर लाभ Rs 5000 से।
हल :
माना डेस्कटॉप प्रतिरूप की मात्रा x तथा पोर्टेबल प्रतिरूप की मात्रा y है।
अतः अधिकतम लाभ प्राप्त करने के लिये उद्देश्य फलन
z = 4500x + 5000y
कम्प्यूटरों की कुल संख्या x + y ≤ 250 चूँकि कुल मासिक माँग 250 इकाइयों से अधिक नहीं है।
कम्प्यूटरों की कुल कीमत 25000x + 40000y ≤ 70,000,00
चूंकि x और y कम्प्यूटरों की संख्या है इसलिये –
x ≥ 0, y ≥ 0
अतः दी गई रैखिक प्रोग्रामन समस्या का गणितीय सूत्रीकरण निम्न
अधिकतम z = 4500x + 5000y
व्यवरोध x + y ≤ 250
25000x + 40,000y ≤ 70,000,00
x ≥ 0, y ≥ 0
व्यवरोधों में रूप में दी गई असमिकाओं को समीकरण में परिवर्तित करने पर
x + y = 250 …(1)
25000x + 40000y = 70,000,00
25x + 40y = 7000 …(2)
x = 0 …(3)
y = 0 …(4)
असमिका x + y ≤ 250 द्वारा प्रदर्शित क्षेत्र –
रेखा x + y = 250 निर्देशी अक्षों को क्रमशः बिंदु A(250, 0) तथा B(0, 250) पर मिलती
x + y = 250 के मानों के लिए सारणी
| x | 250 | 0 |
| y | 0 | 250 |
A(250, 0); B(0, 250)
बिंदुओं A तथा B को अंकित कर आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 0 + 0 = 0 ≤ 250 असमिका सन्तुष्ट होती है। अतः असमिका का हल क्षेत्र मूल बिंदु की ओर होगा।
असमिका 25x + 40y ≤ 7000 द्वारा प्रदर्शित क्षेत्र –
रेखा 25x + 40y = 7000 निर्देशी अक्षों को क्रमशः बिंदु C(280, 0) तथा D(0, 175) पर मिलती है।
25x + 40y = 7000 के मानों के लिए सारणी
| x | 280 | 0 |
| y | 0 | 175 |
C(280, 0); D(0, 175)
बिंदुओं C और D को अंकित कर रेखा का आलेख खचते हैं। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर
25(0) + 40(0) = 0 ≤ 7000 असमिका सन्तुष्ट होती है। अत: इस असमिका का हल क्षेत्र मूल बिंदु की ओर होगा।
x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र –
चूँकि प्रथम पद में प्रत्येक बिंदु इन दोनों असमिकाओं को सन्तुष्ट करता है। अतः असमिकाओं का हल क्षेत्र प्रथम पाद है।
रेखाओं x + y = 250 तथा 25x + 40y = 7000 के प्रतिच्छेद बिंदु E के निर्देशांक x = 200 तथा y = 50 है।
छायांकित क्षेत्र OAED उपरोक्त असमिकाओं का उभयनिष्ठ क्षेत्र है। यह क्षेत्र की गई रैखिक प्रोग्रामन समस्या का सुसंगत हल क्षेत्र है। इस क्षेत्र के कोनीय बिंदुओं के निर्देशांक O(0, 0), A(250, 0), E(200, 50) तथा D(0, 175) है।
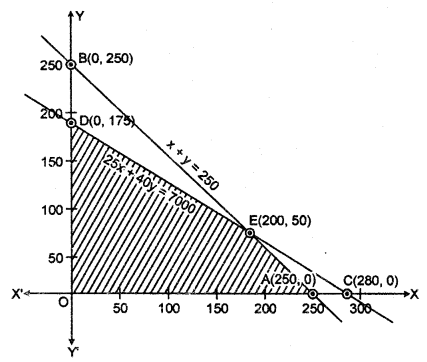
इन बिंदुओं पर उद्देश्य फलन का मान नीचे सारणी में दिये गये
| बिन्द | x निर्देशांक | y निर्देशांक | उदेश्य फ्लन Z = 4500x + 5000y |
| O | 0 | 0 | ZO = 4500 x 0 + 5000 x 0 = 0 |
| A | 250 | 0 | ZA = 4500 x 250 + 5000 x 0 = 11,25,000 |
| E | 200 | 50 | ZE = 4500 x 200 + 5000 x 50 = 900000 + 250000 = 1150000 |
| D | 0 | 175 | ZD = 4500 x 0 + 5000 x 175 = 8,75,000 |
सारणी से स्पष्ट है कि उद्देश्य फलन का मान बिंदु E(200, 50) पर Rs 11,50,000 है।
अतः व्यापारी को अधिकतम लाभ कमाने के लिये डेस्कटॉप कम्प्यूटर 200 तथा पोर्टेबल कम्प्यूटर 50 खरीदने चाहिये। अधिकतम लाभ = Rs 11,50,000
प्रश्न 10.
दो अन्न भण्डारों A तथा B की भण्डारण क्षमता क्रमशः 100 क्विण्टल तथा 50 क्विटल है। उन्हें तीन राशन की दुकानों D, E तथा F पर अन्न उपलब्ध करवाना है, जिनकी आवश्यकताएँ क्रमशः 60, 50 तथा 40 क्विटल है। भण्डारों से दुकानों को प्रति क्विटल परिवहन लागत निम्न सारणी में दी गई है।
सारणी
| को \ से | प्रति क्विंटल परिवहन लागत (Rs में) | |
| A | B | |
| D | 6 | 4 |
| E | 3 | 2 |
| F | 2.50 | 3 |
परिवहन लागत के निम्नतमीकरण के लिये आपूर्ति का परिवहन कैसे किया जाए ?
हल :
माना भण्डार A से D को x किंवटल तथा दुकान E को y किंवटल राशन भेजा जाता है तो शेष राशन (100 – x – y) किंवटल राशन दुकान F को भेजा जायेगा।
अतः सारणी के अनुसार भण्डार A से दुकान D तक परिवहन लागत = Rs 6x
दुकान E तक की परिवहन लागत = Rs 3y
तथा दुकान F तक की परिवहन लागत
= Rs \(\frac { 5 }{ 2 }\)(100 – x – y)
अतः भण्डार A से दुकान D, E तथा F तक राशन पहुँचाने की लागत
= 6x + 3y + \(\frac { 5 }{ 2 }\)(100 – x – y)
दुकान D की शेष आपूर्ति (60 – x) किंवटल, E थी।
शेष आपूर्ति (50 – y) किंवटल तथा दुकान F की शेष आपूर्ति [40 – (100 – x – y)] क्विंटल, भण्डार B से की जाती है, अतः सारणी अनुसार भण्डार
B से दुकान D की परिवहन लागत = Rs 4(60 – x)
दुकान E की परिवहन लागत = Rs 2(50 – y)
तथा F की परिवहन लागत = Rs 3(x + y – 100)
अतः भण्डार B से दुकानें D, E तथा F तक की लागत ।
= 4(60 – x) + 2(50 – y) + 3(x + y – 60)
अत: दोनों भण्डारों A और B से दुकानों D, E तथा F तक की कुल परिवहन लागत
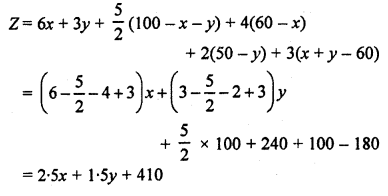
भण्डार A की कुल क्षमता 100 क्विटल है; अतः
x + y ≤ 100
दुकान D को भण्डार A से x क्विंटल तथा शेष भण्डार B से मिलता हैं; अतः
x ≤ 60
इसी प्रकार दुकान E को भण्डार A से y क्विंटल तथा शेष भण्डार B से मिलता है; अतः
y ≤ 50
इसी प्रकार दुकान F को भण्डार A से (100 – x – y) किंवटल तथा शेष भण्डार B से मिलता है
x + y ≥ 60
तथा x ≥ 0 तथा y ≥ 0
चूँकि x और y राशन की मात्रा किंवटलों में है।
अतः दी गई रैखिक प्रोग्रामन समस्या का गणितीय सूत्रीकरण निम्न प्रकार है।
निम्नतकीकरण z = 2.5x + 1.5y + 410
व्यवरोध
x + y ≤ 100
x ≤ 60
y ≤ 50
x + y ≥ 60
x ≥ 0, y ≥ 0
दिये गये व्यवरोध को असमिकाओं से समीकरण में परिवर्तित करने
पर x + y = 100 ..(1)
x = 60 ….(2)
y = 50 ….(3)
x + y = 60 …(4)
x = 0 …(5)
y = 0 …(6)
असमिका x + y ≤ 100 द्वारा प्रदर्शित क्षेत्र –
रेखा x + y = 100 निर्देशी अक्षों को क्रमशः बिंदु की (100, 0) तथा बिंदु B(0, 100) पर मिलती है।
x + y = 100 के मानों के लिए सारणी
| x | 100 | 0 |
| y | 0 | 100 |
A(100, 0); B(0, 100)
बिंदु A और B को अंकित कर रेखा का आलेख खचते हैं।
असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर असमिका 0 + 0 = 0 ≤ 100 सन्तुष्ट होती है। अतः असमिका का हल मुल बिंदु की ओर होगा।
असमिका x ≤ 60 द्वारा प्रदर्शित क्षेत्र – रेखा x = 60 निर्देशी अक्षों को क्रमशः C(60, 0) तथा D(60, 50) पर मिलती है।
x + 0.y = 60 के मानों के लिए सारणी
| x | 60 | 60 |
| y | 0 | 50 |
C(60, 0); D(60, 5)
बिंदुओं C और D को अंकित कर रेखा का आलेख खींचते हैं। असमिका को मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 0 + 0 = 0 ≤ 60 असमिका सन्तुष्ट होती है। अत: असमिका का हल मूल बिंदु की और होगा।
असमिका y ≤ 50 द्वारा प्रदर्शित क्षेत्र – रेखा y = 50 अक्षों को क्रमशः बिंदु E(0, 50) तथा F(5, 50) पर मिलती है।
0.x + y = 50 के मानों के लिए सारणी
| x | 0 | 50 |
| y | 50 | 50 |
E(0, 50); F(50, 50)
बिंदुओं E और F को अंकित कर रेखा का आलेख ख़चते हैं। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 0 + 0 ≤ 50 असमिका सन्तुष्ट होती है। अतः असमिका का हल क्षेत्र मूल बिंदु की और होगा।
असमिका x + y ≥ 60 द्वारा प्रदर्शित क्षेत्र –
रेखा x + y = 60 निर्देशी अक्षों को क्रमशः बिंदु G(60, 0) तथा H(0, 60) पर मिलती है।
x + y = 60 के मानों के लिए सारणी
| x | 60 | 0 |
| y | 0 | 60 |
G(60, 0); H(0, 60)
बिंदुओं G और H को अंकित कर रेखा का आलेख खींचते हैं। असमिका में मूल बिंदु (0, 0) को प्रतिस्थापित करने पर 0 + 0 = 0 ≥ 60 । अतः असमिका सन्तुष्ट नहीं होता है। इसलिये असमिका का हल क्षेत्र मूल बिंदु के विपरीत ओर होगा।
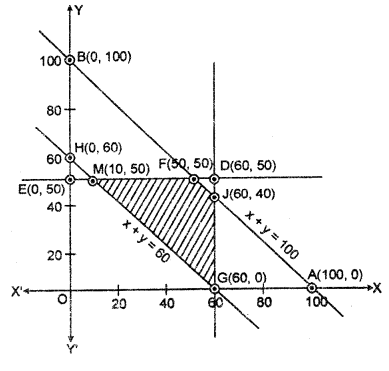
x ≥ 0 तथा y ≥ 0 द्वारा प्रदर्शित क्षेत्र –
चूँकि प्रथम पाद का प्रत्येक बिंद x ≥ 0 तथा y ≥ 0 को सन्तुष्ट करता है। अतः असमिकाओं का हल क्षेत्र प्रथम पाद ही होगा।
छायांकित क्षेत्र GJFM उपरोक्त असमिकाओं का उभयनिष्ठ क्षेत्र प्रदर्शित करता है। यह क्षेत्र दी गई रैखिक प्रोग्रामन समस्या का सुसंगत हल क्षेत्र है। छायांकित सुसंगत हल क्षेत्र के कोनीय बिंदुओं के निर्देशांक G(60, 0), J(40, 60), F(50, 50) तथा M(10, 50) है जहाँ बिंदु J रेखाओं x + y = 100 तथा x = 60 का प्रतिच्छेद बिंदु, F रेखा x + y = 100 तथा y = 100 का प्रतिच्छेद बिंदु तथा M रेखा x + y = 60 तथा y = 50 का प्रतिच्छेद बिंदु है।
इन बिंदुओं पर उद्देश्य फलन के मान नीचे सारिणी में दिये गये हैं।
| बिन्द | x निर्देशांक | y निर्देशांक | उदेश्य फ्लन Z=45000x+5000y |
| G | 60 | 0 | ZG = 2.5(60)+1.5(0)+410 = 560 |
| J | 40 | 60 | ZJ = 2.5(40)+1.5(60)+410 = 600 |
| F | 50 | 50 | ZF = 2.5(50)+1.5(50)+410 = 610 |
| M | 10 | 50 | ZM = 2.5(10)+1.5(50)+410 = 510 |
सारणी से स्पष्ट है कि उद्देश्य फलन का मान बिंदु M(10, 50) पर न्यूनतम Rs 510 है।
अत; निम्नतम परिवहन लागत के लिये भण्डार A से D, E और F दुकानों को क्रमशः 10, 50 व 40 किंवटल तथा भण्डार B से D, E तथा F दुकानों को 50, 0, 0 क्विंटल भेजना होगा।