RBSE Solutions for Class 6 Maths Chapter 12 Algebra Additional Questions is part of RBSE Solutions for Class 6 Maths. Here we have given Rajasthan Board RBSE Class 6 Maths Chapter 12 Algebra Additional Questions.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 6 |
| Subject | Maths |
| Chapter | Chapter 12 |
| Chapter Name | Algebra |
| Exercise | Additional Questions |
| Number of Questions | 16 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 6 Maths Chapter 12 Algebra Additional Questions
Multiple Choice Questions
Question 1.
Value of n, which (RBSESolutions.com) satisfy equation 2n = 4 will be
(i) 5
(ii) 4
(iii) 3
(iv) 2
Question 2.
Value of x, which satisfy equation 2x = 20 will be
(i) 2
(ii) 3
(iii) 4
(iv) 5
![]()
Question 3.
Value of p, which satisfy (RBSESolutions.com) equation 5p – 3 = 2, will be
(i) 0
(ii) 1
(iii) 2
(iv) 3
Question 4.
If side of square is l, then its perimeter will be
(i) \(\frac { l }{ 4 } \)
(ii) 4l
(iii) 3l
(iv) 5l
Question 5.
Sonu is 7 years younger than Monu. If Monu is x years old, then age of Sonu will be
(i) 7x
(ii) x – 7
(iii) x + 7
(iv) 7x +7
Question 6.
Related variable (RBSESolutions.com) in equation : x + 70 = 20 is
(i) 20
(ii) n
(iii) 70
(iv) x
Answers:
1. (iv)
2. (iii)
3. (ii)
4. (ii)
5. (ii)
6. (iv)
Question 1.
Fill in the blanks :
(i) An equation has ……………. sides.
(ii) The value (RBSESolutions.com) of variable in an equation which satisfies the equation is called ……………. to the equation.
(iii) The value of a variable is not ……………. .
Answer:
(i) two
(ii) a solution
(iii) fixed.
![]()
Very Short Answer Type Questions
Question 1.
Solve the equation x + 5 = 10
Solution:
On adding (- 5) or subtracting (+ 5) from both sides
x + 5 + (- 5) = 10 + (- 5)
⇒ x = 10 – 5 ⇒ x = 5
Question 2.
Solve the (RBSESolutions.com) equation 5x = 45
Solution:
5x = 45
Multiply both sides by \(\frac { 1 }{ 5 } \)
\( 5x\times \frac { 1 }{ 5 } \)
= \( 45\times \frac { 1 }{ 5 } \)
⇒ x = 9
Question 3.
Solve the equation \(\frac { p }{ 4 }=2\)
Solution:
\(\frac { p }{ 4 }=2\)
Multiply both sides by 4,
⇒ \(\frac { p }{ 4 } \times 4\) = 2 × 4
⇒ P = 8.
Question 4.
Solve the (RBSESolutions.com) equation x – 7 = 15
Solution:
x – 7 = 15
Add 7, both sides
x – 7 + 7 = 15 +7
⇒ x = 22
Question 5.
Which of the following (RBSESolutions.com) expressions have only numbers ?
(a) y + 3
(b) 7 × 20 – 8z
(c) 5 (21 – 7) + 7 × 2
(d) 5
(e) 3x
(f) 5 – 5n
(g) 7 × 20 – 5 × 10 – 45 + p
Solution:
expressions (c) and (d) has only numbers.
![]()
Question 6.
(a)Construct expressions using t and 4. Do not use more than (RBSESolutions.com) one number operation. ‘t’ is necessary in each expression.
(b) Construct expressions using y, 2 and 7. ‘y’ is necessary in each expression. Use only two number operations, which are different.
Solution:
(a) Possible expression, using t and 4
(i) t + 4
(ii) t – 4
(iii) \(\frac { t }{ 4 } \)
(iv) 4t
(v) \(\frac { 4 }{ t } \)
(vi) 4 – t
(b) Possible expression (RBSESolutions.com) using y, 2 and 7 (operate only two different numbers)
(i) 2y + 7
(ii) 2y – 7
(iii) 7y + 2
(iv) 7y – 2
(v) \(\frac { y }{ 2 } -7\)
(vi) \(\frac { y }{ 2 } +7\)
(vii) \(y+\frac { 7 }{ 2 } \)
(viii) \(y+\frac { 7 }{ 2 } \)
(ix) \(\frac { y }{ 7 } +2\) and \(\frac { y }{ 7 } -2\) e.t.c.
Short/Long Answer Type Questions
Question 1.
Convert following open (RBSESolutions.com) statement into equations
(i) While adding 3 in x, gives 11.
(ii) On subtraction x form 7, 12 remains.
(iii) Increasing a number by 10, we get 22.
(iv) 5 times of a number is 35.
(v) How much subtract form 15, to get 2 ?
Solution:
(i) Addition of 3 and x = x + 3 (LHS)
Real result = 11 (RHS)
Thus equation x + 3 = 11.
(ii) Subtracting 7 from x = x – 7 (LHS)
Real remainder = 12 (RHS)
Thus, equation x – 7= 12.
(iii) Increasing 10 in (RBSESolutions.com) number = x + 10 (LHS)
Real result = 22 (RHS)
Thus, equation x + 10 = 22.
(iv) Let number is x
Five times of number = 5x (LHS)
Product = 35 (RHS)
Thus, equation 5x = 35.
(v) Let x subtracted from 15
then Remainder = 15 – x (LHS)
Real remainder = 2 (RHS)
Thus, equation 15 – x = 2
Question 2.
Derive the statements (RBSESolutions.com) from following equations :
(a) z – 12
(b) r + 25
(c) 16p
(d) \(\frac { y }{ 8 } \)
(e) -9m
(f) 10y + 7
(g) 2n – 1
Solution:
(a) Subtraction of 12 from z
(b) Addition of r and 25
(c) Multiply of 16 in p
(d) y divided by 8
(e) Multiply of (-9) in m
(f) Addition of 7 in the product of n by 2
(g) Subtracting ‘l’ from the product of n by 2.
![]()
Question 3.
Following figures represents the pattern (RBSESolutions.com) of triangles constructed by matchsticks. Find the general rule which gives the number of required matchsticks in terms of number of triangles.
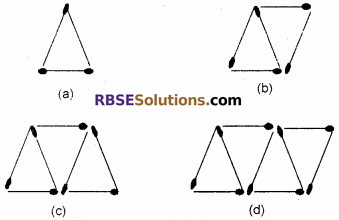
Solution:
image
∴ Rule is as follow :
number of matchsticks = 2x + 1, where x is number of triangles.
Question 4.
Complete the table and find the (RBSESolutions.com) solution of equation m – 7 = 3

Solution:
On completing given equation
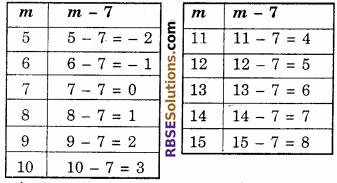
It is clear from (RBSESolutions.com) above table, that m = 10, satisfies equation m – 7 = 3
∴ m = 10 is solution of equation.
We hope the RBSE Solutions for Class 6 Maths Chapter 12 Algebra Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 6 Maths Chapter 12 Algebra Additional Questions, drop a comment below and we will get back to you at the earliest.