RBSE Solutions for Class 7 Maths Chapter 16 Perimeter and Area Ex 16.2

RBSE Solutions for Class 7 Maths Chapter 16 Perimeter and Area Ex 16.2 is part of RBSE Solutions for Class 7 Maths. Here we have given Rajasthan Board RBSE Class 7 Maths Chapter 16 Perimeter and Area Exercise 16.2.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 7
Subject	Maths
Chapter	Chapter 16
Chapter Name	Perimeter and Area
Exercise	Ex 16.2
Number of Questions	10
Category	RBSE Solutions

Rajasthan Board RBSE Class 7 Maths Chapter 16 Perimeter and Area Ex 16.2

Question 1
Find the area of parallelogram and triangle by (RBSESolutions.com) observing the following figures.

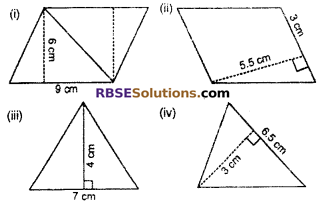
Solution:
(i) Base of parallelogram = 9 cm
Height of parallelogram = 6 cm
Area of parallelogram = Base x Height
= 9 x 6 = 54 sq. cm

(ii) Base of parallelogram = 3 cm
Height of (RBSESolutions.com) parallelogram = 5.5 cm
Area of parallelogram = Base x Height = 3 x 5.5
= 16.5 sq. cm

(iii) Base of triangle = 7 cm
Height of triangle = 4 cm
Area of triangle = \(\frac { 1 }{ 2 }\) x Base x Height 1 28
= \(\frac { 1 }{ 2 }\) x 7 x 4 = \(\frac { 28 }{ 2 }\) = 14 sq. cm

(iv) Base of triangle = 6.5 cm
Height of triangle = 3 cm
Area of triangle = \(\frac { 1 }{ 2 }\) x Base x Height
= \(\frac { 1 }{ 2 }\) x 6.5 x 3
= 6.5 x 1.5 = 9.75 sq. cm.

Question 2
The height of parallelogram is (RBSESolutions.com) one fourth of it’s base. If its area is 144 sq. cm then find its base and height.
Solution:
Let base of parallelogram = x cm
Height of parallelogram = \(\frac { x }{ 4 }\)
Area of parallelogram = 144 sq. cm
⇒ Base x Height = 144 x 4
x × \(\frac { x }{ 4 }\) = 144
x² = 144 × 4
x = \(\sqrt { 144\times 4 }\)
x = 12 x 2 = 24 cm
Base of parallelogram = 24 cm
Height of parallelogram = \(\frac { x }{ 4 }\) = \(\frac { 24 }{ 4 }\) = 6 cm.

Question 3
Area of triangular field of Kali and rectangular (RBSESolutions.com) field of Hamida are some. The length and breadth of Hamida’s are 20 cm and 15 cm. The length of base of Kali’s field is 25 cm then find height of it.
Solution:
Length of Hamida’s rectangular field = 20 cm
and breadth = 15 cm
Base of Kali’s triangular field = 25 cm
Area of triangluar = Area of Hamida’s rectangular shape field
⇒ \(\frac { 1 }{ 2 }\) x base x height = length x breadth
⇒ \(\frac { 1 }{ 2 }\) x 25 x height = 20 x 15
⇒ height = \(\frac { 20 \times 15 \times 2 }{ 25 }\) = 24 cm

Question 4
In triangle PQR (given figure) PQ = 4 cm, PR = 8 cm, RT = 6 cm then (RBSESolutions.com) find :
(i) Area of ∆PQR
(ii) Length of QS

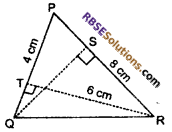
Solution:
In triangle PQR, PQ = 4 cm
PR = 8 cm and RT = 6 cm
(i) Area of ∆PQR = \(\frac { 1 }{ 2 }\) x Base x height
= \(\frac { 1 }{ 2 }\) x PQ x RT
= \(\frac { 1 }{ 2 }\) x 4 x 6 = 2 x 6
= 12 sq. cm

(ii) Area of ∆PQR = 12 sq. cm
⇒ \(\frac { 1 }{ 2 }\) x PR x QS = 12
⇒ \(\frac { 1 }{ 2 }\) x 8 x QS = 12
⇒ QS = \(\frac { 12\times 2 }{ 8 }\)
= 3 cm

Question 5
The base of a triangle 8 cm if height of triangle (RBSESolutions.com) is two times of its base. Then find out the area of triangle.
Solution:
Base of triangle = 8 cm
height of triangle = 2 x 8 = 16 cm

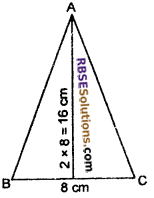
Area of triangle
= \(\frac { 1 }{ 2 }\) x Base x Height
= \(\frac { 1 }{ 2 }\) x 8 x 16
= 4 x 16
= 64 sq. cm

Question 6
ABC is isosceles (RBSESolutions.com) triangle in which AB = AC = 7.6 cm and BC = 9.5 cm (attached fig.) The perpendicular AD from A on side BC is 4 cm. Find area of triangle ABC and measure of perpendicular B BE from B on side AC.

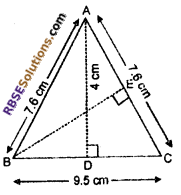
Solution:
In ∆ABC, AB = AC = 7.6 cm
Base BC = 9.5 cm
Height o f triangle AD = 4 cm
Area of ∆ABC = j x Base x Height
= \(\frac { 1 }{ 2 }\) x BC x AD = \(\frac { 1 }{ 2 }\) x 9.5 x 4
= 9.5 x 2 = 19 sq. cm
In isosceles (RBSESolutions.com) triangle ABC
AC = 7.6 cm and BE = ?
Area of ∆ABC = 19 sq. cm
⇒ \(\frac { 1 }{ 2 }\) x AC x BE = 19
⇒ \(\frac { 1 }{ 2 }\) x 7.6 x BE = 19
7.6 x BE = 19 x 2
⇒ BE = \(\frac { 38 }{ 7.6 }\) = 5 cm

Question 7
Ratio of base and height of a parallelogram is 5 : 2. If area is 640 sq. cm then (RBSESolutions.com) find base and height
Solution:
According to figure in parallelogram ABCD, Ratio of base BC and height AE is 5 : 2.
Let base of parallelogram = 5x
Height of parallelogram = 2x
Area of parallelogram = 640

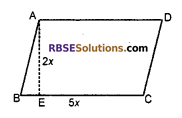
⇒ Base x Height = 640
⇒ 5x × 2x = 640
⇒ 10x² = 640
⇒ x² = \(\frac { 640 }{ 10 }\)
⇒ x² = 64 ⇒x = 8
Base of parallelogram = 5x = 5 x 8 = 40 cm
Height of parallelogram = 2x = 2×8=16cm

Question 8
Shyaivi has a rectangular garden of length 95 metre and breadth 80 metre. He (RBSESolutions.com) wants to plant trees by digging 5 metre broad area outside the garden. Find out the area in which he will plant trees.
Solution:
Length of rectangular garden = 95 m
and breadth = 80 m
After digging 5 m wide around it now garden will be PQRS.

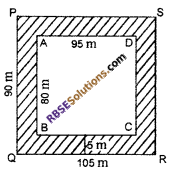
Length =95 + 5 + 5 = 105 m
Breadth= 80 + 5 + 5
= 90 m
Area of rectanglular (RBSESolutions.com) garden = Length x Breadth
= 95 x 80 = 7600 sq. m
Area of rectangle PQRS with plantation = Length x Breadth
= 105 x 90 = 9450 sq. m
Area of plantation part
= Area of PQRS – Area of ABCD
= 9450 – 7600
= 1850 sq.m

Question 9
A 2 metre wide path is present to the inner side of (RBSESolutions.com) a square ground of side 60 metre. Find out :
(1) Area of path
(2) Expenditure on cementing the path at the rate of ₹270 per square metre.
Solution:
Side of square shape field = 60m
Area of PQRS = (side)²
= 60² = 60 x 60 = 3600 sq. m

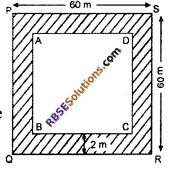
Inside the field 2 m wide path is available.
Therefore a square shape field will be inside (RBSESolutions.com) the field, side of square ABCD = (60 – 2 – 2) = 60 – 4 = 56 m
Area of ABCD = 56²
= 56 x 56 = 3136 sq. m
(1) Area of path
= Area of PQRS – area of ABCD
= 3600-3136 = 464 sq.m
(2) Expenditure on 1 square meter cementing
= ₹270
Expenditure of cementing on 464 sq. m
= 464 x 270
= ₹1,25,280

Question 10
Two pathways parallel to the length and breadth have (RBSESolutions.com) been constructed in the Centre of a rectangular park. Whose length is 125 m. and breadth is 95 m. If width of each parthway is 10 metre. Find out:
(i) expenditure on putting soil on the pathway at the rate of ? 80 per square meter.
(ii) area of putting grass excluding the paths.
Solution:
(1) Let A BCD and EFGH are perpendicular path

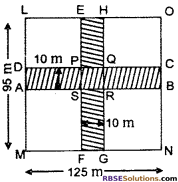
AB = 125 m
BC = 10 m
∴ Area of ABCD
= 125 x 10
= 1250 sq. m
∴ Again EF = 95 m
and FG = 10 m
∴ Area of EFGH = 95 x 10
= 950 sq. m
PQRS is common area (RBSESolutions.com) in both the paths
∴ Area of PQRS = 10 x 10 = 100 sq. m
Area of both paths = Area of ABCD + Area of EFGH – Area of PQRS
= (1250 + 950 – 100) = (2200 – 100)
= 2100 sq. m
Expenditure on putting soil on 1 m² = ₹80
Expenditure on putting soil on 2100 sq. m = 2100 x 80 = ₹1,68,000

(2) Area of rectangular park
= 125 x 95 = 11875 sq. m
Area of putting grass = Area of LMNO – Area of both paths
= 11875 – 2100 = 9775 sq. m

We hope the RBSE Solutions for Class 7 Maths Chapter 16 Perimeter and Area Ex 16.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 7 Maths Chapter 16 Perimeter and Area Exercise 16.2, drop a comment below and we will get back to you at the earliest.