RBSE Solutions for Class 8 Maths Chapter 1 Rational Numbers Additional Questions is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 1 Rational Numbers Additional Questions.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Rational Numbers |
| Exercise | Additional Questions |
| Number of Questions | 41 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 8 Maths Chapter 1 Rational Numbers Additional Questions
I. Objective Type Questions
Question 1.
Rational numbers are closed for –
(a) addition and multiplication
(b) addition and(RBSESolutions.com) subtraction
(c) addition, subtraction and multiplication
(d) none of these
Question 2.
Rational numbers are not associative for –
(a) addition
(b) multiplication
(c) both (a) and (b)
(d) division
Question 3.
Additive inverse of \(\frac { a }{ b }\) is –
(a) \(\frac { a }{ b }\)
(b) \(-\frac { a }{ b }\)
(c) \(\frac { b }{ a }\)
(d) a × b
![]()
Question 4.
Which property of multiplication is illustrated by –
![]()
(a) Commutative
(b) Inverse
(c) Associative
(d) None of these
Question 5.
What is the multiplicative inverse of \(\frac { 8 }{ 21 }\) ?
(a) \(-\frac { 8 }{ 21 }\)
(b) 1
(c) 0
(d) \(\frac { 21 }{ 8 }\)
Question 6.
Give one rational number between \(\frac { 1 }{ 4 }\) and \(\frac { 1 }{ 2 }\)
(a) \(\frac { 3 }{ 4 }\)
(b) 1
(c) \(\frac { 3 }{ 8 }\)
(d) \(\frac { 1 }{ 8 }\)
![]()
Question 7.
Rational number(RBSESolutions.com)between two rational numbers are –
(a) one
(b) four
(c) infinite
(d) zero
Question 8.
Multiplicative inverse of \(3\frac { 1 }{ 3 }\) is –
(a) 3
(b) \(-\frac { 1 }{ 3 }\)
(c) 0.3
(d) None of these
Question 9.
a x b = b x a follows which property?
(a) Associative
(b) Closed
(c) Inverse
(d) Commutative
![]()
Question 10.
a x (b x c) = (a x b) x c follows which property?
(a) Associative under multiplication
(b) Commutative under multiplication
(c) Associative(RBSESolutions.com)under Addition
(d) Commutative under Addition
Question 11.
Additive inverse of rational number \(-\frac { 3 }{ 5 }\) is
(a) 0
(b) 1
(c) \(\frac { 3 }{ 5 }\)
(d) \(-\frac { 5 }{ 3 }\)
Answers
1. (c)
2. (d)
3. (b)
4. (a)
5. (d)
6. (c)
7. (c)
8. (c)
9. (d)
10. (a)
11. (c).
![]()
II. Fill in the blanks
Question 1.
Rational numbers are____under subtraction.
Question 2.
The rational number___is the additive identity for rational numbers.
Question 3
\(\frac { 3 }{ 8 } \times \_ \_ =1\times \frac { 3 }{ 8 } =\frac { 3 }{ 8 } \)
Question 4
___can be represented on a number line.
Question 5.
Between any two(RBSESolutions.com)rational numbers there are ___ rational numbers.
Answers.
1. closed
2. zero
3. 1
4. rational numbers
5. infinite.
![]()
III. True/False Type Questions
Question 1.
Multiplicative Identity of \(-1\frac { 1 }{ 8 }\) is \(\frac { 8 }{ 9 }\).
Question 2.
Additive Inverse of \(\frac { -7 }{ 19 }\) is \(\frac { 7 }{ 19 }\)
Question 3.
Rational numbers are(RBSESolutions.com)represented on number line.
![]()
Question 4.
\(\left( \frac { a+b }{ 2 } \right) \) is the rational number between two rational numbers a and b.
Question 5.
Every natural number is a rational number.
Answers
1. False
2. True
3. True
4. True
5. True.
IV. Matching Type Questions
Match Section A to section B.
| Section A | Section B |
| 1. Rational number between 0 and 1 | (a) – 1 |
| 2. Additive inverse of rational number 1 | (b) undefined |
| 3. Multiplicative inverse of rational number 0 | (c) infinite |
| 4. How many rational number between two rational number | (d) \(\frac { 1 }{ 2 }\) |
Answers
1. (d)
2. (a)
3. (b)
4. (c)
![]()
V. Very Short Answer Type Questions
Question 1.
Define rational numbers.
Solution.
Rational number is(RBSESolutions.com)the quotient of two integers such that the denominator is a non-zero inter, i.e. Rational number = \(\frac { p }{ q }\), where p and q are integers and q ≠ 0
Question 2.
What is the multiplicative identity for rational numbers?
Solution.
1
Question 3.
Find \(\frac { -2 }{ 3 } \times \frac { 4 }{ 5 } \)
Solution.
\(\left( \frac { -2 }{ 3 } \right) \times \left( \frac { 4 }{ 5 } \right) =\frac { -8 }{ 15 } \)
Question 4.
Write the additive inverse of \(-\frac { 7 }{ 19 }\) and varify.
Solution.
\(-\frac { 7 }{ 19 }\) is the additive inverse of \(-\frac { 7 }{ 19 }\).
Verification:
![]()
Question 5.
Find the mean of \(\frac { 3 }{ 8 }\) and \(\frac { 1 }{ 2 }\)
Solution.
![]()
Question 6.
Is 0.6 is multiplicative inverse of \(1\frac { 2 }{ 3 }\)? Why or why not?
Solution.
Yes, 0.6 is multiplicative(RBSESolutions.com)of \(1\frac { 2 }{ 3 }\)
Because
![]()
![]()
VI. Short Answer Type Questions
Question 1.
Subtract a Rational number \(\frac { -3 }{ 8 }\) from \(\frac { -5 }{ 4 }\)
Solution.
\(\frac { -5 }{ 4 } -\left( \frac { -3 }{ 8 } \right) \)
We find out the LCM of denominator 4 and 8. LCM of 4 and 8 is 8
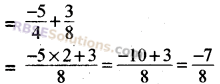
Question 2.
Find ten rational(RBSESolutions.com)number between \(\frac { -5 }{ 6 }\) and \(\frac { 5 }{ 8 }\).
Solution.
LCM of 6 and 8 is 24
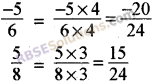
So we can write ten rational number between \(\frac { -5 }{ 6 }\) and \(\frac { 5 }{ 8 }\) are
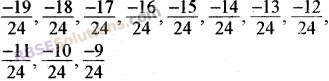
![]()
Question 3.
Find the value of
![]()
Solution.
LCM of 7, 11, 21, 22 = 462
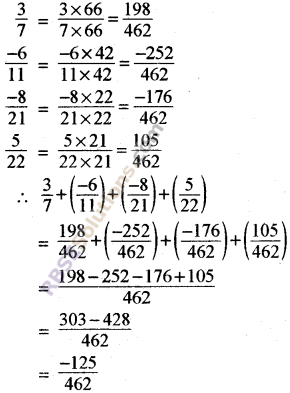
Question 4.
Product of two(RBSESolutions.com)rational number is \(\frac { -28 }{ 81 }\). If one rational number is \(\frac { 14 }{ 27 }\) then find the other
Solution.
According to question,
\(\frac { 14 }{ 27 }\) x IInd number = \(\frac { -28 }{ 81 }\)
⇒ IInd number is
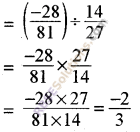
Hence, II nd number is \(\frac { -2 }{ 3 }\)
![]()
Question 5.
Find the value of
(x + y) ÷ (x – y)
If x = \(\frac { 5 }{ 4 }\), y = \(-\frac { 1 }{ 3 }\)
Solution
x + y = \(\frac { 5 }{ 4 } +\left( -\frac { 1 }{ 3 } \right) \)
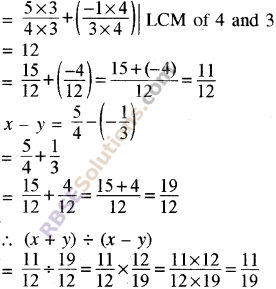
![]()
Question 6.
By what number should we multiply \(\frac { 3 }{ -14 }\),so that the product may be \(\frac { 5 }{ 12 }\).
Solution
We have
Product of(RBSESolutions.com)two numbers = \(\frac { 5 }{ 12 }\)
One number is \(\frac { 3 }{ -14 }\)
∴ The other number = \(\frac { 5 }{ 12 } \div \frac { 3 }{ \left( -14 \right) } \)
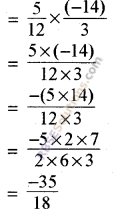
![]()
Question 7.
Subtract the sum of \(\frac { 5 }{ 14 }\) and \(\frac { -4 }{ 7 }\) from the sum of \(\frac { 9 }{ 14 }\) and \(\frac { 23 }{ 14 }\)
Solution.
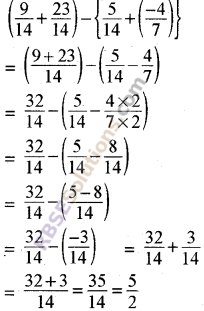
![]()
Question 8.
![]()
Solution.
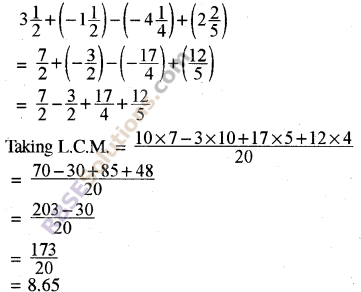
We hope the given RBSE Solutions for Class 8 Maths Chapter 1 Rational Numbers Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 1 Rational Numbers Additional Questions, drop a comment below and we will get back to you at the earliest.