RBSE Solutions for Class 8 Maths Chapter 14 क्षेत्रफल In Text Exercise is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 14 क्षेत्रफल In Text Exercise.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 14 |
| Chapter Name | क्षेत्रफल |
| Exercise | In Text Exercise |
| Number of Questions | 2 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 8 Maths Chapter 14 क्षेत्रफल In Text Exercise
पृष्ठ 168
करो और सीखो
प्रश्न 1
अजहर के पास समलम्ब चतुर्भुज के आकार का एक खेत है (चित्रानुसार)। वह इसे तीन अलग-अलग भागों में बाँटकर देखता है। यदि खेत के विभिन्न भागों की माप चित्रानुसार दी गई हो तो प्रत्येक भाग का(RBSESolutions.com) क्षेत्रफल ज्ञात कर दर्शाइए कि समलम्ब चतुर्भुज PQRS का क्षेत्रफल = ∆SPT का क्षेत्रफल + आयत STUR का क्षेत्रफल + ∆RUQ का क्षेत्रफल होता है। एवं समलम्ब चतुर्भुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\)(a+ b) xh में मान रख तुलना कीजिए।
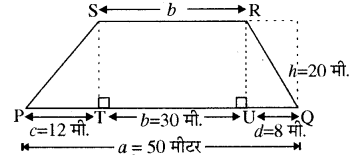
हल:
∆ SPT का क्षेत्रफल

आयत STUR का क्षेत्रफल
= लम्बाई x चौड़ाई
= TU x TS
= 30 x 20
= 600 मी2
∆ RUQ का क्षेत्रफल

∴ समलम्ब चतुर्भुज PQRS का क्षेत्रफल = ∆ SPT का क्षेत्रफल + आयत STUR
का क्षेत्रफल + ∆ RUQ का क्षेत्रफल
= 120 मी.2 + 600 मी.2 + 80 मी.2
= 800 मी.2 …..(1)
पुनः, समलम्ब(RBSESolutions.com) चतुर्भुज PQRS का क्षेत्रफल
= \(\frac { 1 }{ 2 }\)(a + b) x h
= \(\frac { 1 }{ 2 }\) [50 + 30] x 20
= 800 मी.2 ………..(2)
(1) व (2) से हम पाते हैं कि दोनों प्रकार से प्राप्त समलम्ब चतुर्भुज PQRS का क्षेत्रफल समान ही आता है।
![]()
पृष्ठ 169
करो और सीखो
प्रश्न 2
क्या विभिन्न परिमापों वाले समलम्ब चतुर्भुज, क्षेत्रफल में समान होते हैं? दी गई मापों को देखकर तथ्य को स्थापित कीजिए।
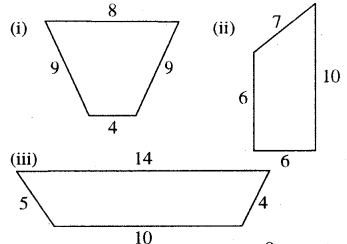
हल:
(i) समलम्ब चतुर्भुज
ABCD का परिमाप = 4 + 9 + 8 + 9 = 30 इकाई
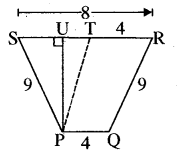
QR तथा PT समान्तर हैं तथा
PU ⊥ RS
∵ PT ॥ QR तथा PQ॥ TR
∴ PQRT एक(RBSESolutions.com) समान्तर चतुर्भुज है।
∴ PT = QR = 9 इकाई तथा TR = PQ= 4 इकाई
∴ ST = RS – RT = 8 – 4 = 4 इकाई

= 2\(\sqrt { 77 }\) = 17.54 वर्ग इकाई
पुनः ∆PTS का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x ST x PU
⇒ 17.54 = \(\frac { 1 }{ 2 }\) x 4 x PU = 2 PU
⇒ PU = \(\frac { 17.54 }{ 2 }\) = 8.77 इकाई
अत: समलम्ब(RBSESolutions.com) चतुर्भुज PQRS का क्षेत्रफल
= \(\frac { 1 }{ 2 }\) x (PQ+ RS) x PU
= \(\frac { 1 }{ 2 }\) x (4 + 8) x 8.77
= 6 x 8.77 = 52.62 वर्ग इकाई
![]()
(ii) समलम्ब चतुर्भुज (ii) का क्षेत्रफल
= \(\frac { 1 }{ 2 }\) x (समान्तर भुजाओं का योग) x ऊँचाई
= \(\frac { 1 }{ 2 }\) x (6 + 10) x 6
= 48 वर्ग इकाई
(iii) समलम्ब चतुर्भुज P’Q’R’S’ का परिमाप = 10 + 4 + 14 + 5 = 33 इकाई
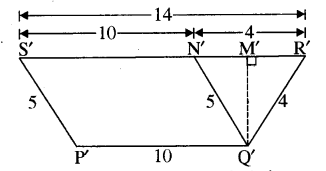
Q’N’ ॥ S’P’ तथा Q’M’ ⊥ S’R’ खींचते हैं।
Q’N’ ॥ S’P’ 7911 P’Q’ ॥ S’R’ ⇒ P’Q’ ॥ S’N’
∴ P’Q’N’S’ एक(RBSESolutions.com) समान्तर चतुर्भुज है।
Q’N’ = P’S’ =5 इकाई तथा S’N’ = P’Q’ = 10 इकाई
R’N’ = S’R’ – S’N’ = 14 – 10 = 4 इकाई
∆Q’R’N’ में a = 4, b = 5, c = 4
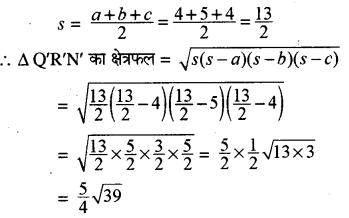
= \(\frac { 5 }{ 4 }\) x 6.24 = 7.80वर्ग इकाई
पुनः ∆Q’R’N’ का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x N’R’ x Q’M’
⇒ 7.80 = \(\frac { 1 }{ 2 }\) x 4 x Q’M’ = 2Q’M’
⇒ Q’M’ = \(\frac { 7.80 }{ 2 }\) = 3.9 इकाई
समलम्ब(RBSESolutions.com) चतुर्भुज P’Q’R’S’ का क्षेत्रफल
= \(\frac { 1 }{ 2 }\) (P’Q’+ R’S’) x Q’M’
= \(\frac { 1 }{ 2 }\) (10 + 14) x 3.9
= 12 x 3.9 = 46.8 वर्ग इकाई
(i), (ii) व (iii) से हम इस तथ्य पर पहुँचते हैं कि विभिन्न परिमापों वाले समलम्ब चतुर्भुज, क्षेत्रफल में समान नहीं होते हैं।
![]()
We hope the RBSE Solutions for Class 8 Maths Chapter 14 क्षेत्रफल In Text Exercise will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 14 क्षेत्रफल In Text Exercise, drop a comment below and we will get back to you at the earliest.