RBSE Solutions for Class 8 Maths Chapter 6 Polygons Ex 6.1 is part of RBSE Solutions for Class 8 Maths. Here we have given Rajasthan Board RBSE Class 8 Maths Chapter 6 Polygons Exercise 6.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Chapter Name | Polygons |
| Exercise | Exercise 6.1 |
| Number of Questions | 12 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 8 Maths Chapter 6 Polygons Ex 6.1
Question 1.
Draw the diagonal with the help of a pencil in the following figure and tell
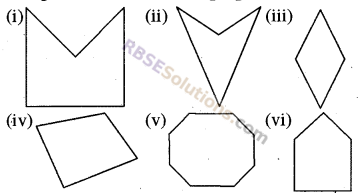
(i) In which shapes, diagonal will be inside?
(ii) In which shapes, diagonal(RBSESolutions.com)will be outside?
(iii) Identify the type of polygon (Concave or Convex)?
Solution
(i)
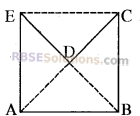
diagonals : AC,AD,BD,BE,CE
(ii)
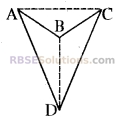
diagonals : AC,BD
(iii)
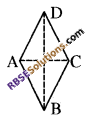
diagonals : AC,BD
![]()
(iv)
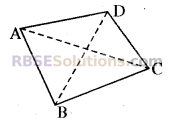
diagonals : AC,BD
(v)
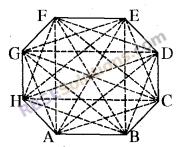
diagonals : AC, AD, AE, AF, AG, BD, BE, BF, BG, BH, CE, CF, CG, CH, DF, DG, DH, EG, EH, FH
(vi)
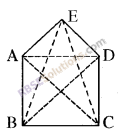
diagonals : AC, AD, BD, BE, CE
(i) Diagonals are inside in the figures (iii), (iv) , (v) and (vi)
(ii) Diagonals are outside(RBSESolutions.com)in figures (i) and (ii)
(iii) Types of figures (i) Concave (ii) Concave (iii) Convex (iv) Convex (v) Convex (vi) Convex.
![]()
Question 2.
In the given polygon ABCDE,
(i) Write name of interior angles.
(ii) Write name of exterior angles.
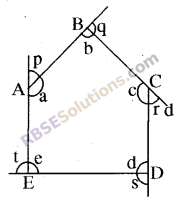
Solution
(i) Interior angles are— a, b, c, d, e
(ii) Exterior angles are— p, q, r, s, t
Question 3.
Define the regular polygon. Identify that regular polygon in which there are :
(i) 5 sides
(ii) 6 sides
(iii) 8 sides.
Solution
Regular polygon—A closed figure of three or more than three equal sides is called regular polygon.
(i) Closed figure of 5 sides : pentagon.
(ii) Closed figure of 6 sides : hexagon.
(iii) Closed(RBSESolutions.com)figure of 8 sides : Octagon.
![]()
Question 4.
Find the value of unknown angles (w, x, y, z) in the following figures.
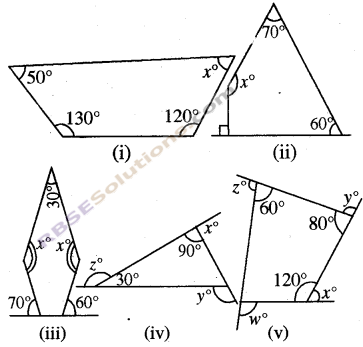
Solution
(i) ∵ Sum of all internal angles of a quadrilateral is 360°, therefore,
x + 120° + 130° + 50° = 360°
⇒ x+ 300° = 360°
⇒ x = 360° – 300° = 60°
(ii) ∵ Sum of all internal angles of a quadrilateral is 360°, therefore
x + 90° + 60° + 70° = 360°
⇒ x + 220° = 360°
⇒ x = 360° – 220° = 140°
![]()
(iii) ∵ Sum of all internal angles of a Pentagon = (5 – 2) 180° therefore,
30° + x + (180° – 70°) + (180° – 60°) + x = 540°
⇒ 30° + x + 110° + 120° + x = 540°
⇒ 2x + 260° = 540°
⇒ 2x = 540° – 260°
⇒ 2x = 280°
\(x=\frac { 280 }{ 2 }\)
⇒ x = 140°
(iv) ∵ Sum of angles(RBSESolutions.com)of a triangle is 180°, so
90° + 30° + (180° – y)= 180°
⇒ 300° – y = 180°
⇒ y = 300° – 180°
⇒ y = 120°; x + 90° = 180°
⇒ x = 180° – 90° = 90°;
z + 30° = 180°
z = 180° -30° = 150°
(v) x + 120° = 180°
⇒ x = 180° – 120° = 60°
y + 80° = 180°
⇒ y = 180° – 80° = 100°
z + 60° = 180°
⇒ z = 180° – 60° = 120°
∵ Sum of all internal angles of a – quadrilateral is 360° therefore,
180° – w + 120° + 80° + 60° = 360°
⇒ 440° – w = 360°
⇒ w = 440° – 360° = 80°
Question 5.
Find the number of sides of a regular polygon whose measure of each exterior angle is 45°
Solution
Let the number of sides be n
Sum of all exterior angle of n side regular polygon = 360°
∴ each exterior(RBSESolutions.com)angle = \(\frac { { 360 }^{ o } }{ n } \)
According to question 45° = \(\frac { { 360 }^{ o } }{ n } \)
⇒ 45 °n = 360°
⇒ \(n=\frac { { 360 }^{ o } }{ { 45 }^{ o } } =8\)
n = 8
Number of sides = 8
![]()
Question 6.
Find the number of sides of a regular polygon if its each interior angle is 165°.
Solution
Each interior angle = 165°
∴ Each exterior angle = 180° – 165° = 15°
Let the number of sides be n.
Sum of all exterior angles of polygon = 360°
∴ Value of each(RBSESolutions.com)angle = \(\frac { { 360 }^{ o } }{ n } \)
According to question \(\frac { { 360 }^{ o } }{ n } \) = 15°
⇒\(n=\frac { { 360 }^{ o } }{ { 15 }^{ o } } =24\)
Therefore, the number of sides be 24
![]()
Question 7.
Find the number of sides of that regular polygon whose each exterior angle is 24°.
Solution
Let the number of sides be n.
Sum of all exterior angles of a polygon = 360°
Each angle of(RBSESolutions.com)exterior = \(\frac { { 360 }^{ o } }{ n } \)
According to question \(\frac { { 360 }^{ o } }{ n } \) = 24°
⇒\(n=\frac { { 360 }^{ o } }{ { 24 }^{ o } } \)
⇒ n = 15
Therefore, number of sides = 15.
Question 8.
Find the value of every interior angle of that regular polygon which has 10 sides.
Solution
Here n = 10
Value of each internal angle of n sided
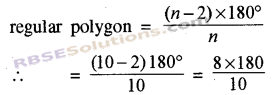
= 144°
Therefore, the value of each interior angle of a regular polygon = 144°.
![]()
Question 9.
If interior angles of any polygon is 115° then will it be regular polygon?
Solution
Measure of each interior angle of n sided

which is not a natural number.
Since, number of sides of polygon is not a whole number.
∴ Such regular(RBSESolutions.com)polygon is not possible.
![]()
Question 10.
One interior angle of a hexagon is 165° and the measure of remaining interior angle is x° then find out the measure of all the angles.
Solution
Sum of interior angles of a hexagon
= (n – 2) x 180°
= (6 – 2) x 180°
= 4 x 180° = 720°
According to question,
⇒ 165° + x° + x° + x° + x° + x° = 720°
⇒ 165° + 5x° = 720°
⇒ 5x° = 720° – 165°
⇒ 5x° = 555°
⇒ 5x = 555
⇒ \(x=\frac { 555 }{ 5 }\)
⇒ x = 111
![]()
Question 11.
By increasing the sides of a triangle in a single direction, obtained exterior angles are 110°, 115° and x°, then find the value of x.
Solution
We know sum of all exterior angles of a regular polygon = 360°
⇒ 110° + 115° + x° = 360°
⇒ 225° + x° = 360°
⇒ x° = 360° – 225°
⇒ x° = 135°
Question 12.
Find the sum of all interior angles of a regular heptagon.
Solution
Here n = 7
∴ Sum of all interior(RBSESolutions.com)angles of a regular polygon
= (n – 2) 180°
= (7 – 2) 180°
= 5 x 180°
= 900°
![]()
We hope the given RBSE Solutions for Class 8 Maths Chapter 6 Polygons Ex 6.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 8 Maths Chapter 6 Polygons Exercise 6.1, drop a comment below and we will get back to you at the earliest.