RBSE Solutions for Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Miscellaneous Exercise is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Miscellaneous Exercise.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Chapter Name | सरल रेखीय आकृतियाँ |
| Exercise | Miscellaneous Exercise |
| Number of Questions Solved | 32 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Miscellaneous Exercise
विविध प्रश्नमाला
प्रश्न 1.
यदि किसी त्रिभुज में दो कोण 90° एवं 30° माप के हो, तो तीसरा कोण है।
(A) 90°
(B) 30°
(C) 60°
(D) 120°
उत्तर : (C)
संकेत : त्रिभुज के लिए, माना तीसरा कोण है, तो
90° + 30° + x = 180°
या x = 180° – (90° + 30°) = 180° – 120° = 60°
प्रश्न 2.
एक त्रिभुज के तीनों कोणों के(RBSESolutions.com)मापों का अनुपात 2 : 3 : 4 है, तो उसके सबसे बड़े कोण का माप है।
(A) 80°
(B) 60°
(C) 40°
(D) 180°
उत्तर : (A)
संकेत : माना कि त्रिभुज के तीन कोण 2x, 3x तथा 4x है,
तो 2x + 3x + 4x = 180°
⇒ 9x = 180°
⇒ x = 20°
सबसे बड़ा कोण = 4x = 4 × 20° = 80°
![]()
प्रश्न 3.
एक समबाहु त्रिभुज के प्रत्येक कोण की मापं है:
(A) 90°
(B) 30°
(C) 45°
(D) 60°
उत्तर : (D)
प्रश्न 4.
एक चतुर्भुज के चारों कोणों की माप का अनुपात 1 : 2 : 3 : 4 है तो उसके सबसे छोटे कोण की माप है:
(A) 120°
(B) 36°
(C) 18°
(D) 10°
उत्तर : (B)
संकेत : माना त्रिभुज के कोण x, 2x, 3x तथा 4 हैं।
तब x + 2x + 3x + 4x = 360°
⇒ 10x = 360°
⇒ x = 36°
अत: सबसे छोटा कोण = x = 36°
![]()
प्रश्न 5.
चित्र में, ∆ABC की भुजा BC को बिन्दु D तक बढ़ाया(RBSESolutions.com)गया है। यदि ∠A = 55° और। ∠B = 60° हो तो ∠ACD की माप है:
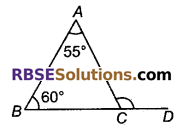
(A) 120°
(B) 110°
(C) 115°
(D) 125°
उत्तर : (C)
संकेत : ∠ACD = ∠B + ∠A = 60° + 55° = 115°
प्रश्न 6.
एक षट्भुज के सभी अन्तः कोणों को योग है:
(A) 720°
(B) 360°
(C) 540°
(D) 1080°
उत्तर : (C)
संकेत : षट्भुज के लिए, n = 6
अन्तः कोणों का योग = (n – 2) x 180°
= (6 – 2) x 180°
= 4 × 180°
= 720°
![]()
प्रश्न 7.
एक n भुजा वाले बहुभुज की भुजाओं को एक ही क्रम में बढ़ाने से बने बहिष्कोणों का योग है।
(A) n समकोण
(B) 2n समकोण
(C) (2n – 4) समकोण
(D) 4 समकोण
उत्तर : (D)
प्रश्न 8.
एक समबहुभुज में भुजाओं की संख्या n है तो उसके प्रत्येक अन्तः कोण की माप हैः
(A) \(\frac { 360 }{ n }\) अंश
(B) (\(\frac { 2n-4 }{ n }\)) समकोण
(C) n समकोण
(D) 2n समकोण
उत्तर : (B)
प्रश्न 9.
यदि किसी त्रिभुज का एक कोण अन्य दो कोणों के योग के बराबर से, तो वह त्रिभुज है एक:
(A) समद्विबाहु त्रिभुज
(B) अधिककोण त्रिभुज
(C) समबाहु(RBSESolutions.com)त्रिभुज
(D) समकोण त्रिभुज
उत्तर : (D)
संकेत : माना त्रिभुज के कोण = x°, y°, z° है।
तो प्रश्नानुसार, y° = x + z° (माना) ….(i)
तथा x° + y° + z° = 180° …(ii)
समी. (i) व (ii) से,
y° + y° = 180°
⇒ y° = 90°
अत: यह त्रिभुज समकोण त्रिभुज है।
![]()
प्रश्न 10.
एक त्रिभुज का एक बहिष्कोण 105° है तथा उसके दोनों(RBSESolutions.com)अन्तराभिमुख कोण बराबर हैं। इनमें से प्रत्येक बराबर कोण है:
(A) 37\(\frac { 1 }{ 2 }\)
(B) 52\(\frac { 1 }{ 2 }\)
(C) 72\(\frac { 1 }{ 2 }\)
(D) 75°
उत्तर : (B)
संकेत : माना अन्तराभिमुख कोण x है तो
x + x = 105°
⇒ 2x = 105°
⇒ x = 52\(\frac { 1 }{ 2 }\)
प्रश्न 11.
किसी त्रिभुज के कोणों का अनुपात 5 : 3 : 7 है। वह त्रिभुज है एक:
(A) न्यूनकोण त्रिभुज
(B) अधिककोण त्रिभुज
(C) समकोण(RBSESolutions.com)त्रिभुज
(D) समद्विबाहु त्रिभुज
उत्तर : (A)
संकेत : दिया है, कोणों का अनुपात = 5 : 3 : 7
माना कि त्रिभुज के तीनों कोण 5x, 3x तथा 7x हैं।
5x + 3x + 7x = 180°
⇒ 15x = 180°
⇒ x = 12
अतः तीनों कोण 5 × 12, 3 × 12, 7 × 12
= 60°, 36°, 84°
= न्यूनकोण त्रिभुज
![]()
प्रश्न 12.
यदि किसी त्रिभुज का एक कोण 130° है, तो अन्य दोनों कोणों के समद्विभाजकों के बीच का कोण हो सकता है।
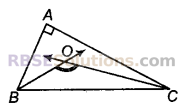
(A) 50°
(B) 65°
(C) 145°
(D) 155°
उत्तर : (D)
संकेत : ∠BOC = 90°+ \(\frac { 1 }{ 2 }\) ∠A
अतः दोनों कोणों के समद्विभाजकों(RBSESolutions.com)के बीच कोण = 90° + \(\frac { 1 }{ 2 }\) × 130° = 90° + 65° = 155°
प्रश्न 13.
चित्र में, ∠A की माप बताइए।
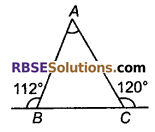
हल
∠ABC = 180° – 112° = 68°
∠ACB = 180° – 120° = 60
∆ABC में,
∠A + ∠ABC + ∠ACB = 180°
⇒ ∠A + 68° + 60° = 180°
⇒ ∠A + 128° = 180°
⇒ ∠A = 180° – 128° = 52°
![]()
प्रश्न 14.
चित्र में, ∠B = 60° और ∠C = 40° है। ∠A का माप बताइए।
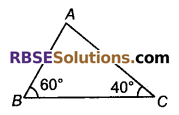
हुल
∆ABC में,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 60° + 40° = 180°
⇒ ∠A + 100° = 180°
⇒ ∠A = 180° – 100° = 80°
प्रश्न 15.
चित्र में m || QR, तो ∠QPR का माप बताइए।
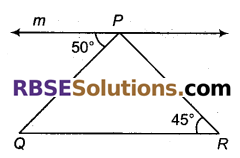
हल
दिया है m || QR, माना बिन्दु S रेखा m पर है।

∠QRP = ∠RPS = 45° (एकान्तर कोण)
अतः ∠QPR + 50° + 45° = 180°
⇒ ∠QPR + 95° = 180°
⇒ ∠QPR = 180° – 95° = 85°
![]()
प्रश्न 16.
दिए गए चित्र में ∠A का माप बताइए।
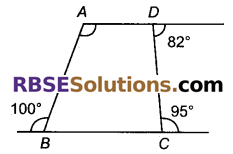
हल
∠ABC = 180° – 100° = 80°
∠DCB = 180° – 95° = 85°
∠CDA = 180° – 82° = 98°
चतुर्भुज के चारों अन्त:कोणों का योग = 360°
⇒ ∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
⇒ 80° + 85° + 98° + ∠DAB = 360°
⇒ 263° + ∠DAB = 360°
⇒ ∠DAB = 360° – 263° = 97°
प्रश्न 17.
एक पंचभुज के चार अन्तः कोण 40°, 75°, 125° और 135° है तो पाँचवें कोण की माप बताइए।
हल
पंचभुज के पाँचों अन्तः कोणों का योग = (2n – 4) समकोण
40° + 75° + 125° + 135° + x = (2 × 5 – 4) × 90° (माना x पाँचवाँ कोण, n = 5)
⇒ 375° + x = 540°
⇒ x = 540° – 375° = 165°
अत: पाँचवाँ कोण 165° है।
![]()
प्रश्न 18.
एक समबहुभुज का प्रत्येक बहिष्कोण 45° है तो उसकी भुजाओं की संख्या बताइए।
हल

प्रश्न 19.
एक समबहुमुक्लीनं भुजाओं की संख्या 12 है तो उसके प्रत्येक अन्त: कोण की माप बताइए।
हल

![]()
प्रश्न 20.
एक बहुभुज के सभी अन्तः कोणों का योगफल 10 समकोण है तो भुजाओं की संख्या बताइए।
हल
बहुभुज के अन्तः कोणों का योग = (n – 2) × 180°
10 समकोण = (n – 2) × 180°
⇒ 10 × 90°= (n – 2) × 180°
⇒ (n – 2) = 5
⇒ n = 7
अतः भुजाओं की संख्या 7 है।
प्रश्न 21.
क्या 110° माप के प्रत्येक अन्त: कोण का कोई एक बहुभुज हो सकता है? जाँच कीजिए।
हल
दिए गए बहुभुज का प्रत्येक कोण = 110°
प्रत्येक बहिष्कोण = 180° – 110° = 70°
अब माना भुजाओं की संख्या n है।
एक बहुभुज के सभी(RBSESolutions.com)बहिष्कोणों का योग = 4 समकोण
बहिष्कोणों का योग = 4 समकोण
n × 70° = 360°
⇒ n = 5.14, जोकि एक पूर्ण संख्या नहीं है।
अतः 110° माप के प्रत्येक अन्तः कोण वाला एक बहुभुज नहीं हो सकता।
![]()
प्रश्न 22.
यदि एक ΔABC में ∠A + ∠B = ∠C हो, तो ΔABC का सबसे बड़ा कोण ज्ञात कीजिए।
हल
∠A + ∠B = ∠C
अत: कोण C सबसे बड़ा कोण है।
प्रश्न 23.
एक अष्टभुज के सभी अन्त:कोणों का योगफल ज्ञात कीजिए।
हल
दिया है, n = 8 तब सभी अंन्त: कोणों का योग
= (n – 2) × 180°
= (8 – 2) × 180°
= 6 × 180° = 1080°
प्रश्न 24.
एक समदशभुज के प्रत्येक अन्त: कोण की माप ज्ञात कीजिए।
हल
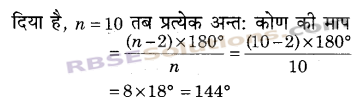
![]()
प्रश्न 25.
एक त्रिभुज की भुजाओं को एक ही क्रम में बढ़ाने से प्राप्त बहिष्कोण क्रमशः 110°, 130° एवं x° है, तो x° का मान ज्ञात कीजिए।
हल
सभी बहुभुजों में प्राप्त बक्षिसों का योग 360° होता है।
अतः 110° + 130° + x° = 360°
⇒ x° = 360° – 240°= 120°
⇒ x° = 120°
![]()
प्रश्न 26.
एक षट्भुज का एक अन्त:कोण 165° है और शेष प्रत्येक अन्त: कोण का माप x° है, तो शेष कोण का माप बताइए।
हल
प्रत्येक अन्त: कोण का मान n भुजा वाले बहुभुज के सभी अन्त: कोणों का योग = (2n – 4) समकोण
5x° + 165° = (2 × 6 – 4) × 90° = 8 × 90° = 720°
x° = 111°
अतः शेष कोण 111° के हैं।
प्रश्न 27.
चित्र में, AB || DC हो तो दिए गए। कोणों से ∠x, ∠y तथा ∠z ज्ञात
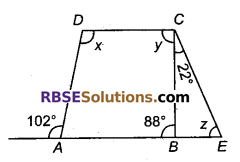
हल
AB|| DC ।
∠x = 102° (एकान्तर कोण)
और 88°= 22° + z
z = 88° – 22° = 66°
(∵ बहिष्कोण = दोनों अन्तराभिमुख अन्त: कोणों(RBSESolutions.com)का योग AB|| DC तथा BC तिर्यक रेखा है।)
88° + y = 180° (एक ही ओर के अन्तः कोणों का योग 180° के बराबर होता है)
y = 180° – 88° = 92°
![]()
प्रश्न 28.
दिए गए चित्र से, ∠x तथा ∠y के माप ज्ञात कीजिए जहाँ ∠x – ∠y = 10° है।
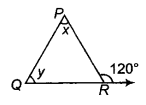
हल
दिया है :
∠x – ∠y = 10° …(i)
∠x + ∠y = 120° ……(ii)
(बहिष्कोण = दोनों अन्तराभिमुख अन्तः कोणों का योगफल)
समीकरण (i) व (ii) को जोड़ने पर
∠x – ∠y + ∠x + ∠y = 10° + 120°
⇒ 2∠x = 130°
⇒ ∠x = 65°
⇒ ∠x + ∠y = 120°
⇒ ∠y = 120° – ∠x = 120° – 65°= 55°
![]()
प्रश्न 29.
एक बहुभुज में दो कोण जिनमें प्रत्येक एक समकोण है और शेष प्रत्येक कोण 150° के बराबर हो तो बहुभुज की भुजाओं की संख्या ज्ञात कीजिए।
हल
माना बहुभुज में दो समकोण के अलावा 150° के n कोण हैं तो इनके बहिष्कोण 30° के होंगे। अतः बहुभुज के बहिष्कोणों का योग
90° + 90° + n × 30° = 180° + n × 30° = 360°
⇒ n × 30° = 360° – 180° = 180°
⇒ n = 6
अत: कुल भुजाएँ = 6 + 2 = 8
प्रश्न 30.
दिए गए चित्र से, सिद् कीजिए कि ∠x + ∠y = ∠A + ∠C
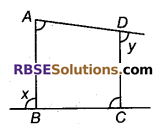
हल
∠ABC + ∠x = 180° (रैखिक कोण युग्म)
⇒ ∠ABC = 180° – ∠x …(i)
इसी प्रकार, ∠CDA + ∠y = 180° (रैखिक कोण युग्म)
∠CDA = 180° – ∠y …(ii)
चतुर्भुज के चारों आन्तरिक(RBSESolutions.com)कोणों का योग (2 × 180°) = 360° होता है।
∠A + ∠C + ∠CDA + ∠ABC = 360°
⇒ ∠A + ∠C + (180° – ∠y) + (180° – ∠x) = 360° (समी (i) व (ii) से)
⇒ ∠A + ∠C + 360° – (∠x + ∠y) = 360°
⇒ ∠A + ∠C = 360° – 360° + ∠x + ∠y = ∠x + ∠y
इति सिद्धम।
![]()
प्रश्न 31.
दिए गए चित्र से, ∠x ज्ञात कीजिए यहाँ रेखाएँ BO एवं CO क्रमश: ∠B एवं ∠C के समद्विभाजक हैं।
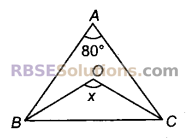
हल
ΔABC के लिए,
∠A + ∠ABC + ∠ACB = 180° (त्रिभुज के तीनों कोणों का योग 180° होता है)
\(\frac { 1 }{ 2 }\) ∠A + \(\frac { 1 }{ 2 }\) ∠ABC + \(\frac { 1 }{ 2 }\) ∠ACB = \(\frac { 180 }{ 2 }\) = 90°
\(\frac { 1 }{ 2 }\) ∠A + ∠OBC + ∠OCB = 90° …(i)
दिया है, BO व CO क्रमशः ∠B व ∠C के समद्विभाजक हैं।
∠BOC + ∠OBC + ∠OCB = 180° …(ii)
समीकरण (ii) में से (i) घटाने पर
∠BOC + ∠OBC + ∠OCB – \(\frac { 1 }{ 2 }\) ∠A – ∠OBC – ∠OCB = 180° – 90° = 90°
⇒ ∠BOC – \(\frac { 1 }{ 2 }\) ∠A = 90°
⇒ ∠BOC = 90° + \(\frac { 1 }{ 2 }\) ∠A
⇒ x = 90° + \(\frac { 1 }{ 2 }\) × 80° = 90° + 40° = 130°
![]()
प्रश्न 32.
चित्र में, ∠Q > ∠R, PA कोण QPR का समद्विभाजक है तथा PM ⊥ QR है। सिद्ध कीजिए। ∠APM = \(\frac { 1 }{ 2 }\) (∠Q – ∠R)
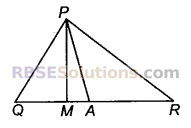
हल
माना ∠1, ∆PMR का बहिष्कोण है।
∠1 = ∠4 + ∠5 + ∠R …..(i)
∠2, ∆PMQ का बहिष्कोण है।
∠2 = ∠3 + ∠Q …(ii)
∠1 = ∠2 = 90° …(iii)
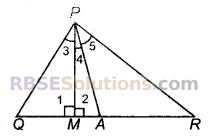
समीकरण (i), (ii) व (iii) से,
∠4 + ∠5 + ∠R = ∠3 + ∠Q
लेकिन ∠5 = ∠4 + ∠3
⇒ ∠4 + ∠3 + ∠4 + ∠R = ∠3 + ∠Q
⇒ 2∠ 4 + ∠R = ∠Q
⇒ 2∠4 = ∠Q – ∠R
⇒ ∠4 = \(\frac { 1 }{ 2 }\) (∠Q – ∠R)
⇒ ∠APM = \(\frac { 1 }{ 2 }\) (∠Q – ∠R)
इति सिद्धम्।
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Miscellaneous Exercise will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 6 सरल रेखीय आकृतियाँ Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.