RBSE Solutions for Class 9 Maths Chapter 9 चतुर्भुज Additional Questions is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Chapter 9 चतुर्भुज Additional Questions.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 9 |
| Chapter Name | चतुर्भुज |
| Exercise | Additional Questions |
| Number of Questions Solved | 19 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 9 Maths Chapter 9 चतुर्भुज Additional Questions
बहुविकल्पीय प्रश्न
प्रश्न 1.
वर्ग की भुजा और विकर्ण का अनुपात है :
(A) 2 : 1
(B) 1 : 2
(C) 1 : 3
(D) 3 : 1
प्रश्न 2.
यदि समान्तर चतुर्भुज की दो संलग्न भुजाएँ समान हैं, तो वह है :
(A) एक आयत
(B) एक वर्ग
(C) एक पतंग
(D) एक समचतुर्भुज
प्रश्न 3.
यदि किसी चतुर्भुज के तीन कोण बराबर हैं, तो वह है, एक :
(A) समान्तर(RBSESolutions.com)चतुर्भुज
(B) समचतुर्भुज
(C) पतंग
(D) कोई नहीं
प्रश्न 4.
यदि चतुर्भुज के विकर्ण परस्पर लम्ब है तो वह है,
(A) समान्तर चतुर्भुज
(B) वर्ग
(C) आयत
(D) पतंग
![]()
प्रश्न 5.
यदि वर्ग के विकर्ण बिन्दु O पर समद्विभाजित होते हैं, तब त्रिभुज AOB है:
(A) एक समद्विबाहु परन्तु समकोण त्रिभुज नहीं
(B) एक समद्विबाहु(RBSESolutions.com)समकोण त्रिभुज
(C) एक समबाहु त्रिभुज
(D) एक समकोण त्रिभुज परन्तु समद्विबाहु नहीं।
प्रश्न 6.
एक चतुर्भुज एक आयत है, परन्तु एक वर्ग नहीं, जब :
(A) इसके विकर्ण समद्विभाजित नहीं होते हैं।
(B) इसके विकर्ण बराबर नहीं हैं।
(C) इसके विकर्ण(RBSESolutions.com)परस्पर लम्ब नहीं हैं।
(D) सभी कोण बराबर नहीं हैं।
प्रश्न 7.
समान्तर चतुर्भुज के किन्हीं दो सलंग्न कोणों के समद्विभाजक प्रतिच्छेद करते हैं:
(A) 90° पर
(B) 80° पर
(C) 45° पर
(D) 100° पर
प्रश्न 8.
यदि समचतुर्भुज का एक विकर्ण उसकी एक भुजा के बराबर है, तब संलग्न कोणों का मान है:
(A) 100°, 80°
(B) 60°, 120°
(C) 90°, 90°
(D) 70°, 110°
![]()
प्रश्न 9.
समलम्ब ABCD की भुजाओं AD और BC के मध्यबिन्दु क्रमश: E और F हैं। यदि AB = x तथा CD = y है, तब, EF बराबर है:
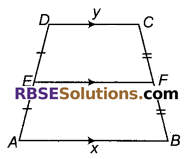
(A) \(\frac { 1 }{ 2 }\) (x + y)
(B) \(\frac { 1 }{ 2 }\) (x – y)
(C) \(\frac { 2xy }{ x+y }\)
(D) \(\frac { x+y }{ 2xy }\)
प्रश्न 10.
संलग्न चित्र में, ABCD एक स्मचतुर्भुज है। (x – y) का मान है:
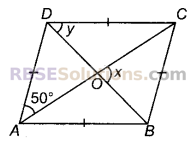
(A) 40°
(B) 60°
(C) 10°
(D) 50°
उत्तरमाला
1. (B)
2. (D)
3. (D)
4. (D)
5. (B)
6. (C)
7. (A)
8. (B)
9. (A)
10. (D)
![]()
अतिलघूय/लघूतटीय प्रश्न
प्रश्न 1.
चित्र में, त्रिभुज ABC की भुजाओं AB, BC तथा AC के मध्य बिन्दु क्रमश: P, Q तथा R हैं। यदि PQ = 2.5 सेमी, QR = 3.0 सेमी तथा PR = 3.5 सेमी हैं, तो ∆ABC का परिमाप ज्ञात करो।
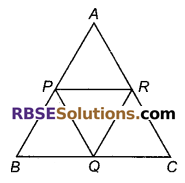
हल:
बिन्दु P तथा ७, भुजाओं AB तथा BC के मध्य बिन्दु हैं।
PQ = \(\frac { 1 }{ 2 }\) AC
⇒ 2.5 = \(\frac { 1 }{ 2 }\) AC
⇒ AC = 5 सेमी
बिन्दु Q तथा R भुजाओं BC तथा AC के मध्य बिन्दु हैं,
QR = \(\frac { 1 }{ 2 }\) AB
⇒ 3.0 = \(\frac { 1 }{ 2 }\) AB
⇒ AB = 6 सेमी
बिन्दु P तथा R भुजाओं AB तथा AC के मध्य बिन्दु हैं।
PR = \(\frac { 1 }{ 2 }\) BC
⇒ 3.5 = \(\frac { 1 }{ 2 }\) BC
⇒ BC = 7 सेमी
∆ABC का परिमाप = AB + BC + AC = 6 + 7 + 5 = 18 सेमी
![]()
प्रश्न 2.
चित्र में, ABC समकोण त्रिभुज है। बिन्दु P तथा Q त्रिभुज की भुजाओं AB तथा AC के मध्य बिन्दु हैं। यदि AB = 10 सेमी। तथा BC = 8 सेमी, तो ∆APQ का क्षेत्रफल ज्ञात करो।
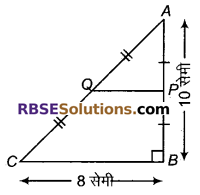
हल:
बिन्दु P तथा Q भुजाओं AB तथा AC के मध्य बिन्दु हैं।
PQ = \(\frac { 1 }{ 2 }\) BC
⇒ PQ = \(\frac { 1 }{ 2 }\) × 8 = 4 सेमी
PQ || BC
अब AP = \(\frac { 1 }{ 2 }\) AB (∵ P, AB का मध्य बिन्दु है)
⇒ AP = \(\frac { 1 }{ 2 }\) × 10 = 5 सेमी
समकोण त्रिभुज का ∠B समकोण है।
∠ABC = 90°
PQ || BC तथा AB एक(RBSESolutions.com)त्रिर्यक रेखा है।
∠APQ = ∠ABC (संगत कोण)
⇒ ∠APQ = 90°
अतः त्रिभुज APQ कोण P पर समकोण है। समकोण ∆APQ को क्षेत्रफल
= \(\frac { 1 }{ 2 }\) × आधार × ऊँचाई
= \(\frac { 1 }{ 2 }\) × 4 × 5
= 10 वर्ग सेमी
अत: त्रिभुज APQ का क्षेत्रफल = 10 वर्ग सेमी
![]()
प्रश्न 3.
सिद्ध कीजिए कि त्रिभुज की माध्यिका उसको समन क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।
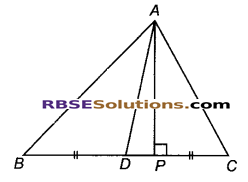
हल:
दिया है : त्रिभुज ABC में, AD भुजा BC पर माध्यिका है।
सिद्ध करना है : ∆ABD का क्षेत्रफल = ∆ADC का क्षेत्रफल
रचना : भुजा BC पर लम्ब AP खींचा।
उपपत्ति : त्रिभुज ABC में,
BD = CD (∵ AD माध्यिका है)
∆ABD का क्षेत्रफल = \(\frac { 1 }{ 2 }\) × BD × AP …(1)
तथा ∆ACD का(RBSESolutions.com)क्षेत्रफल = \(\frac { 1 }{ 2 }\) × CD × AP
∆ACD का क्षेत्रफल = \(\frac { 1 }{ 2 }\) × BD × AP …(2) [∵ CD = BD]
समीकरण (1) तथा (2) से,
∆ABD का क्षेत्रफल = ∆ACD का क्षेत्रफल
इति सिद्धम्।
![]()
प्रश्न 4.
किसी चतुर्भुज के चारों कोणों का योगफल चार समकोण के बराबर होता है।
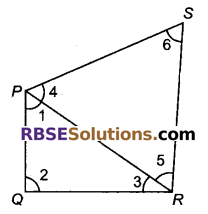
हल:
चित्र में, PQRS एक चतुर्भुज है। इसके चारे कोण ∠P, ∠Q, ∠R एवं ∠S हैं।
PR रेखा चतुर्भुज को दो त्रिभुजों में बाँट रही है।
∆PQR में,
∠1 + ∠2 + ∠3 = 180° …(i)
एवं ∆PSR में,
∠4 + ∠5 + ∠6 = 180° …(ii)
समीकरण (i) तथा (ii) से, को जोड़ने(RBSESolutions.com)पर।
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360°
या (∠1 + ∠4) + ∠2 + (∠3 + ∠5) + ∠6 = 360°
या ∠P + ∠Q + ∠R + ∠S = 4 × 90°
∠P + ∠Q + ∠R + ∠S = 4 समकोण
अतः चतुर्भुज के चारों कोणों(RBSESolutions.com)का योगफल चार समकोण के बराबर होता है।
इति सिद्धम्।
![]()
प्रश्न 5.
एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इसे चतुर्भुज के सभी कोण ज्ञात कीजिए।
हल:
माना चतुर्भुज के चारों कोण 3x, 5x, 9x और 13x है।
अत: 3x + 5x + 9x + 13x = 360°
⇒ 30x = 360°
⇒ x = 12°
पहला कोण = 3 × 12° = 36°
दूसरा कोण = 5 × 12° = 60°
तीसरा कोण = 9 × 12° = 108°
चौथा कोण = 13 × 12° = 156°
अतः चार कोण 36°, 60°, 108° और 156° हैं।
प्रश्न 6.
किसी समान्तर चतुर्भुज के(RBSESolutions.com)विकर्ण बराबर और लम्बवत् हों तो वह एक वर्ग होता है।
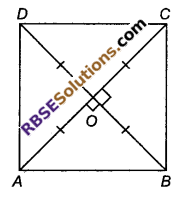
हल:
दिया है: ABCD एक समान्तर चतुर्भुज है जिसके विकर्ण AC और BD हैं जो O बिन्दु पर मिलते हैं।
तथा (i) AC = BD
और (ii) ∠AOB = 90°
सिद्ध करना है: ABCD एक वर्ग है।
उपपत्तिः AC = BD (दिया हुआ है)
⇒ \(\frac { 1 }{ 2 }\) AC = \(\frac { 1 }{ 2 }\) BD
⇒ AO = BO = CO = DO (समान्तर चतुर्भुज(RBSESolutions.com)च० के विकर्ण परस्पर समद्विभाजित करते हैं।)
ΔAOB में,
AO = BO
⇒ ∠BAO = ∠ABO
∠AOB + ∠BAO + ∠ABO = 180°
⇒ 90° + ∠BAO + ∠BAO = 180°
⇒ 2∠BAO = 90°
⇒ ∠BAO = 45°
⇒ ∠BAO = ∠ABO = 45° …..(1)
इसी प्रकार ΔBOC में,
∠CBO = ∠BCO = 45° …(2)
⇒ ∠ABO + ∠CBO = 45° + 45°
⇒ ∠B = 90° ……(3)
⇒ ∠BAO + ∠CBO = 45° + 45° = 90° = ∠B …(4)
समी (3) तथा (4) को जोड़ने पर
∠B + ∠B = 90° + 90°
⇒ 2∠B = 180°
⇒ ∠B = 90° …(5)
ΔABO और ΔADO में,
BO = OD
∠AOB = ∠AOD = 90° (दिया है)
तथा AO = OA (उभयनिष्ठ भुजा)
ΔABO = ΔADO (ASA नियम से)
AB = AD …(6)
(5) और (6) से, ABCD एक वर्ग है।
![]()
प्रश्न 7.
यदि एक समान्तर चतुर्भुज के विकर्ण(RBSESolutions.com)बराबर हों, तो दर्शाइये कि वह एक आयत है।
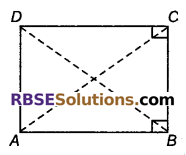
हलः
दिया है : समान्तर चतुर्भुज ABCD में, AC = BD
सिद्ध करना है : ABCD एक आयत है।
उपपत्ति: ΔABC और ΔDCB में ज्ञात है।
AB = DC (सम्मुख भुजाएँ)
BC = BC (उभयनिष्ठ भुजा)
AC = DB (दिया है)
सर्वांगसमता के SSS गुण द्वारा,
ΔABC = ΔDCB
⇒ ∠ABC = ∠DCB …(i)
(सर्वांगसम त्रिभुजों(RBSESolutions.com)के संगत भाग बराबर होते हैं)
लेकिन AB || DC और BC उनको काटती है।
∠ABC + ∠DCB = 180° …(ii)
(क्रमागत अन्त: कोणों का योग 180° होता है)
⇒ 2∠ABC = 180° [∵ ∠DCB = ∠ABC]
⇒ ∠ABC = 90°
अतः ∠ABC = ∠DCB = 90°
ABCD एक समान्तर चतुर्भुज है, जिसका एक कोण 90° है।
अत: ABCD एक आयत है।
इति सिद्धम्।
![]()
प्रश्न 8.
समान्तर चतुर्भुज ABCD के विकर्ण BD पर A और C से डाले गए लम्ब क्रमश: AP तथा CQ हैं। सिद्ध कीजिए कि AP = CQ
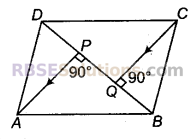
हल:
सिद्ध करना है : AP = CQ
उपपत्तिः समान्तर चतुर्भुज का विकर्ण, समान्तर चतुर्भुज के क्षेत्रफल को दो समान भागों में बाँटता है।
ΔABD का(RBSESolutions.com)क्षेत्रफल = ΔBDC का क्षेत्रफल
हम जानते हैं कि त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) × आधार × ऊँचाई
⇒ \(\frac { 1 }{ 2 }\) × BD × AP = \(\frac { 1 }{ 2 }\) × BD × CQ
⇒ AP = CQ
इति सिद्धम्।
प्रश्न 9.
समान्तर चतुर्भुज ABCD में विकर्ण BD पर दो बिन्दु P और Q इस प्रकार स्थित हैं कि DP = BQ सिद्ध कजिए कि APCQ एक समान्तर चतुर्भुज है।
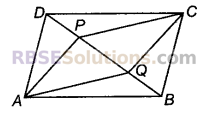
हल:
दिया है : समान्तर चतुर्भुज ABCD के विकर्ण BD पर दो। बिन्दु P और Q इस प्रकार स्थित हैं कि DP = BQ.
सिद्ध करना है : APCQ एक समान्तर चतुर्भुज है।
उपपत्ति : ΔAPD और ΔCQB में,
AD = BC (सम्मुख भुजाएँ)
∠ADP = ∠CBQ (एकान्तर कोण)
DP = BQ (दिया है)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से,
ΔAPD = ΔCQB
अतः सर्वांगसम त्रिभुजों(RBSESolutions.com)की संगत भुजाएँ समान होंगी।
अतः AP = CQ …(1)
इसी प्रकार ΔCPD और ΔAQB में, हम सिद्ध कर सकते हैं कि CP = AQ …(2)
समीकरण (1) और (2) से,
APCQ एक समान्तर चतुर्भुज है।
इति सिद्धम्।
![]()
We hope the given RBSE Solutions for Class 9 Maths Chapter 9 चतुर्भुज Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Chapter 9 चतुर्भुज Additional Questions, drop a comment below and we will get back to you at the earliest.