RBSE Solutions for Class 10 Maths Chapter 12 Circle Additional Questions

RBSE Solutions for Class 10 Maths Chapter 12 Circle Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 12 Circle Additional Questions.

Rajasthan Board RBSE Class 10 Maths Chapter 12 Circle Additional Questions

Multiple Choice Questions
Question 1.
By same arcs of similar circles, angles subtended at the centers are :
(A) equal
(B) half
(C) double
(D) four times
Solution :
(A) is correct.

Question 2.
Arcs cut by equal chords of a circle are:
(A) equal
(B) double
(C) half
(D) triple
Solution :
(A) is correct.

Question 3.
Degree measure of minor arc is :
(A) less than 180°
(B) more than 180°
(C) 270°
(D) 360°
Solution :
(A) is correct.

Question 4.
Degree measure of major arc is :
(A) less than 180°
(B) more than 180°
(C) 270°
(D) 360°
Solution :
(B) is correct.

Question 5.
Sum of opposite angles in a cyclic quadrilateral is :
(A) 270°
(B) 360°
(C) 180°
(D) 90°
Solution :
(C) is correct.

Question 6.
In figure, ∠BAC will be :

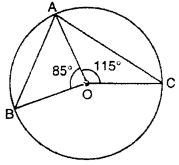
(A) 80°
(B) 160°
(C) 90°
(D) 200°
Solution :
We know that sum of angles at center is 360°.
∠BOC – ∠BOA + ∠COA = 360°
⇒ ∠BOC + 85° + 115° = 360°
⇒ ∠BOC + 200° = 360°
∴ ∠BOC = 360° – 200° = 160°
Angle subtended at center of a circle is double the angle at remaining part by same arc.
∠BOC = 2∠BAC
⇒ ∠BOC = \(\frac { \angle BOC }{ 2 } \) = \(\frac { { 160 }^{ \circ } }{ 2 } \)
∴ ∠BAC = 80°
Hence (A) is correct.

Question 7.
In fig, if O is center of circle, then ∠AOB will be :

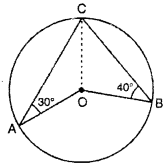
(A) 70°
(B) 110°
(C) 120°
(D) 140°
Solution :
Join CO
In ∆AOC, AO = CO (Radius of same circle)
⇒ ∠OAC = ∠OCA
∴ ∠OCA = 30°
In ∆OCA
∠AOC + ∠OCA + ∠OAC = 180°
[∵ Sum of all the angles of triangle is 180°]
⇒ ∠AOC + 30° + 30° = 180°
⇒ ∠AOC + 60° = 180°
∴ ∠AOC = 180° – 60° = 120°
Similarly, OB = OC
∠OBC = ∠OCB = 40°
In ∆OBC
∠BOC + ∠OBC + ∠OCB = 180°
⇒ ∠BOC + 40° + 40° = 180°
∴ ∠BOC = 180° – 80° = 100°
∴ ∠AOB = 360° – (∠AOC + ∠BOC)
= 360° – (120° + 100°)
= 360° – 220°
∠AOB = 140°
Thus, (D) is correct.

Question 8.
In fig, x will be :

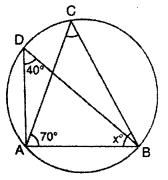
(A) 40°
(B) 70°
(C) 110°
(D) 90°
Solution :
∠ADB and ∠ACB are angles subtended by same arc in same segment so they arc equal.
⇒ ∠ADB = ∠ACB = 40°
∴ ∠ACB = 40 [∵ ∠ADB = 40°, given]
In ∆ABC
∠ABC + ∠ACB + ∠BAC = 180°
[∵ sum of three angles of a triangle is 180°]
⇒ x° + 40° + 70° = 180°
x° + 110° = 180°
x° = 180° – 110° = 70°
Thus, (B) ¡s correct.

Question 9.
In fig, ABCD is a cyclic quadrilateral if ∠D = 120°, then ∠CBE will be :

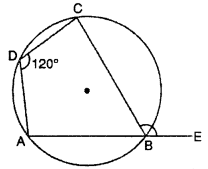
(A) 120°
(B) 60°
(C) 180°
(D) 90°
Solution :
We know that one side of a cyclic quadrilateral is produced, then exterior angle so formed is equal to opposite interior angle.
∠CBE = ∠ADC = 120° [∵ ∠ADC = 120°, given]
Thus, (A) is correct.

Question 10.
In fig, if A, B, C and D are vertices of cyclic quadrilateral, then will be :

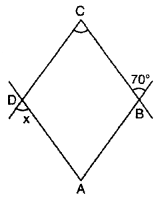
(A) 70°
(B) 35°
(C) 110°
(D) 100°
Solution :
∵ ∠CBA + 70° = 180° (linear pair)
∠CBA = 180° – 70° = 110°
∵ ABCD is cyclic quadrilateral
We know that sum of opposite angles of cyclic quadrilateral is 180°
Thus, ∠CBA + ∠CDA = 180°
⇒ 110° + ∠CDA = 180°
⇒ ∠CDA = 180° – 110°
= 70°
But ∠x + ∠CDA = 180° (linear pair)
∠x + 70° = 180°
∠x = 180° – 70°
= 110°
Thus, (C) is correct.

Question 11.
The diameter of a circle is 30 cm. If length of one chord is 20 cm, then distance of chord from center will be:
(A) 5\(\sqrt { 5 }\) cm
(B) 5 cm
(C) 3 \(\sqrt { 5 }\) cm
(D) 2 \(\sqrt { 5 }\) cm
Solution :
Diameter of circle = 30 cm
Radius of circle = \(\frac { 30 }{ 2 }\) = 15 cm
AP = PB = \(\frac { 20 }{ 2 }\) = 10 cm [∵ OP ⊥ AB]

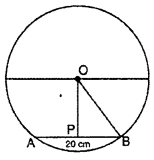
In right angled ∆OPB
OB² = OP² + PB²
15² = OP² + 10²
225 = OP² + 100
OP² = 125
OP = \(\sqrt { 125 }\)
OP = 5 \(\sqrt { 5 }\) cm
Thus, (A) is correct.

Question 12.
In the given figure, O is centre of the ∠APB = 40°, then value of ∠AQB will be :

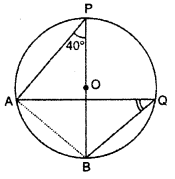
(A) 90°
(B) 50°
(C) 40°
(D) 100°
Solution :
Join AB, We know that angle subtended by same chord in a circle are equal Thus, ∠APB and ∠AQB will be same
Thus ∠APB = ∠AQB = 40°
∴ ∠AQB = 40°
Thus, (C) is correct.

Question 13.
In figure, O is center of circle and ∠PQR = 115° ∠POR will be :

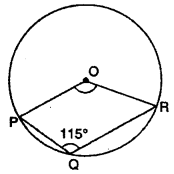
(A) 130°
(B) 230°
(C) 270°
(D) 360°
Solution :
Major angle ∠POR = 2∠PQR
x = 2 × 115°
x = 230°
Sum of angles formed at center of circle is 360°

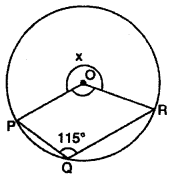
∴ ∠POR + x = 360°
∠POR + 230° = 360°
∠POR = 360° – 230°
∠POR = 130°
Thus, (A) is correct.

Question 14.
In figure, chords AB and CD of circle with center O, arc same. If ∠AOB = 55°, then ∠COD will be :

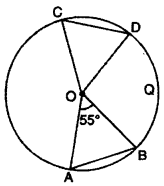
(A) 110°
(B) 75°
(C) 90°
(D) 55°
Solution :
Chord AB = Chord CD
\(\widehat { AB }\) = \(\widehat { CD }\)
∠AOB = ∠COD
∠COD = 55° [∵ ∠DOB = 55°]
Thus, (D) is correct.

Question 15.
In fig, D is cyclic quadrilateral in which AC and BD are diagonals. If ∠DBC = 55° and ∠BAC = 45°, then ∠BCD will be :

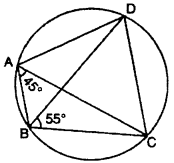
(A) 80°
(B) 90°
(C) 110°
(D) 115°
Solution :
∠CAD = ∠DBC = 55° (angles of same segment)
∴ ∠DAB = ∠CAD + ∠BAC
55°+ 45° = 110°
But ∠DAB + ∠BCD = 180° (opposite angles of cyclic quadrilateral)
similarly, ∠BCD = 180° – 100° = 80°
Thus, (A) is correct.

Question 16.
If in given fig. ΔABC is an equilateral triangle, then ∠BCD will be :

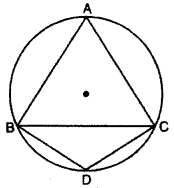
(A) 140°
(B) 120°
(C) 180°
(D) 275°
Solution :
In ΔABC ∠A = 60° and in cyclic quadrilateral ABCD ∠A + ∠D = 180°
∠D = 180° – ∠A
= 180° – 60°
∠BDC = 120°
Thus, (B) is correct.

Question 17.
A circle is of radius 5 cm. Its longest chord will be :
(A) 5 cm
(B) 8 cm
(C) 10 cm
(D) 15 cm
Solution :
Diameter = longest chord
= 2 × radius = 2 × 5
= 10 cm
Thus, (C) is correct.

Question 18.
If 16 cm long chord is at a distance of 6 cm from the center of circle, then radius of circle will be :
(A) 10 cm
(B) 5 cm
(C) 10 cm
(D) 15 cm
Solution :
In ∆AOP

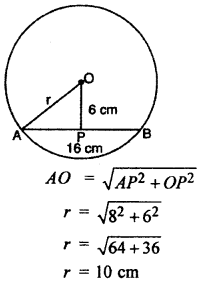
Thus, (C) is correct.

Question 19.
In given fig., O is center of the circle. Chord AB = CD and ∠OBA = 40°, then ∠COD will be :

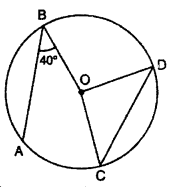
(A) 100°
(B) 80°
(C) 180°
(D) 90°
Solution :
Given : AB = CD
Radius of circle = OB = OD
∴ ∠OBA = ∠ODC = 40°
∆OCD in OD = OC (Radius of circle)
∴ ∆OCD is an isosceles triangle.
∠OCD = ∠ODC = 40°
In ∆OCD,
∠ODC + ∠OCD + ∠COD = 180°
40° + 40° + ∠CQD = 180°
∠COD = 180° – 40° – 40°
∠COD = 180° – 80°
∠COD = 100°
Thus, (A) is correct.

Question 20.
In figure, ABCD Is s cyclic quadrilateral whose diagonals intersect each other at O. If ∠ACB = 50° and ∠ABC = 110°, then ∠BDC will be :

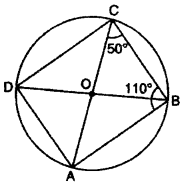
(A) 110°
(B) 60°
(C) 40°
(D) 20°
Solution :
∵ Angles formed in alternate segment by arc AB
∠ADB = ∠ACB
∠ADB = 50° [∵ ∠ACB = 50°]
We know that sum of opposite angles of cyclic quadrilateral is 180°
∴ ∠ADC + ∠ABC = 180°
∠ADC + 1100 1 80°[∵ ∠ABC = 110°]
∠ADC = 180° – 110° = 70°
Now ∠ADC = ∠ADB + ∠BDC
70° = 50° + ∠BDC
70° – 50° = ∠BDC
20° = ∠BDC
Thus, ∠BDC = 20°
Thus, (D) is correct.

Short Answer/Long Answer Type Questions
Question 1.
In fig. O is centre of circle and OC is bisector of ∠ACB. If AC = 4 cm, tien find BC.

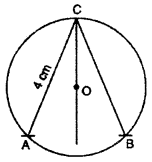
Solution : Join OA and OB
In ∆OCA and ∆OCB
OA = OB (Same radius of circle)
OC = OC (common)
∠ACO = ∠BCO
(∵ OC, is bisector of ∠ACB)
Thus, by SAS congruence criterion

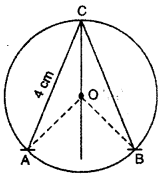
∆OCA = ∆OCB
By CPCT
AC = BC = 4
4 = BC
or BC = 4 cm

Question 2.
Two circles of radius 5 cm and 4 cm cut each other at A and B. If common chord AB 6 cm, then find distance between their centers.
Solution :
Let two circles with center O and O’ and radius 4 cm and 5 cm. respectively and AB is common chord.
OA = 5 cm O’A = 4 cm AB = 6 cm
∴ AL = \(\frac { 1 }{ 2 }\)AB = \(\frac { 1 }{ 2 }\) × 6 = 3 cm
In right angled ∆OLA
OA² = OL² + AL²
(5)² = OL² + (3)²
OL² = (5)² – (3)²
OL² = 25 – 9
OL² = 16
OL = \(\sqrt { 16 }\) = 4

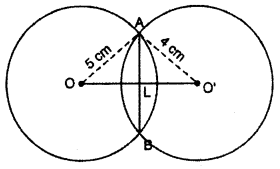
In right angled ∆O’LA
O’A² =O’L² + AL²
(4)² = O’L² + (3)²
16 = O’L² + 9
O’L² = 16 – 9 = 7
O’L = \(\sqrt { 7 }\) =2.6457
O’L = 2.65 (approx)
OO’ = OL + O’L
OO’ = 4 + 2.65 = 6.65 cm

Question 3.
In fig. AN = 8 cm and CD = 6 cm are two parallel chords of a circle with center O, find the distance between these chords.

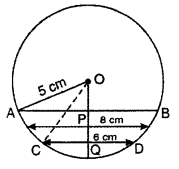
Solution :
AB = 8 cm (given)
AP = \(\frac { 8 }{ 2 }\) = 4 cm
CD = 6 cm
CQ = \(\frac { 6 }{ 2 }\) = 3 cm
Radius OA = OC = 5 cm
In right angled ∆OCQ
OC² + OQ² + QC²
5² = OQ² + 3²
OQ² = 5² – 3²
OQ² = 25 – 9 = 16
OQ = 4 cm
In right angled ∆AOP
AO² = OP² + AP²
5² = OP² + 4²
OP² = 5² – 4²
= 25 – 16 = 9
OP = 3 cm
Thus, distance between two parallel lines
PQ = OQ – OP
= 4 – 3 = 1 cm
Thus, PQ = 1 cm

Question 4.
In fig, AB is a chord of a circle with center O. If ∠ACD = 40°, then find ∠OAB.

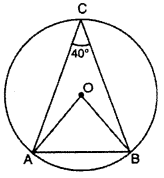
Solution :
We know that angle subtended by arc at the center of circle is double the angle subtended at remaining part of circle.
∠AOB = 2∠ACB
∠AOB = 2 × 40° [∵ ∠ACB = 40°]
∠AOB = 80°
OA = OB (Radius of circle)
∴ ∠OAB = ∠OBA
In ΔOAB
∠OAB + ∠OBA + ∠AOB = 180°
∠OAB + ∠OAB + 90° = 180°
2∠OAB = 180° – 90°
2∠OAB = 90°
∠OAB = \(\frac { { 90 }^{ \circ } }{ 2 } \)
Thus, ∠OAB = 45°.

Question 5.
Prove that If one pair of opposite angles of a quadrilateral is supplementary, then quadrilateral is cyclic :
Solution :
Given : quadrilateral ABCD, in which ∠ABC + ∠ADC = 180° and ∠BAD + ∠BCD = 180°
To Prove : ABCD is a cyclic quadrilateral.
Construction : Draw a circle passing through points A, B, C but not D. But cuts AD at E. Join EC

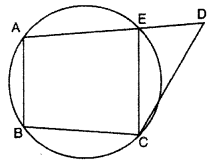
Proof : quadrilateral ABCE is cyclic
Thus, ∠ABC + ∠AEC = 180° …..(i)
But given that
∠ABC + ∠ADC = 1800 ……(ii)
From equations (i) and (ii)
∠AEC = ∠ADC ……(iii)
But It is impossible because one is exterior and other is interior angle of ΔCED. it is possible only when D and E coincides so circle will pass through A, B, C and D i.e., ABCD is a cyclic quadrilateral.

Question 6.
Prove that line joining the mid point of hypotenuse of right angled triangle to opposite vertex is half the hypotenuse.

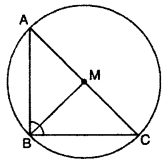
Solution :
Given : In right angled ΔABC
∠ABC = 90° and point M is mid point of hypotenuse AC
To Prove : BM = AM = CM
Construction : Taking AC as a diameter draw a circle which passes through B.
Proof : Hypotenuse AC diameter circle, of right ΔABC, AC is
M is mid point of AC so M will be center of circle
Thus, AM = MC …(i) [M is mid point]
BM = MC ….(ii) [Radius of circle]
From equations (i) and (ii)
BM = AM = MC = \(\frac { 1 }{ 2 }\)AC,

Question 7.
In fig, O is center of circle and AB || CD, if ∠ADC = 25°, then find ∠AEB.

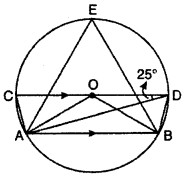
Solution :
Join CA and BD, we know that angle subtended by arc at center of the circle is double the angle at remaining part by same arc
Thus ∠AOC = 2∠ADC
= 2 × 25°
∠AOC = 50°
Now AB || CD and AO is transversal. We know that line AO, intersects CD and AB at O and A respectively such that ∠OAB = ∠AOC and ∠OAB = 50°
In ∆OAB
OA = OB (radius of circle)
⇒ ∠OAB = ∠OBA(In a triangle angles opposite to equal sides arc equal)
⇒ ∠OBA = ∠OAB
⇒ ∠OBA = 50°
in ∆OAB
∠OAB + ∠OBA + ∠AOB = 180° [∵ Sum of triangle angles of a triangle ∆ is 180°]
50° + 50° + ∠AOB = 180°
100° + ∠AOB = 180°
∠AOB = 180°- 100°
∠AOB = 80°
Again, we know that angle subtended by an arc at center is double the angle at remaining part of circle by same arc.
∴ ∠AOB = 2∠AEB
⇒ 80° = 2∠AEB
⇒ ∠AEB = \(\frac { { 80 }^{ \circ } }{ 2 } \) = 40°

Question 8.
Two diameters of a circle intersect at 90°, prove that by joining their internal points, quadrilateral so formed will be a square.
Solution :
Given : Two diameters AB and CD intersect each other at 90°
To Prove : ACBD is a square.

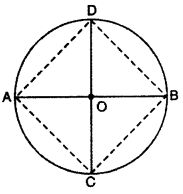
Construction : AC. CB, BD, AD.
Proof : ∵ Two diameter passes through center and O is mid point of two diameters
OA = OB = OC = OD [radius of circle]
in ΔAOD and ΔBOC
AO = BO (radius of circle)
∠AOD = ∠BOC [each 90° (given)]
OD = OC
By SAS congruence criterion
ΔAOD = ΔBOC
AD = BC …..(i)
Similarly in ΔAOC and ΔBOD
AC = BC …..(ii)
In ΔBOC and ∠BOD
BO = BO (common side)
∠BOC = ∠BOD (each 90° given)
OC = OD (radius of circle)
By SAS congruence criterion
ΔBOC = ΔBOD
⇒ BC = BD …..(iii)
From equations (i), (ii) and (iii)
AD = BC = AC = BD …..(iv)
i.e., four sides are equal Thus, ∠A, ∠B, ∠C and ∠D are angles in semicircle.
But angle in semicircle is of 90°
∴ ∠A = ∠B = ∠C = ∠D = 90° ……(v)
Thus, from equations (iv) and (v)
ACBD is a square.

Question 9.
Find x, for each of the following –

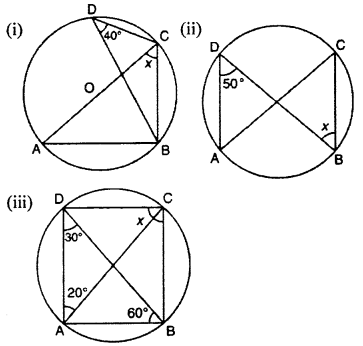
Solution :
We know that angles subtended by same arc at two point of remaining parts arc equal.

Here ∠BAC and ∠BDC are angles of same segment.
Thus, ∠BAC = ∠BDC [∠BDC = 40°]
∠BAC = 40°
Now ∠ABC, is an angle in semicircle, So ∠ABC = 90°
In ΔABC
∠ABC + ∠BAC + ∠ACB = 180° [∵ sum of three angles of a triangle is 180°]
90° + 40° + x = 180°
130° + x = 180°
x = 180° – 130° = 50°

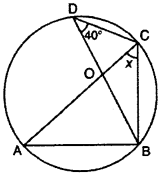
(ii) In ΔOBC, OB = OC (radius of circle)
∠OBC = ∠OCB
∴ ∠OBC = ∠OBC = x
We know that angles subtended by same arc at two points of remaining parts are equal

⇒ ∠ADB = ∠ACB
⇒ ∠ACB = ∠ADB = 50° [∵ ∠ACB = ∠OCB = x]
∠x = 50°

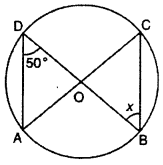
(iii) We know that angles in same segment are equal
∠ADB and ∠ACB are angles of same segment
Thus, ∠ACB = ∠ADB [∵ ∠ADB = 30°] (given)
∠ACB = 30° ……(i)
Angle of same segment are equal .
∠ACD and ∠DBA are angles of same segment.

∠ACD = ∠DBA
∠ACD = 60° [∵ ∠DBA = 60°] …..(ii)
x = ∠ACB + ∠ACD
From equation (i) and (ii)
x = 30° + 60°
x = 90°.

Question 10.
In fig. chord AB bisects chord CD at O, Prove that –
OA² = DO·OC
Solution :
Given : chord AB bisects chord CD at O
CO = OD …..(i)
Join BC
∠CAB and ∠BDC, arc angles of same segment so will be equal

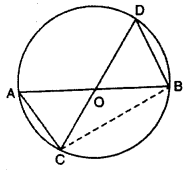
∠CAB = ∠BDC …..(ii)
In ∆COA and ∆DOB
∠CAO = ∠BDO (from equation (ii))
CO = OD (given eqn. (i)
∠COA = ∠DOB( vertically opposite angles)
By ASA congruence rule.
∆COA = ∆DOB
Thus, corresponding sides of congruent triangle are same
OA = OB
OB = OC [∵ OB and OC, arc radius of circle]
OA = OC
(OA)² = (OC)²
(OA)² = OC² × OC²
OA² =OC × OD [OC = OD]
or OA² = DO × OC

Question 11.
Prove that two arcs of circle are congruent if angles subtended by them at center arc equal.
Solution :
Given : A circle with center O and two angles formed at center.

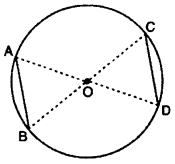
∠AOB = ∠COD ……(i)
To Prove : \(\widehat { AB }\) = \(\widehat { CD }\)
Construction : Join OA, OB, OC and OD by center O.
Proof : In ∆AOB and ∆COD (given)
AO = OD (radius of circle)
OB = OC (radius of circle)
∠AOB = ∠COD (given)
By SAS congruence criterion
∆AOB = ∆COD
Thus, By CPCT
AB = CD
Chord AB = Chord CD and AB = CD

Question 12.
If sum of angle subtended by arc at center and at circumference is 108°, then find the angle at center and at circumference.
Solution :
In circle C(O, r) angle subtended by arc PQ at center ∠POQ and internal angle in alternate segment is ∠PRQ

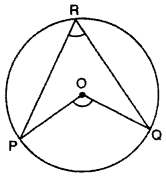
∠POQ + ∠PRQ = 108°
We know that angle subtended by arc at center of circle ¡s double the angle at remaining part.
∠POQ = 2∠PRQ …..(i)
But ∠POQ + ∠PRQ = 108°
2∠PRQ + ∠PRQ = 108°
3∠PRQ = 108°
∠PRQ = \(\frac { { 108 }^{ \circ } }{ 2 } \) = 36°
∠PRQ pulling value of in equation (i)
∠POQ = 2∠PRQ = 2 × 36 = 72°
Angle at center of circle = 72° and angle of remaining part = 36°.

Question 13.
In figure, PARS is cyclic quadrilateral whose diagonal intersect at A if ∠SQR = 80° and ∠QPR = 30°, then find ∠SRQ.

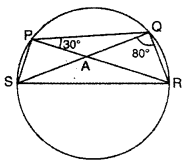
Solution :
Given : ∠SQR = 80°
Now ∠SQR = ∠SPR [angles of same segment]
∴ ∠SPR = 80°
∴ ∠SPQ = ∠SPR + ∠RPQ
= 80° + 30°
or ∠SPQ = 110°
but ∠SPQ + ∠SRQ = 180° [Sum of opposite angles of cyclic quadrilateral]
∴ ∠SRQ = 180° – ∠SPQ
= 180° – 110° = 70°
Thus, ∠SRQ = 70°

Question 14.
The bisectors of angle A, B and C of a ∆ABC intersect its circumcricle at D, E and F respectively, Prove that angles of ∆DEF arc 90° – \(\frac { 1 }{ 2 }\)A, 90° – \(\frac { 1 }{ 2 }\)B and 90° – \(\frac { 1 }{ 2 }\) C.
Solution :
According to question AD is bisector of ∠A

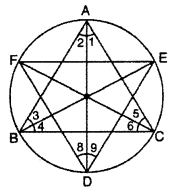
∴ ∠1 = ∠2 = \(\frac { A }{ 2 }\)
BE, is bisector of ∠B
∴ ∠3 = ∠4 = \(\frac { B }{ 2 }\)
CF, is bisector of ∠C
∴ ∠5 = ∠6 = \(\frac { C }{ 2 }\)
We know that angles in same segment are equal.

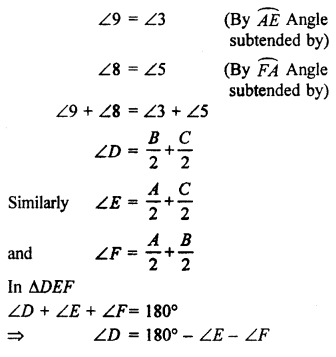
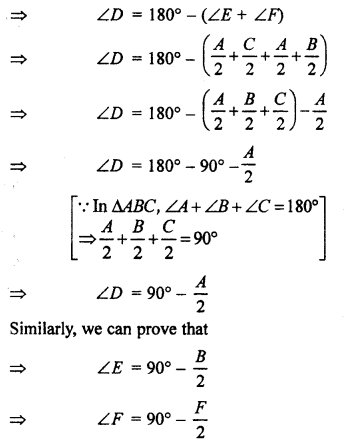
We hope the given RBSE Solutions for Class 10 Maths Chapter 12 Circle Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 12 Circle Additional Questions, drop a comment below and we will get back to you at the earliest.