RBSE Solutions for Class 10 Maths Chapter 12 Circle Ex 12.4 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 12 Circle Exercise 12.4.
Rajasthan Board RBSE Class 10 Maths Chapter 12 Circle Ex 12.4
Question 1.
An angle of a cyclic (RBSESolutions.com) quadrilateral is given find its opposite angle.
(i) 70°
(ii) 135°
(iii) 112\(\frac { 1 }{ 2 } \circ \)
(iv) \(\frac { 3 }{ 5 }\) right angle
(v) 165°
Solution :
(i) We know that sum of opposite angles of a cyclic quadrilateral is 180°. Let opposite angle be x°, then
70° + x° = 180°
x° = 180° – 70° = 1 10°
(ii) ∵ Sum of opposite angles of a cyclic quadrilateral is 180°
Let other angle be x°
x° + 135° = 180°
x° = 180°- 13° = 45°
(iii) ∵ Sum of opposite angles of a cyclic quadrilateral is 180°
Let other angle be x°
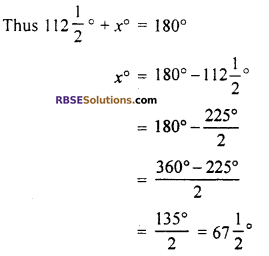
(iv) Given : first angle = \(\frac { 3 }{ 5 }\) rectangle = \(\frac { 3 }{ 5 }\) × 90° =3 × 18 = 54°
∵ Sum of opposite (RBSESolutions.com) angles of a cyclic quadrilateral is 180°
Let other angle be x°
x° + 540 = 180°
x° = 180° – 54° = 126°
(v) Let other angle = x°
Sum of opposite angles of a cyclic quadrilateral is 180°
x° + 165° = 180°
x° = 180° – 165° = 15°
![]()
Question 2.
Find opposite angle of cyclic (RBSESolutions.com) quadrilateral if one angle is (i) \(\frac { 2 }{ 7 }\) of other
(ii) \(\frac { 11 }{ 4 }\) of other.
Solution :
(i) Let other opposite angle
So, according to question, first opposite = \(\frac { 2 }{ 7 }\)x
We know that sum of opposite angles of cyclic quadrilateral is 180°
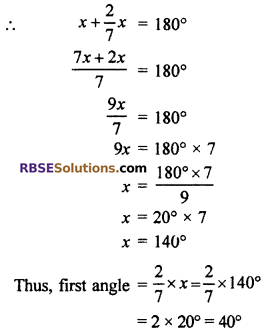
Thus, opposite angles of cyclic quadrilateral will be 40°, 140°.
(ii) Let other opposite ∠ = x°
Thus according to question., (RBSESolutions.com) first opposite ∠ = x × \(\frac { 11 }{ 4 }\) = \(\frac { 11x }{ 4 }\)
We know that sum of opposite angles of cyclic quadrilateral is 180°

Thus, opposite angles of cyclic quadrilateral will be 132°, 48°.
Question 3.
In figure, find all the (RBSESolutions.com) four angles of cyclic.
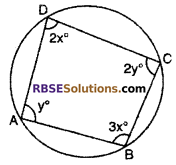
Solution :
We know that sum of opposite angles of cyclic quadrilateral is 180°

Question 4.
In figure, some angles are (RBSESolutions.com) marked a, b, c and d, find them.
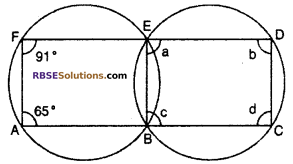
Solution :
ABEF and BCDE arc cyclic quadrilateral
∵ We know that sum of opposite angles of cyclic quadrilateral is 180°
Thus, ∠FAB + ∠BEF = 180°
65° + ∠BEF = 180°
∠BEF = 180° – 65° = 115°
and ∠EBA + ∠AFE = 180°
∠EBA + 91° = 180°
∠EBA = 180° – 91° = 89°
We know that exterior angle of (RBSESolutions.com) cyclic quadrilateral is equal to internal opposite angle
Thus ∠EBC = ∠AFE = 91°
∴ ∠EBC = c = 91°
∠DEB = ∠BAF = 65° = a = 65°
∠EBA = ∠CDE = 89°
∠CDE = b = 89°
∴ ∠BEF = ∠BCD= 115°
∴ ∠BCD = d = 115°
Thus, ∠a = 65°, ∠b = 89°, ∠c = 91°, ∠d = 115°.
Question 5.
If in cyclic quadrilateral ABCD, AD || BC, then Prove that ∠A = ∠D.
Solution :
Given :
ABCD is a cyclic quadrilateral on which AD || BC
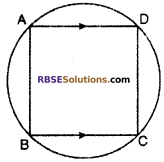
To Proved :
∠A = ∠D
Proof : ABCD is a cyclic quadrilateral
We know that sum of opposite (RBSESolutions.com) angles of a cyclic quadrilateral is 180°
∠A + ∠C = 180°
and ∠B + ∠D = 180° ….(ii)
but ∠A + ∠B = 180° (co-interior corresponding angles) (iii)
From equation (ii) and (iii)
⇒ 2∠A + ∠B + ∠C = ∠B + ∠C + 2∠D
⇒ 2∠A = 2∠D
⇒ ∠A = ∠D
![]()
Question 6.
ABCD is a cyclic quadrilateral. (RBSESolutions.com) produced AB and DC meet at E. Prove that ∆EBNC and ∆EOA arc similar.
Solution :
Given :
ABCD is a cyclic quadrilateral. Produced AB and DC meet at F.
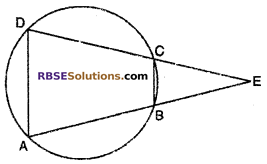
To Prove : ∆EBC ~ ∆EDA
In ∆EBC and ∆EDA
∠EBC = ∠EDA [∵ Exterior of cyclic quadrilateral is equal to interior opposite angle.]
∠ECB = ∠EAD [∵ Exterior of cyclic (RBSESolutions.com) quadrilateral is equal to interior opposite angle.]
∠E = ∠E (Common angle)
Thus, by AAA similarly
∆EBC ~ ∆EDA
Question 7.
Prove that angle bisectors of cyclic quadrilaterals formed a cyclic quadrilateral.
Solution :
Given :
A cyclic quadrilateral ABCD.
AP, BP, CR and DR are respectively bisector of
∠A, ∠B, ∠C, and ∠D.
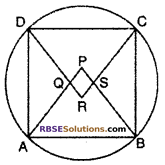
To Proved : PQRS is a cyclic quadrilateral.
Proof : To Prove PQRS a (RBSESolutions.com) cyclic quadrilateral, we should prove
∠APB + ∠CRD = 180°
We know that sum of opposite angles of a cyclic quadrilateral is 180°
Now in ∆APB and ∆CRD


⇒ One pair of opposite angles of (RBSESolutions.com) quadrilateral PQRS arc supplementary.
⇒ PQRS is a cyclic quadrilateral.
![]()
We hope the given RBSE Solutions for Class 10 Maths Chapter 12 Circle Ex 12.4 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 12 Circle Exercise 12.4, drop a comment below and we will get back to you at the earliest.