RBSE Solutions for Class 10 Maths Chapter 17 केन्द्रीय प्रवृत्ति के माप Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 17 केन्द्रीय प्रवृत्ति के माप Additional Questions.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 17 |
| Chapter Name | केन्द्रीय प्रवृत्ति के माप |
| Exercise | Additional Questions |
| Number of Questions Solved | 57 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 17 केन्द्रीय प्रवृत्ति के माप Additional Questions
विविध प्रश्नमाला 17
निम्न प्रश्नों के उत्तरों के चार संभावित विकल्प दिए हुए हैं। सही उत्तर वाले विकल्प का चुनाव कीजिए।
प्रश्न 1.
किसी श्रेणी का बहुलक मूल्य (RBSESolutions.com) होता है
(क) मध्यवर्ती मूल्य
(ख) सर्वाधिक बारम्बारता वाला मूल्य
(ग) न्यूनतम बारम्बारता मूल्य
(घ) सीमान्त मूल्य
उत्तर:
(ख) सर्वाधिक बारम्बारता वाला मूल्य
प्रश्न 2.
निम्न श्रेणी का माध्यक मूल्य है 520, 20, 340, 190, 35, 800, 1210, 50, 80
(क) 1210
(ख) 520:
(ग) 190
(घ) 35
उत्तर:
(ग) 190
![]()
प्रश्न 3.
चार छात्रों के सांख्यिकी में प्राप्तांक 53, 75, 42, 70 हैं, (RBSESolutions.com) उनके प्राप्तांकों का समान्तर माध्य है
(क) 42
(ख) 64
(ग) 60
(घ) 56
उत्तर:
(ग) 60
प्रश्न 4.
एक छात्र को गणित, भौतिक विज्ञान तथा रसायन विज्ञान में क्रमशः 85, 87 तथा 83 अंक मिले। उसके इन विषयों में प्राप्तांकों का माध्य है
(क) 86
(ख) 84
(ग) 85
(घ) 85.5
उत्तर:
(ग) 85
प्रश्न 5.
यदि 5, 7, 9, x का समान्तर (RBSESolutions.com) माध्य 9 हो, तो x का मान है
(क) 11
(ख) 15
(ग) 18
(घ) 16
उत्तर:
(ख) 15
प्रश्न 6.
बंटन 2, 3, 4, 7, 5, 1 का माध्यक है
(क) 4
(ख) 7
(ग) 11
(घ) 3.5
उत्तर:
(घ) 3.5
प्रश्न 7.
बंटन 1, 3, 2, 5, 9 का माध्यक है
(क) 3
(ख) 4
(ग) 2
(घ) 20
उत्तर:
(क) 3
प्रश्न 8.
बंटन 3, 5, 7, 4, 2, 1, 4, 3, 4 का (RBSESolutions.com) बहुलक है
(क) 7
(ख) 4
(ग) 3
(घ) 1
उत्तर:
(ख) 4
प्रश्न 9.
किसी स्कूल के छात्रों की संख्या उनकी आयु के अनुसार निम्न प्रकार है इनका बहुलक होगा
| आयु वषों में | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| छात्रों की संख्या | 15 | 25 | 40 | 36 | 41 | 37 | 20 | 13 | 5 | 3 |
(क) 41
(ख) 12
(ग) 3
(घ) 17
उत्तर:
(ख) 12
![]()
निम्न बंटनों को समान्तर माध्य ज्ञात कीजिए-(प्रश्न 10 से 14)
प्रश्न 10.
| X | 5 | 6 | 7 | 8 | 9 |
| f | 4 | 8 | 14 | 11 | 3 |
हल:
समान्तर माध्य के (RBSESolutions.com) लिये सारणी।
| X | f | fx |
| 5 | 4 | 20 |
| 6 | 8 | 48 |
| 7 | 14 | 98 |
| 8 | 11 | 88 |
| 9 | 3 | 27 |
| ∑f = 40 | ∑fx = 281 |
समान्तर माध्य \(=\frac{\Sigma f x}{\Sigma f}=\frac{281}{40}=7.025\) उत्तर
प्रश्न 11.
| प्राप्तांक | 10 | 15 | 17 | 20 | 22 | 30 | 35 |
| छात्रों की संख्या | 5 | 10 | 2 | 8 | 3 | 6 | 6 |
हल:
समान्तर माध्य के लिये (RBSESolutions.com) सारणी
| X | f | fx |
| 10 | 5 | 50 |
| 15 | 10 | 150 |
| 17 | 2 | 34 |
| 20 | 8 | 160 |
| 22 | 3 | 66 |
| 30 | 6 | 180 |
| 35 | 6 | 210 |
| ∑f = 40 | ∑fx = 850 |
समान्तर माध्य
\(\begin{array}{l}{\overline{\mathrm{X}}=\frac{\Sigma \mathrm{fx}}{\Sigma \mathrm{f}}} \\ {\overline{\mathrm{X}}=\frac{850}{40}} \\ {\overline{\mathrm{X}}=21.25}\end{array}\) उत्तर
प्रश्न 12.
| X | 19 | 21 | 23 | 25 | 27 | 29 | 31 |
| f | 13 | 15 | 16 | 18 | 16 | 15 | 13 |
हल:
समान्तर माध्य के लिये (RBSESolutions.com) सारणी
| X | f | fx |
| 19 | 13 | 247 |
| 21 | 15 | 315 |
| 23 | 16 | 368 |
| 2.5 | 18 | 450 |
| 27 | 16 | 432 |
| 29 | 15 | 435 |
| 31 | 13 | 403 |
| ∑f = 106 | ∑fx = 2650 |
समान्तर माध्य
\(=\frac{\Sigma f x}{\Sigma f}=\frac{2650}{106}=25\)
प्रश्न 13.
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| f | 45 | 25 | 19 | 8 | 2 | 1 |
हल:
| X | f | fx |
| 1 | 45 | 45 |
| 2 | 25 | 50 |
| 3 | 19 | 57 |
| 4 | 8 | 32 |
| 5 | 2 | 10 |
| 6 | 1 | 06 |
| ∑f = 100 | ∑fx = 200 |
समान्तर माध्य \(=\frac{\Sigma f x}{\Sigma f}=\frac{200}{100}=2\) उत्तर
![]()
प्रश्न 14.
निम्न बारम्बारता बंटन से समान्तर (RBSESolutions.com) माध्य ज्ञात कीजिए
| भार (किग्रा. में) | 40-44 | 44-48 | 48-52 | 52-56 | 56-60 | 60-64 |
| व्यक्तियों की संख्या | 5 | 6 | 5 | 9 | 3 | 2 |
हल:
समान्तर माध्य की गणना के लिये सारणी माना A = 50, h = 4
| भार (किग्रा. में) | (f) | मध्यमान (x) | (f.x) |
| 40-44 | 5 | 42 | 210 |
| 44-48 | 6 | 46 | 276 |
| 48-52 | 5 | 50 | 250 |
| 52-56 | 9 | 54 | 486 |
| 56-60 | 3 | 58 | 174 |
| 60-64 | 2 | 62 | 124 |
| ∑f = 30 | ∑fx = 1520 |
समान्तर माध्य
\(\begin{array}{l}{\overline{\mathrm{X}}=\frac{\Sigma \mathrm{fx}}{\Sigma \mathrm{f}}} \\ {\overline{\mathrm{X}}=\frac{1520}{30}=50.67}\end{array}\) किग्रा. (लगभग)
अतः अभीष्ट समान्तर माध्य = 50.67 उत्तर
निम्न बंटन का माध्यक ज्ञात कीजिए–(प्रश्न 15-16)
प्रश्न 15.
| x | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
| f | 30 | 60 | 20 | 40 | 10 | 50 | 35 |
हल:
बंटन को सारणी के रूप में (RBSESolutions.com) लिखने पर
| X | f | cf |
| 0.1 | 30 | 30 |
| 0.2 | 60 | 90 |
| 0.3 | 20 | 110 |
| 0.4 | 40 | 150 |
| 0.5 | 10 | 160 |
| 0.6 | 50 | 210 |
| 0.7 | 35 | 245 |
| ∑f = 245 |
अब
\(\begin{aligned} \frac{\mathrm{N}}{2} &=\frac{\Sigma \mathrm{f}}{2} \\ &=\frac{245}{2}=122.5 \end{aligned}\)
यह माध्यक 150 संचयी आवृत्ति में होगा जिसका विचर 0.4 है।
अतः माध्यक M = 0.4 उत्तर
प्रश्न 16.
| जूतों की नाप | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 | 8.0 | 8.5 | 9.0 |
| बारम्बारता | 1 | 2 | 4 | 5 | 15 | 30 | 60 | 95 | 82 | 75 |
हल:
बंटन को सारणी के रूप में (RBSESolutions.com) लिखने पर
| X | f | संचयी बारम्बारता (cf) |
| 4.5 | 1 | 1 |
| 5.0 | 2 | 3 |
| 5.5 | 4 | 7 |
| 6.0 | 5 | 12 |
| 6.5 | 15 | 27 |
| 7.0 | 30 | 57 |
| 7.5 | 60 | 117 |
| 8.0 | 95 | 212 |
| 8.5 | 82 | 294 |
| 9.0 | 75 | 369 |
| ∑f = 369 |
माध्यक \(\begin{array}{l}{=\frac{N}{2}} \\ {=\frac{369}{2}} \\ {=184.5}\end{array}\)
184.5 184.5 संचयी बारम्बारता 212 के अन्तर्गत आती है जो कि विचर 8.0 में है।
अतः माध्यक = 8.0 उत्तर
प्रश्न 17.
क्रिकेट की एक टीम के खिलाड़ियों द्वारा बनाए गये (RBSESolutions.com) रनों की संख्या निम्न प्रकार है–
57, 17, 26, 91, 115, 26, 83, 41, 57, 0, 26.
इसका समान्तर माध्य, माध्यक और बहुलक ज्ञात कीजिए।
हल:
(i) समान्तर माध्य-समान्तर माध्य \(\overline{\mathrm{X}}=\frac{\Sigma \mathrm{x}}{\mathrm{n}}\)
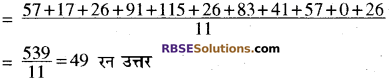
(ii) माध्यक के लिये-विचर की संख्याओं को आरोही क्रम में रखने पर 0, 17, 26, 26, 26, 41, 57, 57, 83, 91, 115
यहाँ n = 11
अतः माध्यक \(M=\frac{n+1}{2}\) वीं संख्या \(=\frac{11+1}{2}\) वीं संख्या = 6वीं संख्या
अतः माध्यक M = 41 रन उत्तर
(iii) बहुलक के लिये
| विचार | 0 | 17 | 26 | 41 | 57 | 83 | 91 | 115 |
| गणन चिह | | | | | | | | | | | | | | | | | | | |
| बारम्बारता | 1 | 1 | 3 | 1 | 2 | 1 | 1 | 1 |
यहाँ पर बारम्बारता 3 अधिकतम है। (RBSESolutions.com) इसके संगत विचर को मान 26 है।
अतः बहुलक = 26 रन उत्तर
![]()
निम्न बारम्बारता बंटन का बहुलक ज्ञात कीजिए (प्रश्न 18-19)
प्रश्न 18.
| वर्ग | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| बारम्बारता | 4 | 7 | 13 | 9 | 3 |
हल:
यहाँ बारम्बारता 13, वर्ग अन्तराल (20-30) की सबसे अधिक है।
अतः यह बहुलक वर्ग होगा।
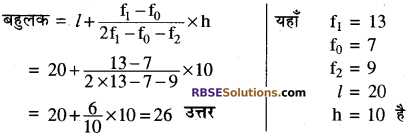
प्रश्न 19.
| वर्ग | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| बारम्बारता | 3 | 15 | 24 | 8 | 5 |
हल:
बारम्बारेता 24 सबसे अधिक है (RBSESolutions.com) अतः बहुलक वर्ग 40-60 होगा।
अतः l = 40, fi = 24, f0 = 15, f2 = 8, h = 20

अतः अभीष्ट बहुलक = 47.2 उत्तर
प्रश्न 20.
समान्तर माध्य की परिभाषा देते हुए इसके किन्हीं (RBSESolutions.com) दो दोषों को बताइए।
हल:
समान्तर माध्य-आँकड़ों में दिए गए चर के योगफल को मानों की संख्या से भाग देकर प्राप्त राशि समान्तर माध्य है। यह औसत भी कहलाती है। अर्थात्
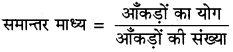
दोष–
- कभी-कभी इसके मान के गणन में ऐसी राशि आ सकती है जो प्रकृति के अनुसार संभव नहीं हो, जैसे परिवार के सदस्यों की संख्या 8.8 या 15.6 होना।
- किसी भी एक मूल्य के नहीं होने पर गणना संभव नहीं है।
प्रश्न 21.
माध्यक की प्रमुख उपयोगिता (RBSESolutions.com) बताइए।
हल:
माध्यक की उपयोगिता–
- यह गुणात्मक विशेषताओं के अध्ययन में श्रेष्ठ है।
- माध्यक ज्ञात करना सरल व सुविधाजनक है। कभी-कभी यह निरीक्षण मात्र से ज्ञात किया जा सकता है।
- इसकी गणना में संपूर्ण आंकड़ों की आवश्यकता नहीं होती है।
- माध्यक सदैव निश्चित एवं स्पष्ट होता है।
- इस पर चरम मानों का प्रभाव नहीं पड़ता, जबकि माध्य में अधिक प्रभाव पड़ता है।
प्रश्न 22.
वर्गीकृत बारम्बारता बंटन से माध्यक ज्ञात करने का सूत्र लिखिए।
हल:
माध्यक \((M)=l+\left(\frac{\frac{N}{2}-C}{f}\right) \times h\)
- l = माध्यक वर्ग निम्न सीमा
- N = कुल बारम्बारता (Ef)
- C = माध्यक वर्ग से पूर्व की संचयी बारम्बारता
- h = माध्यक वर्ग का अन्तराल
- f = माध्यक वर्ग की बारम्बारता
![]()
अन्य महत्त्वपूर्ण प्रश्न
वस्तुनिष्ठ प्रश्न
प्रश्न 1.
बंटने 1, 2, 3, 4, 7, 5, 1 का (RBSESolutions.com) माध्यक है
(क) 4
(ख) 7
(ग) 5
(घ) 3
उत्तर:
(घ) 3
प्रश्न 2.
यदि अग्र बंटन का समान्तर माध्य 5 है, तो P का मान है
| X | 2 | 4 | 6 | P |
| f | 3 | 2 | 1 | 4 |
(क) 8
(ख) 7.5
(ग) 7
(घ) 6.5
उत्तर:
(ख) 7.5
प्रश्न 3.
किसी बारम्बारता बंटन का समान्तर (RBSESolutions.com) माध्य 18.2 है। यदि ∑f = 540 हो तो ∑fx का मान होगा|
(क) \(\frac{540}{18.2}\)
(ख) 18.2 × 540
(ग) 540x
(घ) \(\frac{18.2}{540}\)
उत्तर:
(ख) 18.2 × 540
प्रश्न 4.
यदि 4, 5, 4, n, 5, 5, 4 की समान्तर माध्ये 5 हो तो n का मान होगा
(क) 4
(ख) 5
(ग) 8
(घ) 9
उत्तर:
(ग) 8
प्रश्न 5.
बंटन 1, 9, 4, 5, 11 का माध्यक है
(क) 4
(ख) 5
(ग) 9
(घ) 11
उत्तर:
(ख) 5
प्रश्न 6.
पाँच संख्याओं को माध्य 21 हैं। (RBSESolutions.com) यदि छठवीं संख्या 33 भी उसमें सम्मिलित कर ली जाये तो समस्त संख्याओं को नया माध्य होगा- .
(क) 9
(ख) 18
(ग) 23
(घ) 32
उत्तर:
(ग) 23
प्रश्न 7.
पाँच संख्याओं का माध्य 18 है। यदि एक संख्या हटा दी जाती है, तो माध्य 16 हो जाता है। हटाई गई संख्या है
(क) 10
(ख) 18
(ग) 26
(घ) 16
उत्तर:
(ग) 26
![]()
अतिलघूत्तरात्मक प्रश्न
प्रश्न 1.
एक विद्यालय में कार्यरत प्रधानाध्यापक समेत 5 कर्मचारियों (RBSESolutions.com) का वेतन क्रमशः ₹ 8000, ₹ 5000, ₹ 4000, ₹ 2500, ₹ 1500 मासिक है। विद्यालय में कार्यरत कर्मचारियों का औसत मासिक वेतन ज्ञात कीजिये।
हल:
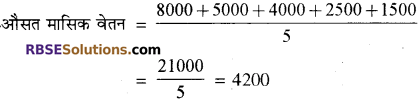
अतः कर्मचारियों का औसत मासिक वेतन = ₹ 4200
प्रश्न 2.
प्रथम दस विषम संख्याओं का समान्तर माध्य ज्ञात कीजिये।
हलं:
प्रथम दस विषम संख्याएँ क्रमशः 1, 3, 5, 7, 11, 13, 15, 17, 19
अतः समान्तर माध्य
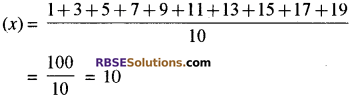
प्रश्न 3.
प्रथम दस सम प्राकृत संख्याओं (RBSESolutions.com) का समान्तर माध्य ज्ञात कीजिए।
हल:
प्रथम दस सम संख्याएँ = 2, 4, 6, 8, 10, 12, 14, 16, 18, 2) हैं।
अत: यात प्राध्य

प्रश्न 4.
बंटन 3, 5, 7, 4, 2, 1, 4, 3, 4 का बहुलक लिखिए।
हल:
उपर्युक्त बंटन में 4 सर्वाधिक 3 बार आया है अतः बहुलक = 4 उत्तर
प्रश्न 5.
निम्न बंटन का माध्यक लिखिए
| X | 5 | 6 | 7 | 8 |
| cf | 2 | 5 | 8 | 10 |
हल:
\(\frac{N}{2}=\frac{10}{2}=5\)
यहाँ 5 संचयी बारम्बारता 5 में आता है जिसका मूल्य 6 है। अतः माध्यक = 6 उत्तर
प्रश्न 6.
निम्न बंटन में P का (RBSESolutions.com) मान लिखिए
| X | 10 | 15 | 20 | 25 | 30 |
| f | 2 | 5 | P | 3 | 2 |
| cf | 2 | 7 | 10 | 13 | 15 |
हल:
10 – 7 = 3 अतः P = 3 उत्तर
![]()
प्रश्न 7.
निम्न तालिका से a का मान लिखिये
| X | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| बारम्बारता f | 2 | 8 | 10 | 13 | 5 | 3 | 1 |
| संचयी बारम्बारता cf | 2 | 10 | 20 | 33 | a | 41 | 42 |
हल:
a = 33 + 5 = 38. उत्तर
प्रश्न 8.
निम्न तालिका से x का (RBSESolutions.com) मान लिखिये
| X | 10 | 20 | 30 | 40 | 50 | 60 |
| f | 2 | 8 | 16 | 26 | 20 | 16 |
| cf | 2 | 10 | X | 52 | 72 | 88 |
उत्तर:
x = 26
प्रश्न 9.
यदि 5, 7, 9, x का समान्तर माध्य 9 हो तो x का मान ज्ञात कीजिए।
उत्तर:
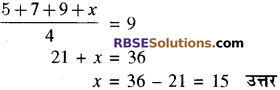
प्रश्न 10.
एक गाँव के 32 परिवारों में उसके सदस्यों की संख्या (RBSESolutions.com) निम्न सारणी के अनुसार है–
| सदस्य संख्या | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| परिवार | 1 | 2 | 4 | 7 | 10 | 3 | 5 |
बंटन का बहुलक लिखिये
उत्तर:
बहुलक = 6
प्रश्न 11.
बहुलक के किसी प्रश्न को हल करने की एक स्थिति निम्न है
![]()
बहुलक वर्ग की बारम्बारता लिखिए।
उत्तर:
15
प्रश्न 12.
प्रथम पाँच सम संख्याओं का समान्तर माध्य (RBSESolutions.com) ज्ञात कीजिए।
हल:
प्रथम पाँच सम संख्यायें निम्न होंगी 2, 4, 6, 8, 10
इन संख्याओं का समान्तर माध्य \(=\frac{2+4+6+8+10}{5}=\frac{30}{5}=6\) उत्तर
![]()
प्रश्न 13.
बंटन 1, 6, 3, 5, 7, 9, 11, 4, 9 का माध्यक तथा बहुलक ज्ञात कीजिए।
हल:
आरोही क्रम में लिखने पर 1, 3, 4, 5, 6, 7, 9, 9, 11 पदों की संख्या = 9 है जो कि विषम संख्या है।
अतः माध्यक \(=\left(\frac{9+1}{2}\right)\) वाँ पद = 5वाँ पद
अतः = 6 उत्तर
दिये गये बंटन में 9 की बारम्बारता 2 है जो कि सबसे अधिक है।
अतः दिये गये बंटन का बहुलक = 9 उत्तर
प्रश्न 14.
निम्न संचयी बारम्बारता बंटन का बहुलक ज्ञात कीजिए–
| X | 1 | 3 | 5 | 7 |
| cf | 2 | 5 | 9 | 12 |
हल:
संचयी बारम्बारता से बारम्बारता सारणी (RBSESolutions.com) तैयार करने पर
| X | 1 | 3 | 5 | 7 |
| f | 2 | 3 | 4 | 3 |
अंक 5 की बारम्बारता 4 है जो कि सबसे अधिक है।
∴ बहुलक = 5 उत्तर
प्रश्न 15.
बंटन 2, 3, 4, 7, 5, 1 का माध्यक ज्ञात कीजिए।
हल:
दिये गये बंटनों को आरोही क्रम में रखने पर 1, 2, 3, 4, 5, 7 पदों की संख्या = 6 है जो कि सम संख्या है।

लघूत्तरात्मक प्रश्न
प्रश्न 1.
यदि x, x + 2, x +4, x + 6, x + 8 का समान्तर माध्य 11 हो तो x का (RBSESolutions.com) मान ज्ञात कीजिए।
हल:
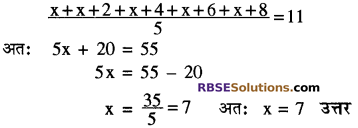
प्रश्न 2.
आठ क्रमागत विषम संख्याओं का औसत 16 है, तो संख्याएँ ज्ञात कीजिये।
हल:
माना कि प्रथम विषम संख्या x है,
अतः क्रमागत आठ विषम संख्याएँ होंगी–
x, x + 2, x + 4, x + 6, x + 8, x + 10, x + 12, x + 14 आठों संख्याओं का औसत
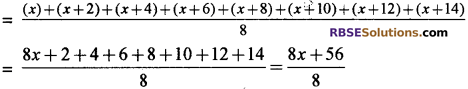
अतः \(\frac{8 x+56}{8}\)
= 16 या 8x + 56 = 128 या x = 9
अत: अभीष्ट क्रमागत विषम संख्याएँ 9, 11, 13, 15, 17, 19, 21, 23
![]()
प्रश्न 3.
बंटन 52, 20, 34, 19, 35, 80, 12, 50, 80 का समान्तर माध्य (RBSESolutions.com) एवं माध्यक ज्ञात कीजिए।
हल:
समान्तर माध्य

माध्यक = 12, 19, 20, 34, 35, 50, 52, 80, 80
माध्यक \(=\frac{n+1}{2}=5\) अतः माध्यक 35 उत्तर
प्रश्न 4.
आरोही क्रम में व्यवस्थित चर मान (x) निम्नानुसार है–
8 11 12 16 16 + x 20 25 30
यदि माध्यक 18 हो तो x का मान ज्ञात कीजिए।
हल:
यहाँ कुल चर मान 8 हैं अत: मध्य में दो पद क्रमशः 16 व 16 +x है।
![]()
या 32 + x = 36 या X = 4
अतः x का मान = 4
निबन्धात्मक प्रश्न
प्रश्न 1.
निम्न बारम्बारता बंटन के लिए समान्तर (RBSESolutions.com) माध्य ज्ञात कीजिए–
| X | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| f | 20 | 43 | 75 | 67 | 72 | 45 | 39 | 9 | 8 | 6 |
हल:
सर्वप्रथम अधिकतम बारम्बारता 72 के संगत चरे मान 25 को कल्पित माध्य A मानकर गणना करेंगे।
A = 25 तथा h = 5
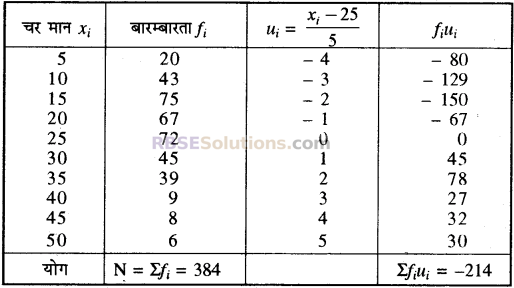
विचलन विधि से समान्तर मध्य
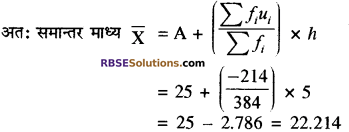
प्रश्न 2.
निम्न बारम्बारता बंटन का पद विचलन विधि से (RBSESolutions.com) समान्तर मध्य ज्ञात कीजिए–
| वर्ग अंतराल | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| बारम्बारत | 10 | 25 | 28 | 12 | 10 | 15 |
हल:
माध्य की गणना
यहाँ A = 65 तथा h = 10
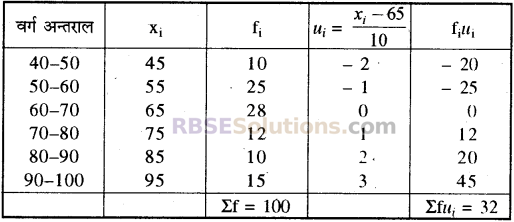
विचलन विधि से समान्तर माध्य
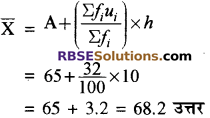
![]()
प्रश्न 3.
नीचे सारणी में कुछ विशेष क्षेत्र के गाँवों की समुद्रतल से ऊँचाई। (RBSESolutions.com) दे रखी है। उस क्षेत्र की समुद्र तल से माध्य ऊँचाई ज्ञात कीजिए।
| ऊँचाई मीटर में | 200 | 600 | 1000 | 1400 | 1800 | 2200 |
| गाँवों की संख्या | 142 | 265 | 560 | 271 | 89 | 16 |
हल:
यहाँ हम A = 1000 तथा h = 400
समान्तर माध्य की गणना सारणी
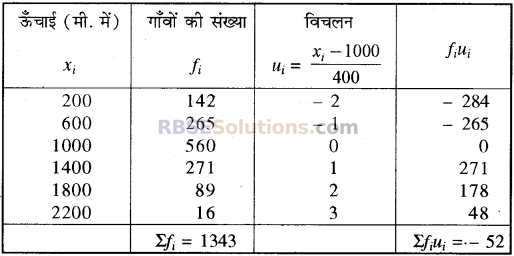
पद विचलन विधि से माध्य

प्रश्न 4.
निम्न समूहित बारम्बारता बंटन का माध्यक (RBSESolutions.com) ज्ञात कीजिए–
| वर्ग अंतराल | 0-8 | 8-16 | 16-24 | 24-32 | 32-40 |
| बारम्बारता | 12 | 20 | 30 | 25 | 13 |
हल:
| वर्ग | बारम्बारता | संचयी बारम्बारता |
| 0-8 | 12 | 12 |
| 8-16 | 20 | 32 |
| 16-24 | 30 | 62 |
| 24-32 | 25 | 87 |
| 32-40 | 13 | 100 |
माध्यक वर्ग = 100/2 = 50 अतः माध्यक वर्ग = (16-24) l = 16, f = 30, C = 32, h = 8

प्रश्न 5.
निम्न बारम्बारता बंटन का माध्यक (RBSESolutions.com) ज्ञात कीजिए
| वर्ग अंतराल | 10-25 | 25-40 | 40-55 | 55-70 | 70-85 | 85-100 |
| बारम्बारता | 6 | 20 | 44 | 26 | 3 | 1 |
हल:
संचयी बारम्बारता सारणी
| वर्ग अंतराल | बारम्बारता (fi) | संचयी बारम्बारता (c.f.) |
| 10-25 | 6 | 6 |
| 25-40 | 20 | 26 |
| 40-55 | 44 | 70 |
| 55-70 | 26 | 96 |
| 70-85 | 3 | 99 |
| 85-100 | 1 | 100 |
| N = 100 |
यहाँN \(\frac{N}{2}=50 \Rightarrow\) माध्यक वर्ग अन्तराल 40-55 है तथा
यहाँ सँगत l = 40, C = 26, h = 15 व f = 44

![]()
अतः माध्यक 48.18 है। उत्तर
![]()
प्रश्न 6.
निम्न बारम्बारता बंटन का बहुलक (RBSESolutions.com) ज्ञात कीजिए
| ऊँचाई (सेमि.) | 50-55 | 55-60 | 60-65 | 65-70 |
| छात्र संख्या | 10 | 20 | 25 | 10 |
हल:
यहाँ सबसे अधिक बारंबारता 25 वर्ग 60-65 की है अतः बहुलक वर्ग = (60-65) है।
अतः l = 60, f1 = 25, f2 = 10, f0 = 20, h = 5

प्रश्न 7.
निम्न बारम्बारता बंटन का बहुलक ज्ञात कीजिए
| वर्ग अंतराल | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
| बारम्बारता | 4 | 3 | 21 | 39 | 19 | 26 |
हल:
यहाँ पर सबसे अधिक बारम्बारता 39 वर्ग 15-20 की है। (RBSESolutions.com) इस प्रकार बहुलक वर्ग = 15-20
पुनः l= 15, f1 = 39, f0 = 21, f2 = 19 तथा h = 5

प्रश्न 8.
निम्न बारम्बारता बंटन के माध्य व माध्यिका (RBSESolutions.com) ज्ञात कीजिए–
| वर्ग | 0-8 | 8-16 | 16-24 | 24-32 | 32-40 | 40-48 |
| fi | 42 | 30 | 50 | 22 | 8 | 5 |
(माध्य. शिक्षा बोर्ड, मॉडल पेपर, 2017-18 )
हल:
सारणी को सही-सही लिखने पर-
| वर्ग अंतराल | बारम्बारता (fi) | मध्यमान (Xi) | fixi |
| 0-8 | 42 | 4 | 168 |
| 8-16 | 30 | 12 | 360 |
| 16-24 | 50 | 20 | 1000 |
| 24-32 | 22 | 28 | 616 |
| 32-40 | 8 | 36 | 288 |
| 40-48 | 5 | 44 | 220 |
| ∑fi = 157 | ∑fiXi = 2652 |
माध्य \(=\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
यहाँ पर ∑fixi = 2652 तथा ∑fi = 157 है।
मान रखने पर माध्य \(=\frac{2652}{157}=16.89\) उत्तर
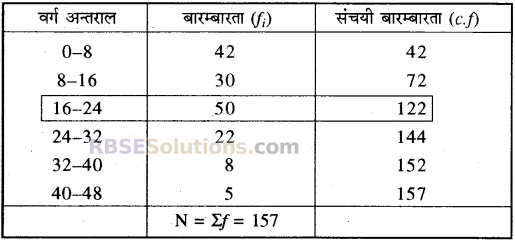
यहाँ \(\frac{N}{2}=\frac{\Sigma f}{2}=\frac{157}{2}=78.5\)
78.5 से बड़ी संचयी बारम्बारता (cf) 122 है, जिसका संगत वर्ग अन्तराल 16-24 है।
अतः l = 16, C = 72, i = 8, f = 50 है।

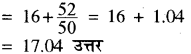
![]()
प्रश्न 9.
निम्न बारम्बारता बंटन के माध्य व बहुलक (RBSESolutions.com) ज्ञात कीजिए
| प्राप्तांक | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| छात्रों की संख्या | 4 | 28 | 42 | 20 | 6 |
(माध्य. शिक्षा बोर्ड, 2018)
हल:
| प्राप्तांक | छात्रों की संख्या (f) | मध्यमान (x) | f.x |
| 20-30 | 4 | 25 | 100 |
| 30-40 | 28 | 35 | 980 |
| 40-50 | 42 | 45 | 1890 |
| 50-60 | 20 | 55 | 1100 |
| 60-70 | 6 | 65 | 390 |
| ∑f = 100 | ∑fx = 4460 |
मध्यमा
\(\begin{aligned} \overline{\mathbf{X}} &=\frac{\sum f x}{\sum f} \\ &=\frac{4460}{100} \\ &=44.60 \end{aligned}\) अंक उत्तर
यहाँ सबसे अधिक (RBSESolutions.com) बारम्बारता 42 समूह (40-50) की है।
अतः l = 40, f1 = 42, f2 = 20, h = 10, f0 = 28

![]()
We hope the RBSE Solutions for Class 10 Maths Chapter 17 केन्द्रीय प्रवृत्ति के माप Additional Questions help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 17 केन्द्रीय प्रवृत्ति के माप Additional Questions, drop a comment below and we will get back to you at the earliest.