RBSE Solutions for Class 6 Maths Chapter 13 Ratio and Proportion Ex 13.1 is part of RBSE Solutions for Class 6 Maths. Here we have given Rajasthan Board RBSE Class 6 Maths Chapter 13 Ratio and Proportion Exercise 13.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 6 |
| Subject | Maths |
| Chapter | Chapter 13 |
| Chapter Name | Ratio and Proportion |
| Exercise | Ex 13.1 |
| Number of Questions | 12 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 6 Maths Chapter 13 Ratio and Proportion Ex 13.1
Question 1.
A social Awareness camp was organized in the summer (RBSESolutions.com) vacations this year. 25 girls and 15 boys participate in the camp and put water bowl for birds.
(i) What is the ratio of number of girls to the number of boys ?
(ii) What is the ratio of number of girls to the number of participants ?
Solution:
Number of girls = 25
Number of boys = 15
Total numbers = 25 + 15 = 40
(i) The ratio of number of girls to the number of boys
Required ratio = \(\frac { 25 }{ 15 } \) = \(\frac { 5 }{ 3 } \) = 5 : 3
(ii) Required ratio = \(\frac { 25 }{ 40 } \) = \(\frac { 5 }{ 8 } \) = 5 : 8
![]()
Question 2.
During a Tree Plantation programme in a school, students of 6th Class (RBSESolutions.com) planted 8 Neem trees, 13 mango trees and 19 Guava trees.
(i) What is the ratio of number of Neem trees planted to the number of Mango tress planted ?
(ii) What is the ratio of total number of tress planted to the number of Neem trees planted ?
Solution:
Neem trees = 8
Mango trees = 13
Guava trees = 19
Total trees = 8 + 13 + 19 = 40
(i) Required ratio = \(\frac { 8 }{ 13 } \) = 8 : 13
(ii) Required ratio = \(\frac { 40 }{ 8 } \) = 5 : 1
Question 3.
See the figure and find (RBSESolutions.com) the ratio of :
(i) Number of triangles to the number of circles.
(ii) Number of square to all the figures.
(iii) Number of triangles to all the figures.
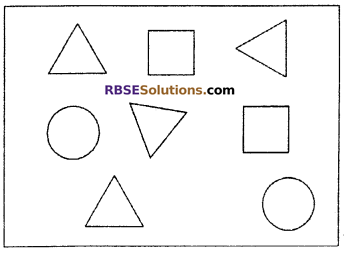
Solution:
In figure,
Number of triangles = 4
Number of circles = 2
Number of squares = 2
Total figures = 4 + 2 + 2 = 8
(i) Number of triangles to (RBSESolutions.com) the number of circle,
Required ratio = \(\frac { 4 }{ 2 } \) = \(\frac { 2 }{ 1 } \) = 2 : 1
(ii) Number of squares to all the figures,
Required ratio = \(\frac { 2 }{ 8 } \) = \(\frac { 1 }{ 4 } \) = 1 : 4
(iii) Number of triangles to all the figures.
Required ratio = \(\frac { 4 }{ 8 } \) = \(\frac { 1 }{ 2 } \) = 1 : 2
Question 4.
Fill in the following (RBSESolutions.com) blanks
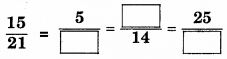
Solution:

Question 5.
Find the ratio of (RBSESolutions.com) the following
(i) 25 to 150
(ii) 72 to 36
(iii) 55 km to 121 km
(iv) 35 minute to 55 minute
Sol.
(i) Required ratio = \(\frac { 25 }{ 150 } \) = \(\frac { 1 }{ 6 } \) = 1 : 6
(ii)Required ratio = \(\frac { 72 }{ 36 } \) = \(\frac { 2 }{ 1 } \) = 2 : 1
(iii) Required ratio = \(\frac { 55 }{ 121 } \) = \(\frac { 5 }{ 11 } \) = 5 : 11
(iv) Required ratio = \(\frac { 35 }{ 55 } \) = \(\frac { 7 }{ 11 } \) = 7 : 11
![]()
Question 6.
Find the ratio (RBSESolutions.com) of the following
(i) 60 paise and 3 Rupees
(ii) 800 gm and 5 kg
(iii) 15 minute and 1 hour
(iv) 1 litre and 750 ml.
Solution:

Question 7.
During a year, a cowshed had received donations (RBSESolutions.com) worth Rs. 3,25,000 out of which Rs. 3,00,000 were spend on the welfare of the cows. Find the ratio of donations received to the expenditure incurred.
Solution:
cowshed had received donations in a year = 3,25,000
Donation received in a year = Rs. 3,00,000
Required ratio = \(\frac { 3,25,000 }{ 3,00,000 } \) = \(\frac { 325 }{ 300 } \)
⇒ \(\frac { 25\times 13 }{ 25\times 12 } \) = \(\frac { 13 }{ 12 } \) = 13 : 12
Question 8.
Mahesh studies 4 hours and Laxmi studies 180 minutes daily. Find the ratio of (RBSESolutions.com) study time of Mahesh to study time of Laxmi. (1 hour = 60 minutes).
Solution:
Mahesh studies everyday = 4 hours
Laxmi studies everyday 180 minutes

Question 9.
Out of 720 student in a school, 360 students stay (RBSESolutions.com) at a hostel. Find the ratio of number of student staying at the hostel to the total number of students.
Solution:
Total students = 720
Students stays at hostel = 360
Required ratio = \(\frac { 360 }{ 720 } \) = \(\frac { 1 }{ 2 } \) = 1 : 2
Question 10.
Talisma and Gurumit started a business and invested (RBSESolutions.com) money in the ratio 2 : 5. After one year the total profit was Rs. 35,000. Find the shares of profit for Talsima and Gurumit.
Solution:
Sum of given ratios = 2 + 5 = 7
Total profit = Rs. 35,000
Talisma’s share = \(\frac { 2 }{ 7 } \) x 35,000 = Rs. 10,000
Gurumit’s share = \(\frac { 5 }{ 7 } \) x 35,000= Rs. 25,000
![]()
Question 11.
Consider the statement : Ratio of breadth and length of hall is 3:4 Complete the (RBSESolutions.com) following table that show some possible breadths and lengths of the hall.

Solution:

\(\frac { 25\times 13 }{ 25\times 12 } \) = \(\frac { 36 }{ 48 } \)
Thus
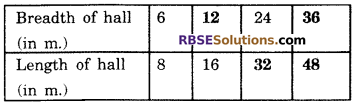
Question 12.
Present age of father is 45 years and (RBSESolutions.com) that of his son is 15 years. Find the ratio of
(i) Present age of father of the present age of son.
(ii) Age of father to the age to son, when son was 10 years old.
(iii) Age of father after 5 years to the age of son after 5 years.
(iv) Age of father to the age of son, when father will be 60 years old.
Solution:
Present age of father = 45 years
Present age of son = 15 years
(i) Required ratio = \(\frac { 45 }{ 15 } \) = \(\frac { 3 }{ 1 } \) = 3 : 1
(ii) 5 years ago (when son was 10 years old) age of father = 45 – 5 = 40 years
and age of son = 15 – 5 = 10 years
Required ratio = \(\frac { 40 }{ 10 } \) = \(\frac { 4 }{ 1 } \) = 4 : 1
(iii) After 5 years, age of (RBSESolutions.com) father = 45 + 5 = 50 years
and, age of son = 15 + 5 = 20 years
Required ratio = \(\frac { 50 }{ 20 } \) = \(\frac { 5 }{ 2 } \) = 5 : 2
(iv) when father will be 60 years old (i.e. after 15 years)
age of son = 15 + 15 = 30 years
Required ratio = \(\frac { 60 }{ 30 } \) = \(\frac { 2 }{ 1 } \) = 2 : 1
![]()
We hope the RBSE Solutions for Class 6 Maths Chapter 13 Ratio and Proportion Ex 13.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 6 Maths Chapter 13 Ratio and Proportion Exercise 13.1, drop a comment below and we will get back to you at the earliest.