Rajasthan Board RBSE Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.3
Question 1.
Prove that
\({ sin }^{ 2 }\frac { \pi }{ 6 } +{ cos }^{ 2 }\frac { \pi }{ 3 } -tan^{ 2 }\frac { \pi }{ 4 } =-\frac { 1 }{ 2 } \).
Solution:
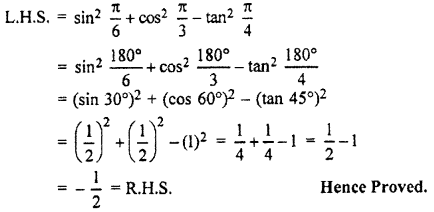
Question 2.
\({ sin }^{ 2 }\frac { \pi }{ 6 } +{ cosec }^{ 2 }\frac { 7\pi }{ 6 } -cos^{ 2 }\frac { \pi }{ 3 } =\frac { 3 }{ 2 } \).
Solution:
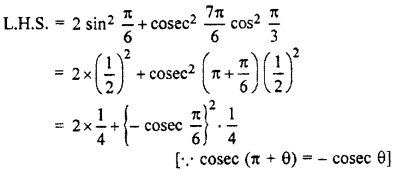
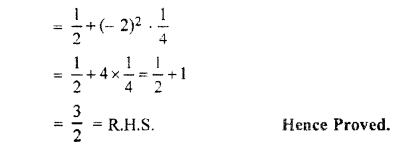
Question 3.
\({ cot }^{ 2 }\frac { \pi }{ 6 } +{ cosec }^{ 2 }\frac { 5\pi }{ 6 } +3tan^{ 2 }\frac { \pi }{ 6 } =6 \).
Solution:
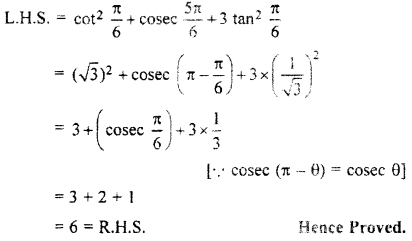
Question 4.
\(2{ sin }^{ 2 }\frac { 3\pi }{ 4 } +2{ cos }^{ 2 }\frac { \pi }{ 4 } +2sec^{ 2 }\frac { \pi }{ 3 } =10\).
Solution:
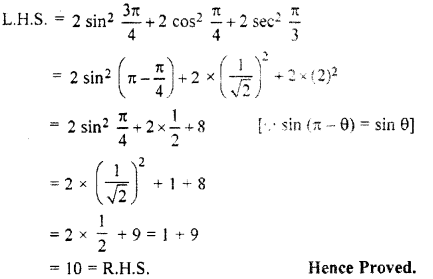
Question 5.
Find the value of :
(i) sin 75°
(ii) tan 15°
Solution :
(i) sin 75° = sin (45° + 30°)
= sin 45°.cos 30° + cos 45°.sin 30°
(∵ sin (A + B) = sin A cos B + cos A sin B)
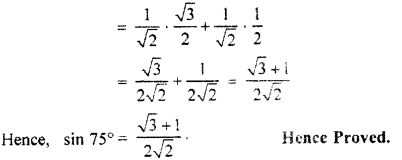

Question 6.
Prove that:
tan 225° cot 405° + tan 765° cot 675° = 0.
Solution :
L.H.S.
= tan 225° cot 405° + tan 765° cot 675°
= tan (360° – 135°) cot (360° + 45°) + tan (2 × 360° + 45°) cot (2 × 360° – 45°)
= (- tan 135°) (cot 45°) + (tan 45°) (- cot 45°)
= – tan 135° cot 45° – tan 45° cot 45°
= – tan (180° – 45°) cot 45° – tan 45° cot 45°
= – (- tan 45°) cot 45° – tan 45° cot 45°
= tan 45° cot 45° – tan 45° cot 45° = 0
= R.H.S.
Hence Proved.
Question 7.
![]()
Solution:
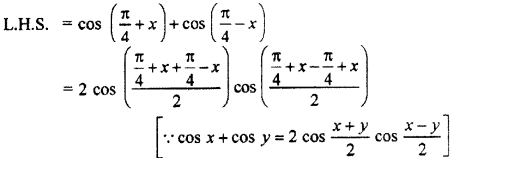

Question 8.
![]()
Solution:
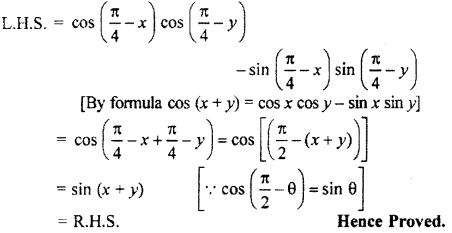
Question 9.
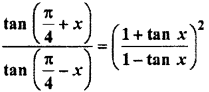
Solution:
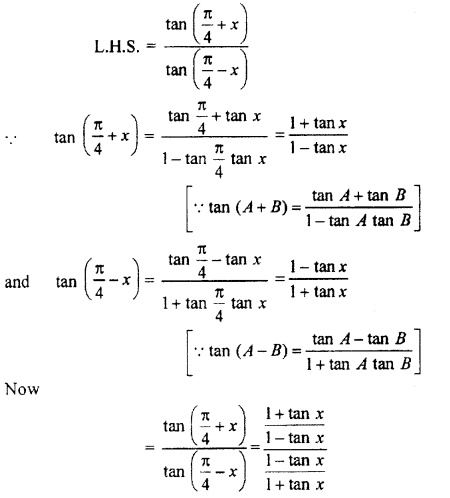
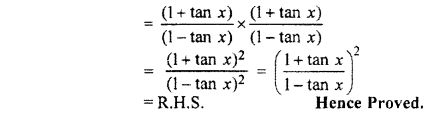
Question 10.
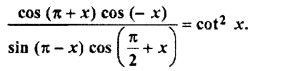
Solution:
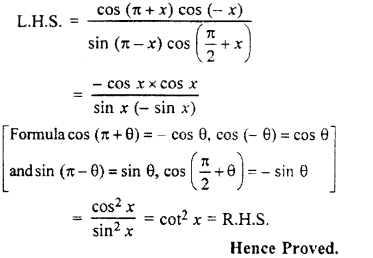
Question 11.
sin (n + 1) x sin (n + 2)x + cos (n + 1)x cos (n + 2)x = cos x
Solution :
L.H.S.
= sin (n + 1)x sin (n + 2)x + cos (n + 1)x cos (n + 2)x
= cos (n + 1)x cos (n + 2)x + sin (n + 1)x × sin (n + 2)x
[Formula cos (x – y) – cos x cos y + sin x sin y]
= cos [(n + 1)x – (n + 2)x]
= cos [nx + x – nx – 2x]
= cos (- x) cos x = R.H.S.
Hence Proved.
Question 12.
sin2 6x – sin2 4x = sin 2x sin 10x.
Solution :
L.H.S. = sin2 6x – sin2 4x
= \(\frac { 1 }{ 2 }\) [2 sin2 6x – 2sin2 4x] [Multiply and divide by 2]
= \(\frac { 1 }{ 2 }\) [(1 – cos 12x) – (1 – cos 8x)]
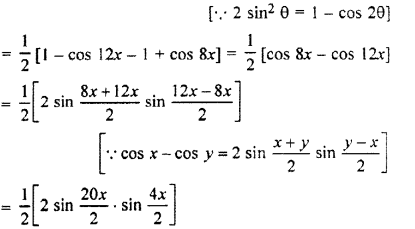
= sin 10x sin 2x =sin 2x sin 10x = R.H.S.
Second Method: R.H.S.
= sin2 6x – sin2 4x
= (sin 6x + sin 4x) (sin 6x – sin 4x)
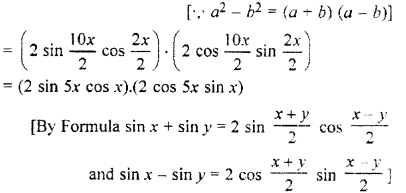
= (2 sin 5x cos 5x).(2 sin x cos x)
= sin 10x.sin 2x [∵ sin 2θ = 2 sin θ cos θ]
= sin 2x sin 10x = R.H.S. Hence Proved.
Question 13.
sin 2x + 2 sin 4x + sin 6x = 4 cos2 x sin 4x.
Solution :
L.H.S. = sin 2x + 2 sin 4x + sin 6x
= (sin 2x + sin 6x) + 2 sin 4x
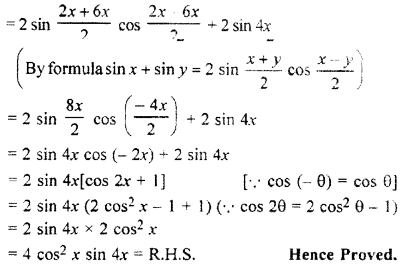
Question 14.
cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
Solution :
L.H.S. = cot 4x (sin 5x + sin 3x)

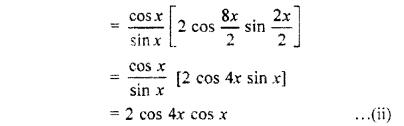
From (i) and (ii), we get
cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x).
L.H.S. = R.H.S.
Hence Proved.
Question 15.
![]()
Solution:
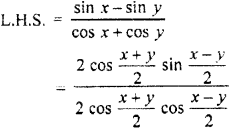
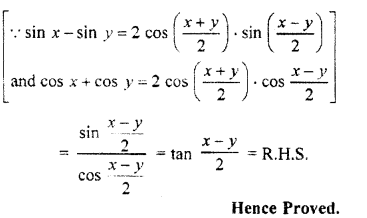
Question 16.
![]()
Solution:
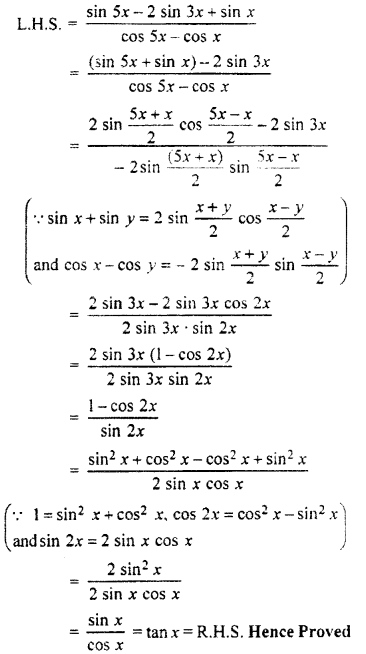
Question 17.
![]()
Solution:
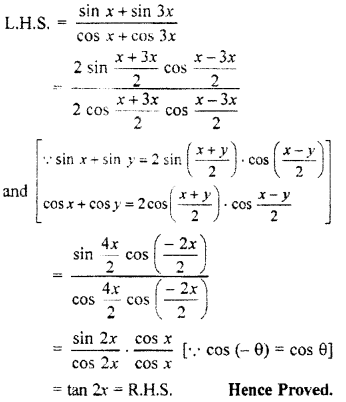
Question 18.
![]()
Solution:
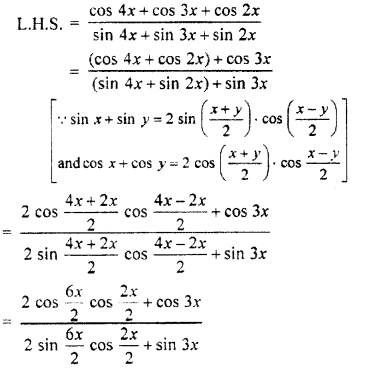
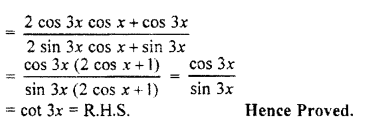
Question 19.
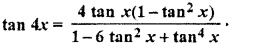
Solution:

Question 20.
cos 4x = 1 – 8 sin2 x cos2 x.
Solution :
L.H.S. = cos 4x = cos 2(2x)
(cos θ = 1 – 2 sin2 θ)
= 1 – 2 sin2 2x
= 1 – 2 (2 sin x cos x)2 [∵ sin 2x = 2 sin x cos x]
= 1 – 2 x 4 sin2 x cos2 x
= 1 – 8 sin2 x cos2 x = R.H.S.
Hence Proved.
Question 21.
cos 6x = 32 cos6 x- 48 cos4 x + 18 cos2 x- 1.
Solution :
L.H.S. = cos 6x = cos 3(2x) [∵ cos 3x = 4 cos3 x – 3 cos x]
= 4 cos3 2x – 3 cos 2x
= cos 2x (4 cos2 2x – 3)
= cos 2x [4(cos 2x)2 – 3] [∵ cos 2x = 2 cos2 x – 1]
= cos 2x [4(2 cos2 x – l)2 – 3]
= cos 2x [4(4 cos4 x + 1 – 4 cos2 x) – 3]
= cos 2x (16 cos4 x + 4 – 16 cos2 x – 3)
= (2 cos2 x – 1) (16 cos4 x + 4 – 16 cos2 x – 3)
= 32 cos6 x + 8 cos2 x – 32 cos4 x – 6 cos2 x – 16 cos4 x – 4 + 16 cos2 x + 3
= 32 cos6 x – 48 cos4 x + 18 cos2 x – 1
= R.H.S. Hence Proved.
Question 22.
[1 + cot θ – sec (θ + π/(2)]
[1 + cot θ + sec (θ + π/(2)] = 2 cot θ
Solution :
L.H.S.
[1 + cot θ – sec (θ + π/(2)]
[1 + cot θ + sec (θ + π/(2)]
= [1 + cot θ + cosec θ] [1+ cot θ – cosec θ]
= (1 + cot)2 – cosec2θ
= 1 + cot2θ + 2 cotθ – cosec2θ
= 1 + 2 cot θ – (cosec2θ – cot2θ)
= 1+2 cot θ – 1
= 2 cot θ = R.H.S.
Hence Proved.
RBSE Solutions for Class 11 Maths